LeetCode 407. Trapping Rain Water II

最新推荐文章于 2022-07-20 17:34:52 发布

原创最新推荐文章于 2022-07-20 17:34:52 发布 · 272 阅读

0 ·

CC 4.0 BY-SA版权

leetcode 专栏收录该内容

414 篇文章

订阅专栏

本文介绍了一种利用最小堆解决二维地图中雨水收集问题的方法。通过遍历边界并将内部单元格与周围较高单元格比较，逐步填充内部区域，计算总的积水体积。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.

Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.

Example:

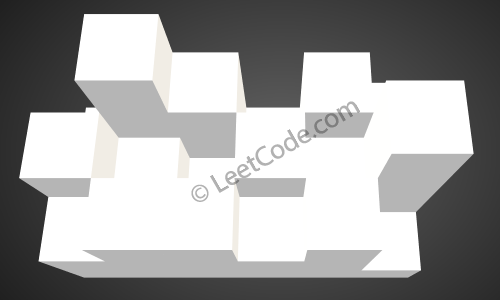The above image represents the elevation map [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.

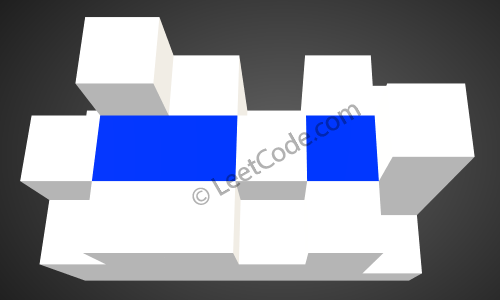
After the rain, water is trapped between the blocks. The total volume of water trapped is 4.

使用min—heap的方式进行处理，可以非常好的解决这个问题。

java

class Cell {
    int x;
    int y;
    int z;
    public Cell(int x, int y, int z) {
        this.x = x;
        this.y = y;
        this.z = z;
    }
}
public class Solution {
    public int trapRainWater(int[][] arr) {
        if (arr == null || arr.length == 0 || arr[0] == null || arr[0].length == 0) {
            return 0;
        }
        Comparator<Cell> cmp = new Comparator<Cell>() {
            public int compare(Cell c1, Cell c2) {
                return c1.z - c2.z;
            }
        };
        PriorityQueue<Cell> heap = new PriorityQueue<>(1, cmp);
        boolean[][] visit = new boolean[arr.length][arr[0].length];
        for (int i = 0; i < arr.length; i++) {
            heap.offer(new Cell(i, 0, arr[i][0]));
            heap.offer(new Cell(i, arr[0].length - 1, arr[i][arr[0].length - 1]));
            visit[i][0] = true;
            visit[i][arr[0].length - 1] = true;
        }
        for (int i = 0; i < arr[0].length; i++) {
            heap.offer(new Cell(0, i, arr[0][i]));
            heap.offer(new Cell(arr.length - 1, i, arr[arr.length - 1][i]));
            visit[0][i] = true;
            visit[arr.length - 1][i] = true;
        }
        int res = 0;
        int[] dir_x = new int[] {0, 0, 1, -1};
        int[] dir_y = new int[] {1, -1, 0, 0};
        while (!heap.isEmpty()) {
            Cell cell = heap.poll();
            for (int i = 0; i < 4; i++) {
                int n_x = cell.x + dir_x[i];
                int n_y = cell.y + dir_y[i];
                if (n_x >= 0 && n_x < arr.length && n_y >= 0 && n_y < arr[0].length && !visit[n_x][n_y]) {
                    heap.offer(new Cell(n_x, n_y, Math.max(cell.z, arr[n_x][n_y])));
                    visit[n_x][n_y] = true;
                    res += Math.max(0, cell.z - arr[n_x][n_y]);
                }
            }
        }
        return res;
    }
}