统计学入门

统计学入门

目的：数据分析的工作，需要学习统计学的基础课程；

我想要的目的：统计学中在数据分析中用到知识和概念，最好有落地的方法论已做指导；

哈里斯堡社区大学公开课：统计学入门

http://open.163.com/special/opencourse/statistics.html

1.笔记：

1.统计学分为2枝，描述性统计学和推断性统计学；
描述性统计学：收集和报告（描述和总结）
推断性统计学（建立在样本之上）：收集样本，特征观察，根据样本做出推断
数据中的参数：分为定性（类似于描述）和定量（数字描述）
定量变量分为2部分：离散随机变量和连续的随机变量（往往是测量结果）

 

可汗学院：统计学

http://open.163.com/movie/2017/8/6/O/MCU0FC1GD_MCU0GUS6O.html

笔记：(目前大多涉及数据统计方法)

均值：数据之和除以数据个数的结果
中位数：数据排序后，处于中间的数据，奇数个数去中间，偶数个数是中间2个数的均值
众数：出现次数最多的数据
极差：最大值与最小值的差；
中程树：最大值与最小值的均值
象形统计图是象形图像表示统计数据的图像；
条形图：分类汇总数据
线形图：表示趋势
饼图：表示占比
图形误导:图形刻度
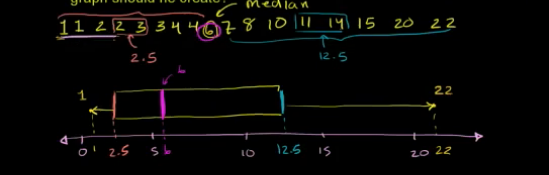
茎叶图：是将数组中的数按照位数进行比较，分别做茎和叶，以此做数据统计；

盒须图：展示数据分布，同时可显示中位数，极差等等数据；

 
描述统计学：
集中趋势：描述数据的特定数值；
均值--算数平均数
离群值--特殊数据
样本：
总体：

在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。
为避免出现离均差总和为零，离均差平方和受样本含量的影响，
举例：
1，2，3，4，5，6，7
平均值：4
方差：[(1-4)^2+(2-4)^2+(3-4)^2+(4-4)^2+(5-4)^2+(6-4)^2+(7-4)^2]/7=4
统计学采用平均离均差平方和来描述变量的变异程度。
总体方差：方差用来表述数据和均值之间的偏离程度，总体方差的计算公式是σ2=Σ(Xi-μ)2/N，
其中求和的i从1到N。
样本方差：样本方差不同于总体方差，
计算公式为S2=Σ(Xi-μ)2/(n-1)，其中求和的i从1到n，
这里方差用的是n-1而不是n。
标准差：标准差σ是表述数据和均值之间的偏离程度的另一个重要标志。
它等于方差的平方根。
例子：
“标准差”(standard deviation)也称“标准偏差”，它可以通过计算方差的算术平方根来求得。标准差表征了各数据偏离平均值的距离，它反映出一个数据集的离散程度。

计算标准差的步骤通常有四步：
（1）计算平均值
（2）计算方差
（3）计算平均方差
（4）计算标准差

例如，对于一个有六个数的数集2,3,4,5,6,8，其标准差可通过以下步骤计算：

（1）计算平均值：
(2 + 3 + 4 + 5+ 6 + 7+4)/6 = 24/6 = 4

（2）计算方差：
(2 – 5)^2 = (-3)^2= 9
(3 – 5)^2 = (-2)^2= 4
(4 – 5)^2 = (-1)^2= 0
(5 – 5)^2 = 0^2= 0
(6 – 5)^2 = 1^2= 1
(8 – 5)^2 = 3^2= 9

（3）计算平均方差：
(9 + 4 + 0 + 0+ 1 + 9)/6 = 24/6 = 4

（4）计算标准差：
√4 = 2
随机变量：随机变量是表示随机现象各种结果的变量。
萨尔曼认为随机变量并不是传统意义上的变量，
而是一种由随机过程映射到数值的函数。
例如：骰子抛出的数值就是随机变量；
分为：离散的和连续的
连续随机变量：连续型随机变量是指如果随机变量X的所有可能取值不可以逐个列举出来，
而是取数轴上某一区间内的任一点的随机变量。
当随机变量的可取值全体为一离散集时称其为离散型随机变量
概率密度函数：概率密度函数的概念。求概率也就是对概率密度函数进行积分。