数据预处理

复习笔记

• 现实数据的缺陷：不完整、含噪声、编码不一致
• 数据预处理的任务
  
  • 数据清理：空缺值，噪声数据，删除孤立点，解决不一致性
  • 数据集成：集成多个数据库、数据立方体或文件
  • 数据归约：得到数据集的压缩表示，但可以得到相同或相近的结果
  • 数据变换：规范化和聚集
  • 数据离散化：将连续数据进行离散处理

---

数据清理

处理缺失值

• 忽略元组
• 人工填写
• 全局值填充（如0，-∞）
• 其属性的平均值填充
• 与给定元组属同一类的所有样本的平均值填充
• 推测最可能的值（如判定树）

处理噪声数据

• 分箱(binning)
• 聚类：（监测并且去除孤立点）
• 回归

数据集成

将多个数据源中的数据整合到一个一致的存储中，减少或避免结果数据中的冗余与不一致性，从而可以提高挖掘的速度和质量

冗余数据处理

• 相关分析（数值型数据）
  
  • 协方差（Covariance）
    衡量两个变量的变化趋势是否一致
    
  • 相关系数（皮尔逊相关系数）
    （）
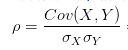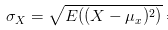  • 卡方检验（χ2 (chi-square test）
    统计样本的实际观测值与理论推断值之间的偏离程度；卡方值越小，偏差越小，越趋于符合；两个值完全相等时，卡方值就为0，表明理论值完全符合。
    
    自由度: $(c-1)*(r-1)$

数据归约

用来得到数据集的归约表示，比原数据规模小，但可以产生或几乎相同的分析结果

• 维归约

  • 小波分析
    保存小波较大的系数进行原始数据的压缩，主要用于图像分析中
  • PCA（Principal component analysis）/K-L变换
    找到一个投影，其能表示数据的最大变化
  • 特征筛选
    通过删除不相干的属性或维减少数据量
    
    • 信息熵：刻画系统的混乱程度
      
    • 条件信息熵：刻画在已知X的基础上需要多少信息来描述Y
      
    • 信息增益：刻画在已知X的基础上需要节约多少信息来描述Y
      $IG(Y|X) = H(Y) – H(Y|X)$

• 数量归约：通过选择替代的、较小的数据表示形式来减少数据量

  • 直方图
    将某属性的数据划分为不相交的子集或桶，桶中放置该值的出现频率
  • 聚类
    将数据集划分为聚类，然后通过聚类来表示数据集
  • 抽样
    用数据的较小随机样本（子集）表示大的数据集
  • 数据立方体聚集
• 数据压缩
  
  • 有损压缩（如字符串压缩）
  • 无损压缩（如音频/视频压缩）

数据变换

• 最小－最大规范化
  
• 连续数据离散化
  通过将属性域划分为区间，减少给定连续属性值的个数。区间的标号可以代替实际的数据值
• 概念分层
  通过使用高层的概念（比如：青年、中年、老年）来替代底层的属性值（比如：实际的年龄数据值）来规约数据