如有需要,联系更新。
原文链接: https://www.sciencedirect.com/science/article/pii/S1361841512000977
matlab版代码:https://github.com/JojoWong9128/ConfidenceMapC-Test
(说明:该代码仅为验证C++代码每一步的准确度,为C++版本代码的逐步对照实现,运行速度不在考虑范围。)
算法概述
算法主要是为了解决超声图像的衰减和声影对医学影像的后期计算造成影响这一问题,通过计算每个像素点的confidence来由此反映出其对应的不确定性。文献的创新点在于利用超声图像的特定约束条件借助随机游走算法框架对整个confidence估计进行建模。
算法步骤
Step1 输入超声图像I0;
Step2 计算衰减后的intensity,I;
Step3 标记种子点并对种子点赋值;
Step4 计算邻接矩阵、度矩阵和拉普拉斯矩阵,L;
Step5 将L分块
其中L_m为marked区域的L,L_u为unmarked区域的L;
Step6 求解
其中,X_m即为种子点(marked)的值。
最终求得的X_u即为unmarked区域的confidence map值。
纵观全文,笔者有以下几点自问自答,在此给出,如若刚巧被了解此文算法的你看到,希望可以一起交流学习。
Q1、文献所说的ultrasound specific constraints指的是什么?用于模型的何处?
A1、 ① transmission modeling
② depth dependent attenuation
③ ultrasound scanline
“超声传递模型”“依赖于深度的衰减”“超声扫描线”三个关键词按指超声在传递的过程中会有衰减,算法有用到沿scanline方向的能量衰减模型。
Q2、最终的求解公式中X_m是什么?由何而来?为什么?
A2、要弄清楚这个问题,首先要明白marked和unmarked分别对应的是什么。marked也即文中所说的seeds,文中有“the seeds are automatically placed at the beginning of each scanline,representing the position of the virtual transducer elements”每条scanline的起始点像素为种子点(marked 点) "and at the end of each scanline,representing the absorption region after which no signal is practically recorded" 每条scanline的最后一个像素点为种子点,再往深处不再有像素被记录。暗示,每条scanline的起始点像素的confidence若为1,则scanline的最后一个像素点的confidence为0,这就是所谓的X_m,除此之外,整幅图像的边界函数由此出现(狄利克雷边界条件)。既然提到狄利克雷边界条件,那么必然还有文章,此处暂且不谈。
Q3、L如何计算?又是如何进行分块的?
A3、L,即拉普拉斯矩阵,图论中对图(graph)的一种记录方式。该文构建的为无向图。
L = D - A
其中,A为所构建的图的邻接矩阵(点与点是否相连,若相连权重多少的表征矩阵),D为度矩阵,是一个对角阵,对角线上的元素为A矩阵的对应列(或对应行,无向图中的A为对称阵)所有元素的和(博文中不好打公式,原谅纯文字描述……)。











 本文介绍了一种解决超声图像衰减和声影问题的算法,通过计算每个像素点的置信度反映其不确定性。算法利用随机游走框架,并结合超声图像的特定约束条件,最终求解得到未标记区域的置信度地图。
本文介绍了一种解决超声图像衰减和声影问题的算法,通过计算每个像素点的置信度反映其不确定性。算法利用随机游走框架,并结合超声图像的特定约束条件,最终求解得到未标记区域的置信度地图。
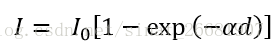
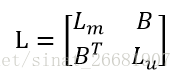
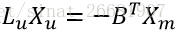
















 862
862

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








