机器学习入门一

# 机器学习入门一
安装环境省略。。。
背景：
这个数据集是基于 1990 年加州普查的数据。数据已经有点老（1990 年还能买一个湾区不错的房子），但是它有许多 优点，利于学习，所以假设这个数据为最近的。
你的第一个任务是利用加州普查数据，建立一个加州房价模 型。这个数据包含每个街区组的人口、收入中位数、房价中位数等指标。 街区组是美国调查局发布样本数据的最小地理单位（一个街区通常有 600 到 3000 人）。我 们将其简称为“街区”。 你的模型要利用这个数据进行学习，然后根据其它指标，预测任何街区的的房价中位数。

1.0 加载数据，也可从网上直接load,方式很多

def load_housing_data():
return pd.read_csv(‘housing.csv’)
housing=load_housing_data()

2.0 对数据的描述

print housing.head()

print housing.describe()


count 、 mean 、 min 和 max 几行的意思很明显了。注意，空值被忽略了（所以，卧室总数 是 20433 而不是 20640）。 std 是标准差（揭示数值的分散度）。25%、50%、75% 展示了 对应的分位数：每个分位数指明小于这个值，且指定分组的百分比。例如，25% 的街区的房 屋年龄中位数小于 18，而 50% 的小于 29，75% 的小于 37。这些值通常称为第 25 个百分位 数（或第一个四分位数），中位数，第 75 个百分位数（第三个四分位数）。
housing.hist(bins=50,figsize=(20,15))
另一种快速了解数据类型的方法是画出每个数值属性的柱状图。柱状图（的纵轴）展示了特 定范围的实例的个数。你还可以一次给一个属性画图，或对完整数据集调用 hist() 方法，后 者会画出每个数值属性的柱状图。例如，你可以看到略微超过 800 个街区 的 median_house_value 值差不多等于 500000 美元。

注意柱状图中的一些点：
1. 首先，收入中位数貌似不是美元（USD）。与数据采集团队交流之后，你被告知数据是 经过缩放调整的，过高收入中位数的会变为 15（实际为 15.0001），过低的会变为 5（实际为 0.4999）。在机器学习中对数据进行预处理很正常，这不一定是个问题，但你 要明白数据是如何计算出来的。
2. 房屋年龄中位数和房屋价值中位数也被设了上限。后者可能是个严重的问题，因为它是 你的目标属性（你的标签）。你的机器学习算法可能学习到价格不会超出这个界限。你 需要与下游团队核实，这是否会成为问题。如果他们告诉你他们需要明确的预测值，即 使超过 500000 美元，你则有两个选项： i. 对于设了上限的标签，重新收集合适的标签； ii. 将这些街区从训练集移除（也从测试集移除，因为若房价超出 500000 美元，你的系 统就会被差评）。

3. 3.0对数据分割测试集，训练集

在这个阶段就分割数据，听起来很奇怪。毕竟，你只是简单快速地查看了数据而已，你需要 再仔细调查下数据以决定使用什么算法。这么想是对的，但是人类的大脑是一个神奇的发现 规律的系统，这意味着大脑非常容易发生过拟合：如果你查看了测试集，就会不经意地按照 测试集中的规律来选择某个特定的机器学习模型。再当你使用测试集来评估误差率时，就会 导致评估过于乐观，而实际部署的系统表现就会差。这称为数据透视偏差。 理论上，创建测试集很简单：只要随机挑选一些实例，一般是数据集的 20%，放到一边。

方法1.0

def split_train_test(data,test_ratio):
shuffled_indices=np.random.permutation(len(data))
test_set_size=int(len(data)*test_ratio)
test_indices=shuffled_indices[:test_set_size]
train_indices=shuffled_indices[test_set_size:]
return data.iloc[train_indices],data.iloc[test_indices]
#train_set,test_set = split_train_test(housing,0.2)
#print len(housing),len(train_set),len(test_set)
这个方法可行，但是并不完美：如果再次运行程序，就会产生一个不同的测试集！多次运行 之后，你（或你的机器学习算法）就会得到整个数据集，这是需要避免的。 解决的办法之一是保存第一次运行得到的测试集，并在随后的过程加载。另一种方法是在调 用 np.random.permutation() 之前，设置随机数生成器的种子（比如 np.random.seed(42) ）， 以产生总是相同的洗牌指数（shuffled indices）。 但是如果数据集更新，这两个方法都会失效。一个通常的解决办法是使用每个实例的ID来判 定这个实例是否应该放入测试集（假设每个实例都有唯一并且不变的ID）。例如，你可以计 算出每个实例ID的哈希值，只保留其最后一个字节，如果该值小于等于 51（约为 256 的 20%），就将其放入测试集。这样可以保证在多次运行中，测试集保持不变，即使更新了数 据集。新的测试集会包含新实例中的 20%，但不会有之前位于训练集的实例。下面是一种可 用的方法：
注：不要问为什么是42，不是其他，哲学问题
def test_set_check(identifier,test_ratio,hash):
return hash(np.int64(identifier)).digest()[-1] < 256 * test_ratio
def split_train_test_by_id(data,test_ratio,id_column,hash=hashlib.md5):
ids = data[id_column]
in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio, hash))
print in_test_set.value_counts()
return data.loc[~in_test_set], data.loc[in_test_set]

如果使用行索引作为唯一识别码，你需要保证新数据都放到现有数据的尾部，且没有行被删 除。如果做不到，则可以用最稳定的特征来创建唯一识别码。例如，一个区的维度和经度在 几百万年之内是不变的，所以可以将两者结合成一个 ID：
##add index
#housing_with_id = housing.reset_index() # adds an index column
#train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, “index”)
#housing_with_id[“id”] = housing[“longitude”] * 1000 + housing[“latitude”]
#train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, “id”)
#print len(housing),len(train_set),len(test_set)
目前为止，我们采用的都是纯随机的取样方法。当你的数据集很大时（尤其是和属性数相 比），这通常可行；但如果数据集不大，就会有采样偏差的风险。当一个调查公司想要对 1000 个人进行调查，它们不是在电话亭里随机选 1000 个人出来。调查公司要保证这 1000 个人对人群整体有代表性。例如，美国人口的 51.3% 是女性，48.7% 是男性。所以在美国， 严谨的调查需要保证样本也是这个比例：513 名女性，487 名男性。这称作分层采样 （stratified sampling）：将人群分成均匀的子分组，称为分层，从每个分层去取合适数量的 实例，以保证测试集对总人数有代表性。如果调查公司采用纯随机采样，会有 12% 的概率导 致采样偏差：女性人数少于 49%，或多于 54%。不管发生那种情况，调查结果都会严重偏 差。假设专家告诉你，收入中位数是预测房价中位数非常重要的属性。你可能想要保证测试集可 以代表整体数据集中的多种收入分类。因为收入中位数是一个连续的数值属性，你首先需要 创建一个收入类别属性。

大多数的收入中位数的值聚集在 2-5（万美元），但是一些收入中位数会超过 6。数据集中的 每个分层都要有足够的实例位于你的数据中，这点很重要。否则，对分层重要性的评估就会 有偏差。这意味着，你不能有过多的分层，且每个分层都要足够大。后面的代码通过将收入 中位数除以 1.5（以限制收入分类的数量），创建了一个收入类别属性，用 ceil 对值舍入 （以产生离散的分类），然后将所有大于 5的分类归入到分类 5：
##income influence housing price ,so deal with income
housing[“income_cat”]=np.ceil(housing[“median_income”]/1.5)
housing[“income_cat”].where(housing[“income_cat”]<5,5,inplace=True)
#print housing[“income_cat”].head()

现在，就可以根据收入分类，进行分层采样。你可以使用 Scikit-Learn 的 StratifiedShuffleSplit 类：
split=StratifiedShuffleSplit(n_splits=1,test_size=0.2,random_state=42)
for train_index , test_index in split.split(housing,housing[“income_cat”]):
start_train_set = housing.loc[train_index]
start_test_set = housing.loc[test_index]
##income classify
print housing[‘income_cat’].value_counts()/len(housing)
print start_train_set.head()

地理数据可视化

因为存在地理信息（纬度和经度），创建一个所有街区的散点图来数据可视化是一个不错的 主意

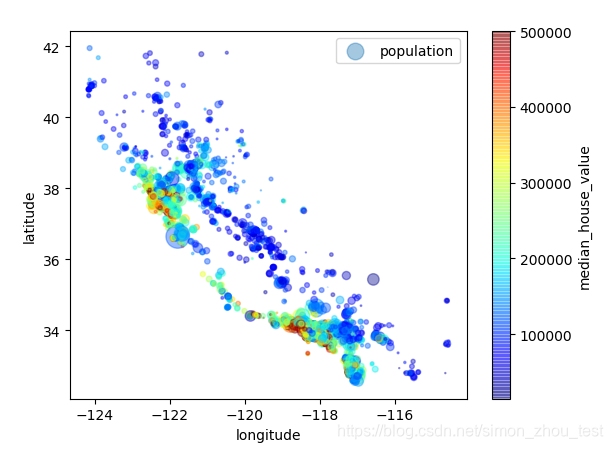
这张图说明房价和位置（比如，靠海）和人口密度联系密切，这点用聚类算法来检测主要的聚集，用一个新的特征值测量聚集中心的域的房价不是非常高，但离大海距离属性也可能很有用，所以这不以定义的问题。

查找关联

因为数据集并不是非常大，你可以很容易地使用 corr() 方法计算出数（standard correlation coefficient，也称作皮尔逊相关系数）：
恢复原始数据与新创建副本
###axis=1 row ,axis=0 column set use
for set in (start_train_set,start_test_set):
set.drop(“income_cat”,axis=1,inplace=True)

###ceate replication
housing=start_test_set.copy()
#housing.plot(kind=“scatter”,x=“longitude”,y=“latitude”,alpha=0.1)

相关系数的范围是 -1 到 1。当接近 1 时，意味强正相关；例如，当收入中位数增加时，房价 中位数也会增加。当相关系数接近 -1 时，意味强负相关；你可以看到，纬度和房价中位数有 轻微的负相关性（即，越往北，房价越可能降低）。最后，相关系数接近 0，意味没有线性相 关性。
attributes = [“median_house_value”, “median_income”, “total_rooms”, “housing_median_age”]

网上撤了一大堆没撤明白，2.7版本这样解决

pd.plotting.scatter_matrix(housing[attributes], figsize=(12, 8))

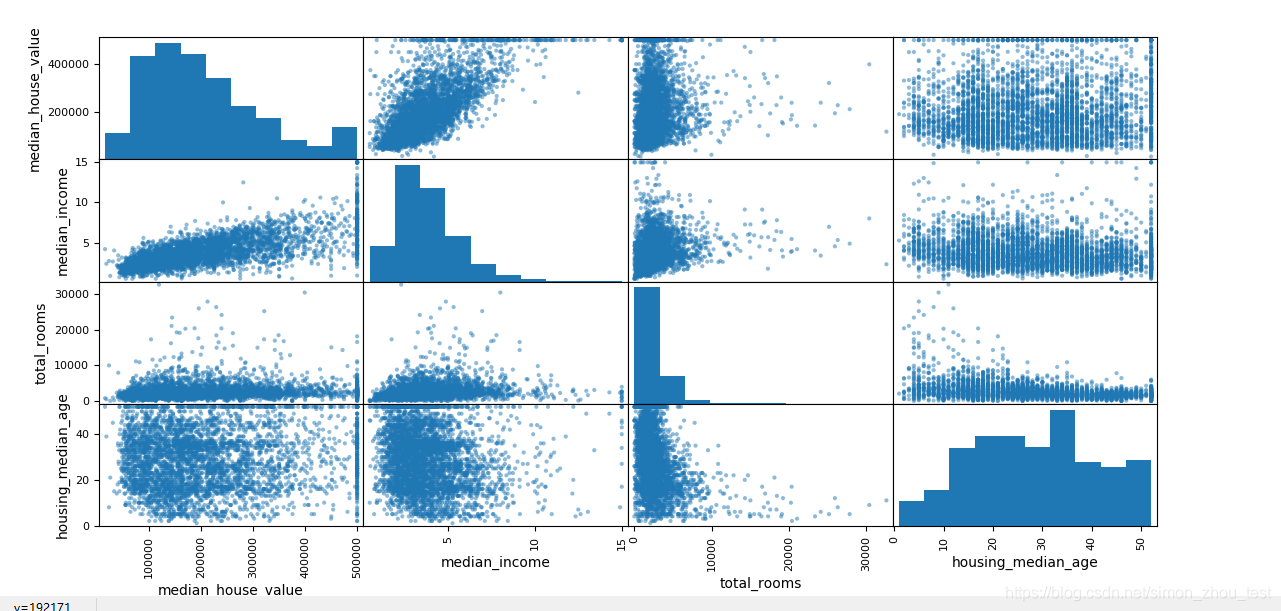
相关性最强的应该是收入属性。
###属性组合
housing[“rooms_per_household”] = housing[“total_rooms”]/housing[“households”]
housing[“bedrooms_per_room”] = housing[“total_bedrooms”]/housing[“total_rooms”]
housing[“population_per_household”]=housing[“population”]/housing[“households”]

scatter_matrix=housing.corr()
print scatter_matrix[‘median_house_value’].sort_values(ascending=False)
plt.show()

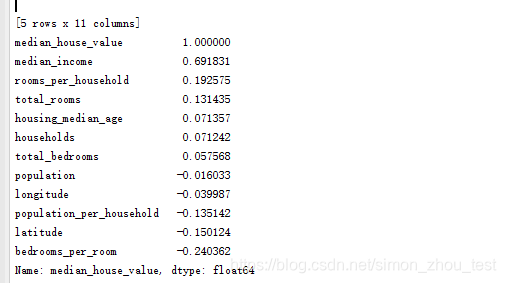
分析：与房价相关性最强的是收入，其次是每个屋子的卧室数，以及每个家庭的房间数，每个屋子的卧室数越大，房价越低。而每个房间数/家庭数越大，房价也越高。