排序算法：快速排序详解

学习快速排序之前首先要划分

划分方法：

每次选一个枢纽，根据枢纽进行划分：大于枢纽的放右边，小于枢纽的放左边

用left表示数组左端点，right表示右端点，pivot表示枢纽

void partition(int left, int right, int pivot){
        int lp=left-1;
        int rp=right+1;
        while(true){
            while(lp<right&&a[++lp]<pivot); //a为被排序的数组
            while(rp>left&&a[--rp]>pivot);
            if(lp>=rp) break;
            swap(lp,rp);
        }
}

划分的效率：比较N（+1，2）次，交换N/2次，最好情况下，比较N(+1,2)次，交换0次

这是因为，在退出循环之前，lp必然大于rp ，在退出之前就已经先比较过了大小，所以要比N要大

在进行快速排序时，不用人为定义一个枢纽，而是用数组的某个值来表示，一般采用数组最右端的值表示枢纽，此时代码：

int partition(int left, int right, int pivot){
        int lp=left-1;
        int rp=right;
        while(true){
            while(lp<right&&a[++lp]<pivot);
            while(rp>left&&a[--rp]>pivot);
            if(lp>=rp) break;
            swap(lp,rp);

        }
        swap(lp,right-1);
        return lp;
    }

注意代码的变化，

1.rp的值由right+1改为了right，这是因为pivot在最右端，不应该参与比较

2.当这次划分结束时，将pivot与lp位置的值进行调换，因为lp最后所指向的值必然大于pivot（退出while循环的条件），调换位置并不会影响结果（但会影响顺序，丧失稳定性），此时pivot已经处于它在最终排序所应该处于的位置了。

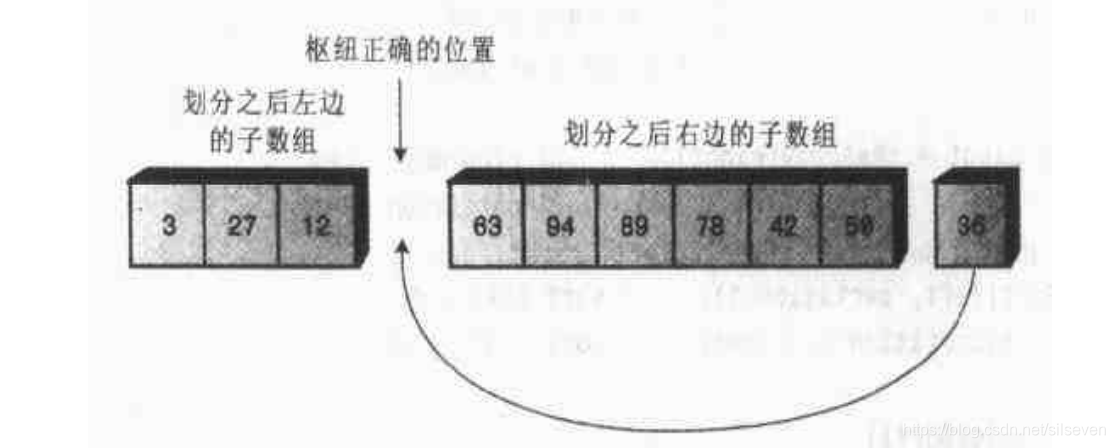
那么如何进行快速排序呢？

相信聪明的小伙伴已经发现了，只要对枢纽的两边一直划分下去，不就能得到有序数组了么

 void quickSort(int left, int right){
        if(right-left<=0) return;
        else{
            int pivot=a[right];
            int par = partition(left,right,pivot);
            quickSort(left,par-1);
            quickSort(par+1,right);
        }
    }

注意这里两个quicksort都不包含par本身，这是因为par已经有序了。

当要排序的数目小于等于1时也直接返回。

快速排序效率：

快排在最好情况下，每次都能选到中值，则总共需要进行log(N)次递归，每次递归都发生约N次比较，故时间效率为N*log(N)

最坏情况下，每次递归都是1和N-1，故需要N次递归，效率为N^2/2，与冒泡排序相同。

那么如何避免最坏情况呢（即逆序）？

采取三数据取中的划分方法，不再取最右端数据为枢纽，而是从左端，中间，右端三个值中选出一个中间值用以充当枢纽。

并且消除了rp>left和lp<right的判定条件，因为三数据项排序以后，左端数据一定比枢纽小，那么原来的判定条件a[--rp]>pivot 在最左端时一定为false，故会跳出循环。右端同理。

但注意，当length<=2时，不能使用三数据取中方法，因为lp总会先+1，而mid会向下取整，即原来lp的位置，而每次partition都会交换lp和mid的数值如果本身有序，则会导致乱序。

int partition(int left, int right, int pivot){
        int lp=left;
        int rp=right-1;
        while(true){
            while(lp<right&&a[++lp]<pivot);
            while(rp>left&&a[--rp]>pivot);
            if(lp>=rp) break;
            swap(lp,rp);

        }
        swap(lp,right-1);
        return lp;
    }

    int median(int left, int right){
        int mid = (left+right)/2;
        if(a[left]>a[mid]) swap(left,mid);
        if(a[left]>a[right]) swap(left,right);
        if(a[mid]>a[right]) swap(mid,right);

        swap(mid,right-1);
        return a[right-1];

    }

    void quickSort(int left, int right){
        if(right-left<=0) return;
        if(right-left==1){
            if(a[left]>a[right]) swap(left,right);
        }
        else{
            int mid = median(left,right);
            int par = partition(left,right,mid);
            quickSort(left,par-1);
            quickSort(par+1,right);
        }
    }

(如需转载，请标明出处）

参考资料：

《Java数据结构与算法 第二版》 Robert Lafore