1.二叉树搜索树
1.1 数据结构
binary search tree是有序二叉树搜索树。
- 每个节点只存储一个关键字
- 非叶子结点存在两个指针,其关键字大于左子节点关键字,小于右子节点关键字
其特点是不平衡,树形结构的收到插入和删除节点的顺序影响,随机性很大。B树的深度为d log(n)<d< n,其搜索的时间复杂度是O(d),即最大是O(n),最小是O(log(n)),取决于树的形态。 通常实际应用中选用优化版本,平衡二叉树(即每个叶子结点高度相差小于1),平衡二叉树的搜索性能接近二分查找。
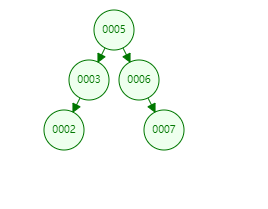
例如数字1-10按照 5、8、9、3、4、2、7、1、10、6顺序构建,结构如下:
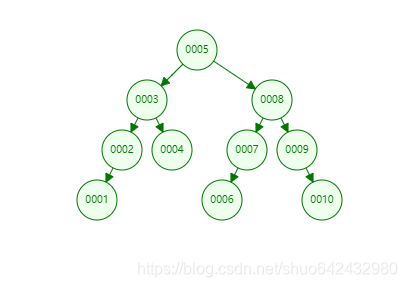
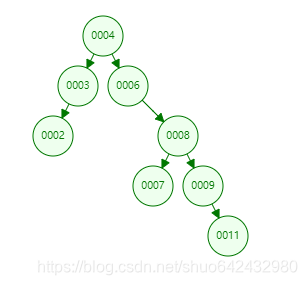
当插入顺序是:1,2,3,4,5,6,7,8,9,10 时,此时其查询效率变成了线性搜索,其结构如下:

1.2 增删改查操作:
1.2.1查询
- 从根节点开始搜索;
- 如果目标关键字等于当前节点关键字,返回结果;
- 如果目标关键字小于当前节点关键字去左子树继续查找;
- 如果目标关键字大于当前节点关键字,去右子树查找;
- 当前节点关键字左右指针为空,返回无此关键字。
1.2.2插入
- 如果树是空树,插入节点作为根节点;

- 若子树指针为空,将子树指针指向目标节点,插入完毕。
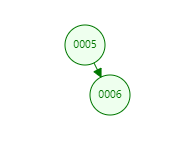
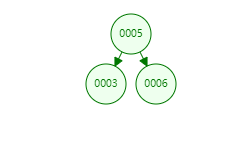
- 如果目标关键字小于当前节点关键字,搜索其左子树;
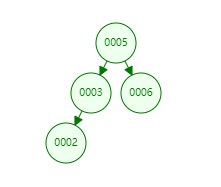
- 如果目标关键字大于或等于当前节点关键字,搜索其右子树;
1.2.3删除
- 如果目标节点没有孩子节点,直接删除节点,将其父节点指针设置成空;
例如下图删除1节点
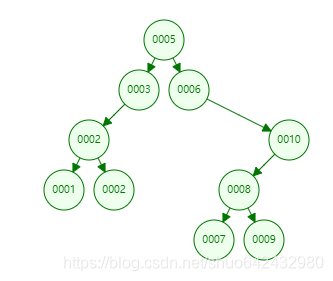
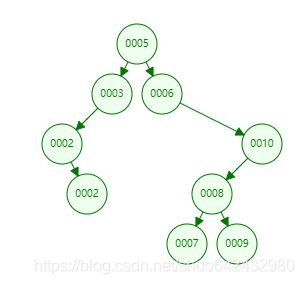
- 如果目标节点只有左孩子,将其父节点指向目标节点的指针指向孩子节点,删除目标节点;
例如下图删除10节点:
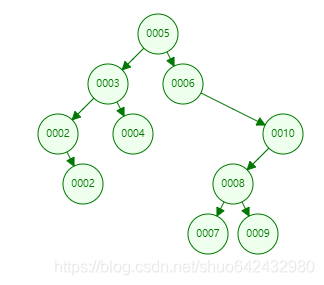
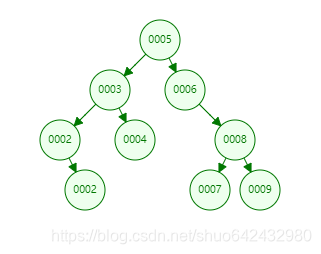
- 如果目标节点只有右孩子,将其父节点指向目标节点的指针指向孩子节点,删除目标节点;
例如下图删除10节点
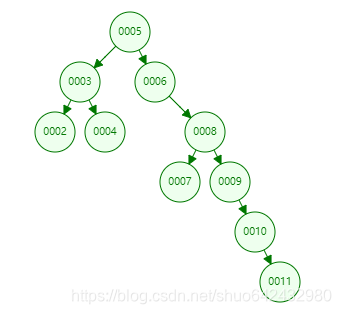
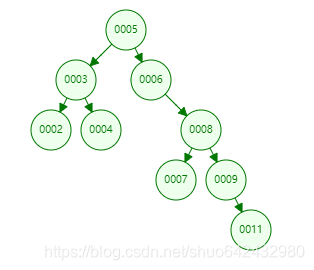
- 如果目标节点有两个孩子,为了保证树的平衡,需要挑选替代节点,可以挑选左子树最右节点,也可以挑选右子树最左节点。
例如下图删除5节点,选取左子树最右节点4作为替代节点:
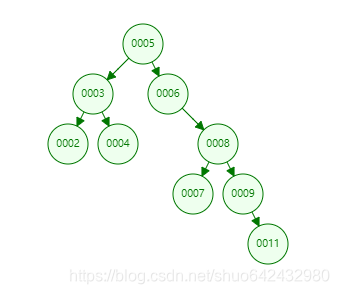





















 2094
2094

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








