分析算法

分析算法

• 在分析算法的过程中，通常我们想度量的是计算时间。
• 我们算法的分析，都假定一种通用的单处理器计算模型——随机访问机（random-access machine, RAM），没有并发操作。
• RAM 模型包含真实计算机中常见的指令：算术指令、数据移动指令和控制指令。每条这样的指令所需时间都为常量。

过程 INSERTION-SORT 需要的时间依赖于输入，不仅指的是输入的数目，也依赖于它们已被排序的程度。

一个算法在特定输入上的运行时间是指执行的基本操作数或步数。

我们假定：执行每行伪代码需要常量时间，即第 i 行的每次执行需要时间常量 Ci;

for j = 2 to A.length                                   c1      n
    key = A[j]                                          c2      n-1
    // Insert A[j] into the sorted sequence A[1..j-1].  0       n-1 
    i = j-1                                             c4      n-1
    while i > 0 and A[i] > key                          c5      sum(t_j, j=2, n)
        A[i+1] = A[i]                                   c6      sum(t_j-1, j=2, n)
        i = i -1                                        c7      sum(t_j-1, j=2, n)
    A[i+1] = key                                        c8      n-1

所有运行的时间：

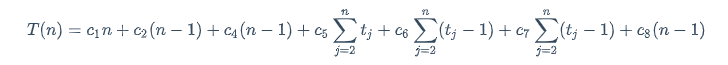
最佳的运行情况：

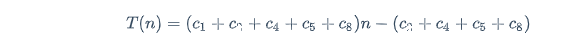
我们可以将该运行时间表示为 an+b；它是 n的线性函数。
最坏情况：

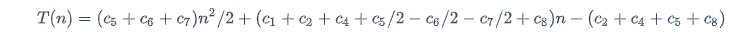
它是n的二次函数；

最坏情况和平均情况分析

往往我们集中于只求最坏情况运行时间，理由有三：

• 可以给出一个上界；
• 最坏情况经常出现；
• “平均情况”往往与最坏情况一致一样差。

增长量级

我们真正感兴趣的是运行时间的增长率或增长量级。
如果一个算法的最坏情况运行时间具有比另一个算法更低的增长量级，那么我们通常认为前者比后者更有效。