spark程序中cache的作用 + 实验

spark中cache的作用:

图例:

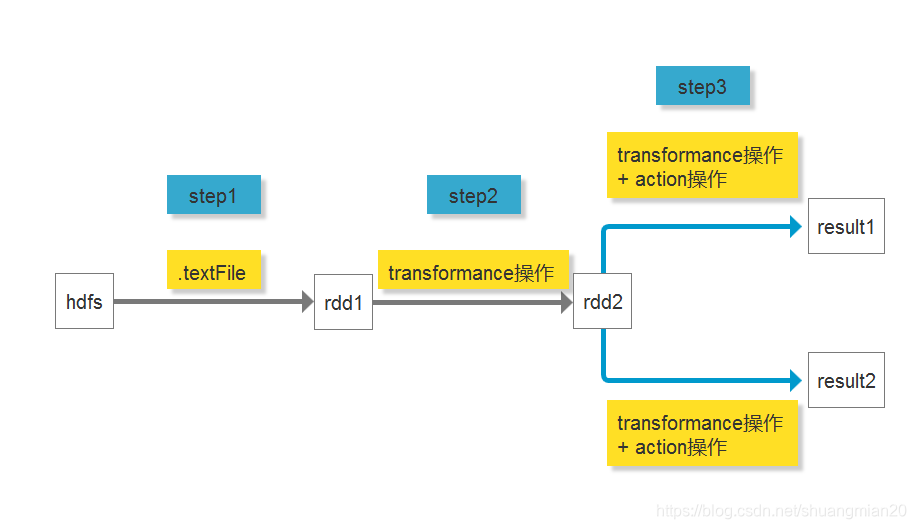
其中, result1和result2用到了同一个rdd(rdd2)做操作

如果rdd2不加cache:

由于spark程序为lazy操作, 所以在计算result1时, step1 -> step2 -> step3会全部走一遍, 计算result2时, step1 -> step2 -> step3也会全部走一遍, 其中step1 -> step2为重复步骤, 浪费了资源

如果rdd2加了cache:

计算result1时, step1 -> step2 -> step3会全部走一遍, 计算result2时, 直接从cache中取出rdd2, 只走了step3

实验:

demo代码1(rdd2不加cache):

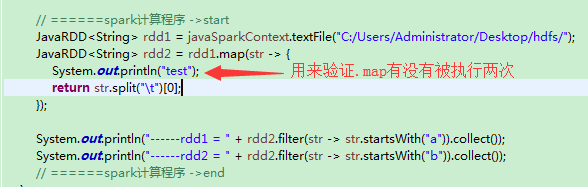
其中rdd2没有加cache, 目录:C:/Users/Administrator/Desktop/hdfs/只加了两条日志, 所以结果应该是控制台输出了两组"test"(每组两个"test")

实验结果:

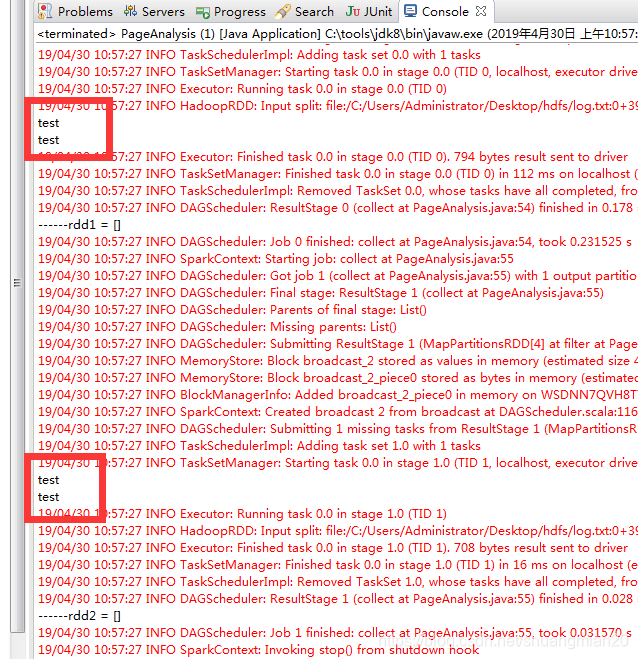
demo代码1(rdd2添加cache):

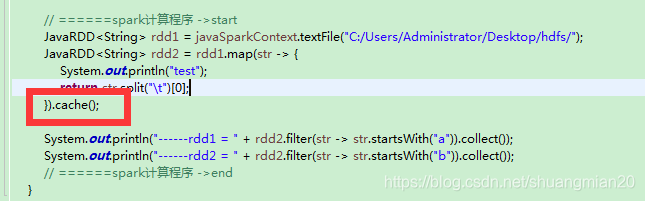
其中rdd2被cache, 所以结果应该是只输出了一组"test"(一组两个"test").

实验结果:

结论:

如果两个以上的计算步骤要使用同一个rdd, 建议使用cache

关键字:

spark离线计算, cache

个人说明:
阿幕, 一个喜欢听电音/trap/rnb, 喜欢看动漫, 喜欢玩我的世界的程序员