机器学习【ROC曲线&AUC&KS】

一、基础概念

• TP（真正例）：实际为正类且预测为正类的样本数；
• FP（假正例）：实际为负类但预测为正类的样本数；
• TN（真负例）：实际为负类且预测为负类的样本数；
• FN（假负例）：实际为正类但预测为负类的样本数。

通俗解释：T,F代表预测是否正确；P,F指的是预测值；

如何理解记忆：正（T）正(P)实际为真，否(F)否(N)实际为真，一正(T|F)一负(N|P)实际为假

• 真正例率（TPR）：正类样本中被正确预测的比例（“敏感性”“召回率”）：TPR=TP/(TP+FN)（分子是正确识别的正类，分母是所有实际正类；相当于在一个标签全为1的数据集中，模型正确预测为1的概率——把真的当作真的概率。TPR 越高，模型识别正类的能力越强）

• 假正例率（FPR）：负类样本中被错误预测为正类的比例：FPR=FP/(FP+TN)（分子是错误识别的负类，分母是所有实际负类，相当于在一个标签全为0的数据集中，模型错误预测为1的概率——把假的当作真的概率。FPR 越高，模型误判负类的概率越大）

二、ROC曲线

2.1、ROC 曲线的核心价值是评估模型在 “不同阈值下的综合表现” 和 “对正负类的排序能力”

        通过设定不同的阈值来预测结果，获得不同的TPR，FPR的坐标点集。以FPR作为横轴，TPR为纵轴，将点集拟合成ROC曲线

2.2、举例：

        假设我们有 5 个样本：

• 真实标签 y_true = [1, 1, 0, 0, 0]（2 个正类，3 个负类）；
• 预测概率 y_score = [0.8, 0.6, 0.5, 0.3, 0.2]。

        a.遍历阈值计算 FPR 和 TPR：

• 阈值 = 0.9：所有样本预测为负类（y_score < 0.9）→ TP=0，FP=0 → TPR=0/(0+2)=0，FPR=0/(0+3)=0 → 点 (0,0)；
• 阈值 = 0.7：y_score ≥0.7 的样本是第 1 个（0.8）→ 预测正类 1 个 → TP=1（第 1 个是正类），FP=0 → TPR=1/2=0.5，FPR=0/3=0 → 点 (0, 0.5)；
• 阈值 = 0.5：y_score ≥0.5 的样本是第 1、2、3 个（0.8,0.6,0.5）→ 预测正类 3 个 → TP=2（前 2 个是正类），FP=1（第 3 个是负类）→ TPR=2/2=1，FPR=1/3≈0.33 → 点 (0.33, 1)；
• 阈值 = 0.2：所有样本预测为正类 → TP=2，FP=3 → TPR=1，FPR=3/3=1 → 点 (1,1)。

        b.得到的 ROC 曲线

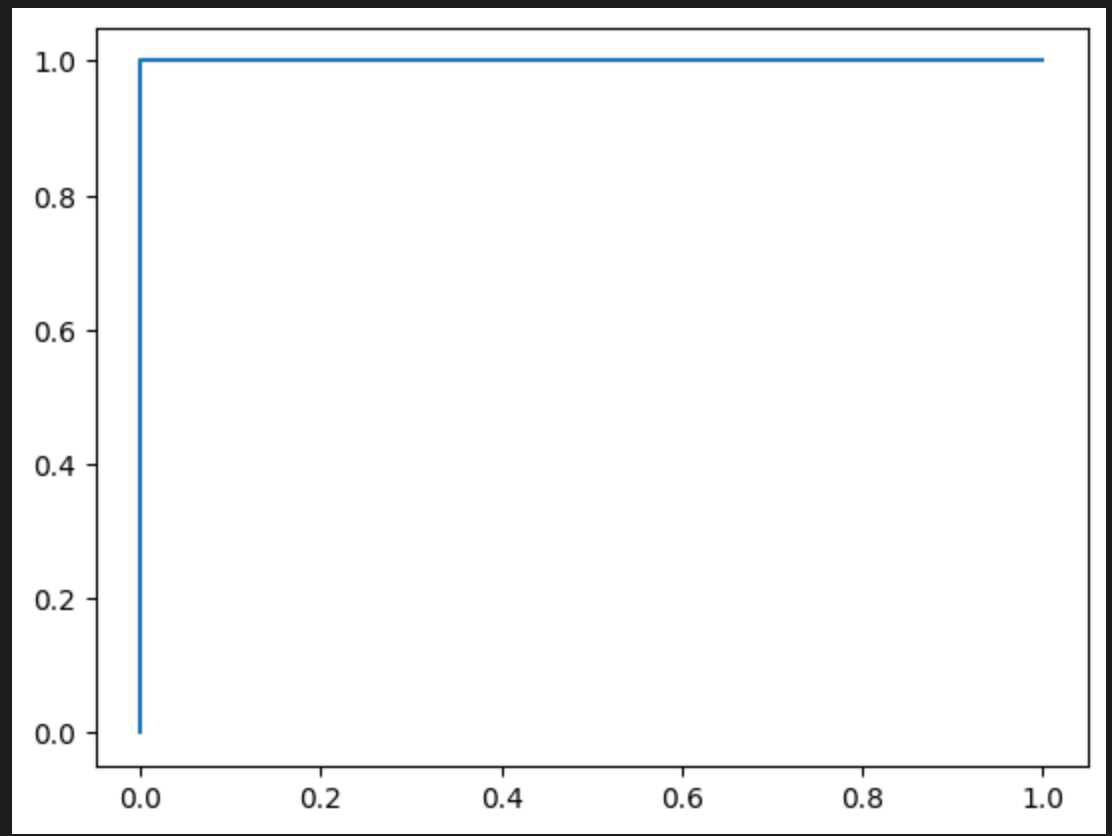
        将上述点 [(0,0), (0,0.5), (0.33,1), (1,1)] 连接，就是该模型的 ROC 曲线。曲线越靠近左上角，说明模型排序能力越强（本例中，正类的预测概率 [0.8,0.6] 整体高于负类 [0.5,0.3,0.2]，因此曲线较好）。

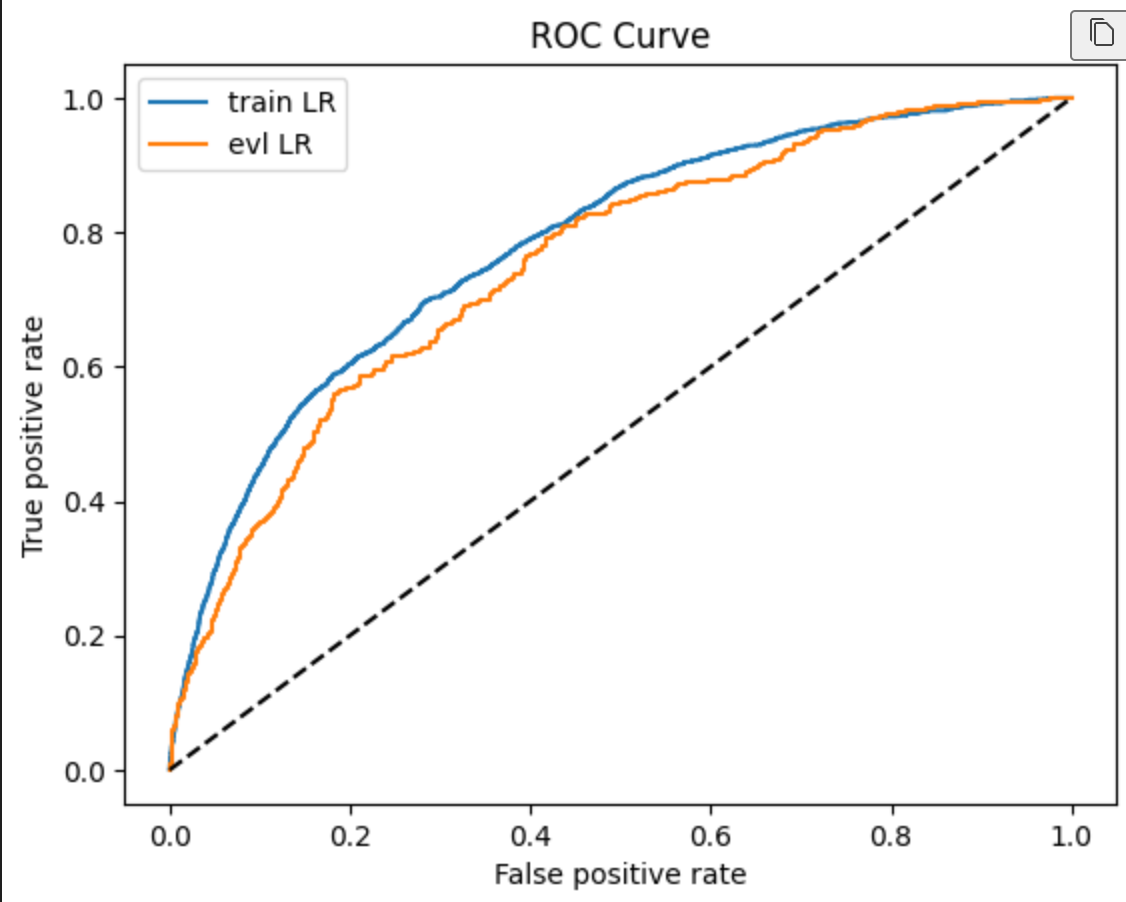
三、AUC

3.1、基础概念

        AUC（Area Under ROC Curve，ROC 曲线下面积）是二分类模型评估中最核心、最通用的指标之一，其核心意义可以概括为：衡量模型对 “正类” 和 “负类” 的 “整体排序能力”—— 即模型能否把 “实际为正类的样本” 排在 “实际为负类的样本” 前面。

        AUC 的本质是一个概率值，可以用一句话解释：随机从数据中选一个正类样本和一个负类样本，模型对正类样本的预测概率大于负类样本的概率，这个事件发生的概率就是 AUC 值。

例如：

• 若 AUC=0.8，说明在 80% 的情况下，随机选一个正样本（如 “违约用户”）和一个负样本（如 “正常用户”），模型给正样本的 “违约概率” 会高于负样本；
• 若 AUC=0.5，说明模型对正负样本的排序和 “抛硬币” 一样（随机猜测），毫无区分能力；
• 若 AUC=1，说明模型能 100% 正确排序：所有正样本的预测概率都高于负样本（完美模型）。

3.2、核心意义

a. 评估模型的 “整体区分能力”，不受分类阈值影响

        二分类模型的预测结果依赖 “分类阈值”（如 “预测概率 > 0.5 则判为正类”），但不同场景的阈值选择不同（如风控中可能用 0.3，医疗中可能用 0.7）。

        AUC 的价值在于：它不依赖具体阈值，而是综合衡量模型在 “所有可能阈值下” 的表现。无论阈值如何调整，AUC 都能反映模型对正负样本的 “内在排序能力”—— 只要正样本的预测概率整体高于负样本，AUC 就会接近 1。

b. 对 “类别不平衡” 数据更稳健

        在实际业务中，数据往往是不平衡的（如 “违约用户” 仅占 1%，“正常用户” 占 99%）。此时，传统指标（如 “准确率”）会失效（例如：模型全预测 “正常”，准确率也能达到 99%，但毫无意义）。而 AUC 基于TPR（正类识别率）和 FPR（负类误判率） 计算（两者分别基于 “实际正类总数” 和 “实际负类总数”），不受样本比例影响。即使正类仅占 1%，AUC 仍能客观反映模型是否能把这 1% 的正类和 99% 的负类区分开。

四、KS（Kolmogorov-Smirnov)

KS 的本质：“最大区分度” 的量化

        KS 的计算逻辑是 “FPR（假正例率）与 TPR（真正例率）的最大差值的绝对值”（即 KS = max(|TPR - FPR|)）。

KS 值的大小直观体现了模型能在多大程度上把正类和负类分开：

• 若 KS=0.4，说明存在一个阈值，在该阈值下，模型正确识别的正类比例（TPR）比错误识别的负类比例（FPR）高出 40%（例如 TPR=60%，FPR=20%，差值 40%）；
• 若 KS=0.1，说明即使在最佳阈值下，模型对正负类的区分也很弱（比如 TPR=55%，FPR=45%，仅差 10%）。

简言之：KS 值越大，模型在某个阈值下的 “正类识别” 与 “负类保护” 的平衡效果越好。