(整理)关于二叉树的基础知识

任何一个可以用计算机求解的问题所需的计算时间都与其规模有关.问题的规模越小,解题所需的计算时间往往越少,从而也较容易处理.

分治法设计思想:将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之 递归算法就是由分治法设计思想产生的.

一个直接或间接地调用自身的算法称为递归算法.一个使用函数自身给出定义的函数称为递归函数

迭代是循环结构,递归是选择结构

二叉树(Binary Tree)是n(n>=0)个节点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的,分别称为根结点的左子树和右子树的二叉树组成. 根节点没有双亲 叶节点没有孩子

特点:

每个结点最多有两棵子树(左子树和右子树,不能大于两棵,只有一棵或者是空树都可以)

左子树和右子树是有顺序的

即使树中某结点只有一棵子树,也要区分它是左子树还是右子树(手型对称特点,访问左不等于访问右)

特殊二叉树:

1. 斜树:只有左子树的二叉树(左斜树),只有右子树的二叉树(右斜树),结点的个数与二叉树的深度相同

2. 满二叉树:如果所有的分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树被称为满二叉树, 满二叉树是特殊的完全二叉树

局部是满二叉树,全局不一定满二叉树, 同理可得完全二叉树

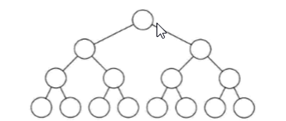
特点:

叶子只能出现在最下一层,出现在其它层就不可能达成平衡.

 非叶子节点的度(结点拥有的子树数)一定是2

 在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多

3 完全二叉树

对于深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树(编号连续)

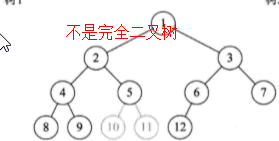
满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树

特点:

  叶子结点只能出现在最下两层;

  最下层的叶子一定集中在左边连续位置

 倒是第二层若有叶子结点,一定都在右边连续位置

如果结点度为1,该结点只有左孩子,不存在只有右子树的情况;

 同样结点数的二叉树,完全二叉树的深度最小

二叉树性质:
1.
2.
3.
对任何一棵二叉树,如果其终端结点数(叶子结点数)为n0,度为2的结点数为n2,则n0=n2+1
4.

二叉树的遍历

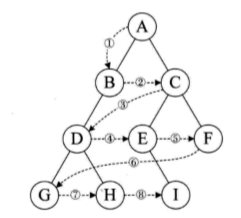
1. 前序遍历

若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树

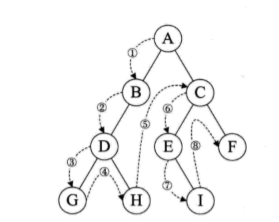
2. 中序遍历

若树为空,则空操作返回,否则从根结点开始,中序遍历根结点的左子树,然后访问根结点,最后遍历右子树

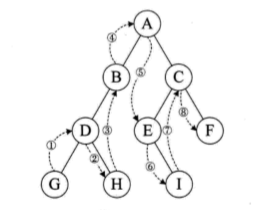
3. 后序遍历

若树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后访问根结点.

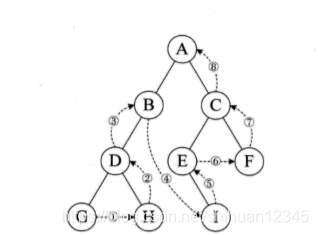
4.层次遍历

若树为空,则空操作返回,否则从树的第一层,也就是 根结点开始访问,从上到下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问.