用Go实现一个状态机_状态流转go-优快云博客

工作中，很多同学会用到状态机，例如对一个工单进行创建、编辑、审核，在执行新动作前，要检查能否从当前状态流转到下一个状态。对这种需求，我们怎么实现呢？

数组

在Go设计模式(22)-状态模式中说过，简单的状态管理使用数组即可完成，无需使用状态模式。以下图为例，状态之间的流转，无法跳跃，即只能从编辑中跳到提交，无法直接从编辑中跳到审核通过。

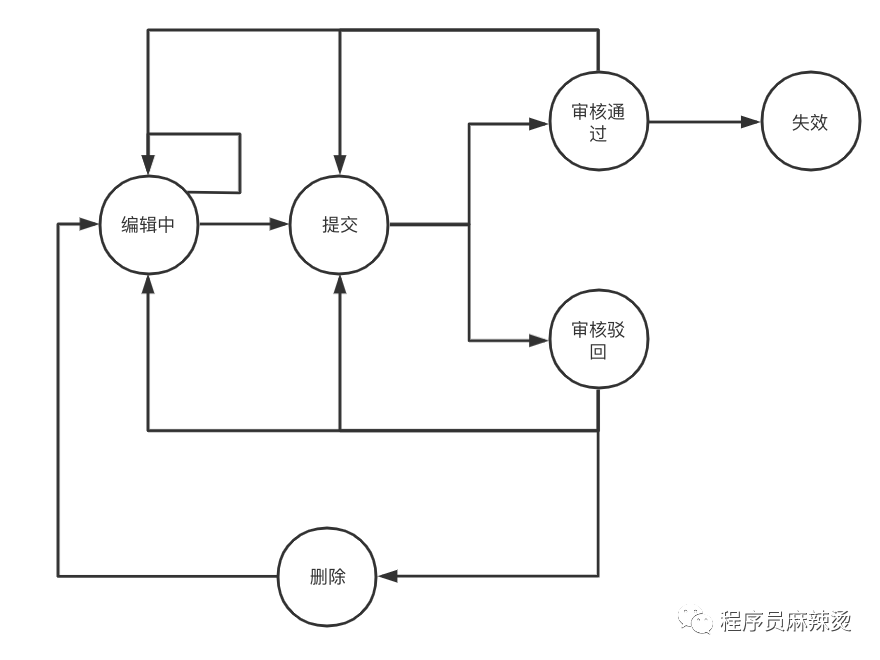
这种实现方案很简单，配置数组用于检查：

func (s *shopWarehouse) statusCheck(currentStatus, targetStatus int64) bool {
	//target -> currents
	statusMap := map[int64][]int64{
		consts.Editing: []int64{consts.Editing, consts.Pass, consts.Reject},
		consts.Submit:  []int64{consts.Editing, consts.Reject},
		consts.Pass:    []int64{consts.Submit},
		consts.Reject:  []int64{consts.Submit},
		consts.Invalid: []int64{consts.Pass},
		consts.Delete:  []int64{consts.Reject, consts.Editing},
	}
	if statusList, ok := statusMap[targetStatus]; ok {
		if util.InArray(currentStatus, statusList) {
			return true
		}
		return false
	} else {
		return false
	}
}

数组在设置上，可以设置为target->current，也可设置为为current->target，current->target更易于理解。

状态检查需要两步，先查询当前状态，然后调用statusCheck函数，但两个操作之间，若有其它线程更改了当前状态呢？

其实可以用Go中加锁的例子进行解释，在Go锁，我终于搞懂了中，加互斥锁也分两步，获取当前状态，然后执行CAS，必然会遇到并发情况，对当前状态进行了变更。但没有影响，因为只要更新的那一刻，我们关注的数据状态没有变化，那就说明变更合法的，直接更新即可。

将状态放到数组里统一维护，比将各个状态分散开判断，在设计上要好得多。

图

上面的流转比较简单，而且没有跳跃情况。如果状态十分多，而且会跳跃，再用数组方案，维护成本极高。

此时，图的作用就发挥出来了。分支限界法和回溯法里有很多广度优先遍历和深度优先遍历的例子，希望可以帮助大家回忆起相关算法。

这里先举一个状态流转例子：

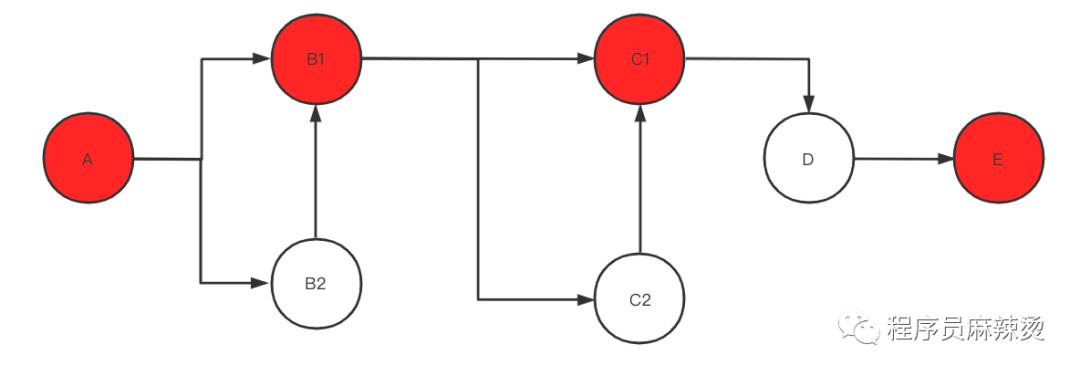
其中红色表示必须经过的节点，白色可以跳过，对于这种情况，我们应该怎样实现呢？

package main

import (
   "fmt"
   "reflect"
)

// 时序图
var StatusTimingGraph = map[string][]string{
   "A":  {"B1", "B2"},
   "B1": {"C1", "C2"},
   "B2": {"B1"},
   "C1": {"D"},
   "C2": {"C1"},
   "D":  {"E"},
}

// 核心节点
var CoreStatus = []string{
   "A",
   "B1",
   "C1",
   "E",
}
var StatusJumpGraph = InitJumpGraph(StatusTimingGraph, CoreStatus)

func InitJumpGraph(statusMap map[string][]string, coreStatus []string) map[string][]string {
   retMap := make(map[string][]string, 0)
   for status, statusList := range statusMap {
      retList := make([]string, 0)
      for _, tStatus := range statusList {
         retList = append(retList, tStatus)
         if InSlice(coreStatus, tStatus) {
            continue
         }
         tList := recursionGraph(tStatus, statusMap, coreStatus)
         for _, tStatus := range tList {
            if !InSlice(retList, tStatus) {
               retList = append(retList, tStatus)
            }
         }
      }

      retMap[status] = retList
   }
   return retMap
}
func recursionGraph(status string, statusMap map[string][]string, coreStatus []string) []string {
   retList := make([]string, 0)
   if statusList, ok := statusMap[status]; ok {
      for _, tStatus := range statusList {
         retList = append(retList, tStatus)
         if InSlice(coreStatus, tStatus) {
            continue
         }
         retList = append(retList, recursionGraph(tStatus, statusMap, coreStatus)...)
      }
   }
   return retList
}
func InSlice(a, b interface{}) bool {
   exist, _ := InSliceWithError(a, b)
   return exist
}
func InSliceWithError(a, b interface{}) (exist bool, err error) {

   va := reflect.ValueOf(a)

   if va.Kind() != reflect.Slice {
      err = fmt.Errorf("parameter a must be a slice")
      return
   }

   if reflect.TypeOf(a).String()[2:] != reflect.TypeOf(b).String() {
      err = fmt.Errorf("type of parameter b not match with parameter a")
      return
   }

   for i := 0; i < va.Len(); i++ {
      if va.Index(i).Interface() == b {
         exist = true
         return
      }
   }

   return
}

func main() {
   originStatus := "A"
   targetStatus := "B1"
   statusList, ok := StatusJumpGraph[originStatus]
   fmt.Println(StatusJumpGraph)
   if !ok {
      fmt.Println("状态有误")
      return
   }

   if !InSlice(statusList, targetStatus) {
      fmt.Println("状态不合规，无法流转")
      return
   }
}