[Java]堆排序代码实现

最新推荐文章于 2023-01-04 11:09:21 发布

ShichimiyaSatone

最新推荐文章于 2023-01-04 11:09:21 发布

阅读量263

点赞数

CC 4.0 BY-SA版权

分类专栏： Java 文章标签：堆排序算法 Java 代码实现

本文链接：https://blog.youkuaiyun.com/shichimiyasatone/article/details/90139986

Java 专栏收录该内容

21 篇文章

订阅专栏

本文深入解析了堆排序算法，详细介绍了堆的概念、堆排序的基本思想及步骤，并通过代码实现展示了如何将数组调整为大顶堆，最终完成排序过程。通过实例演示，读者可以直观理解堆排序的工作原理。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、堆介绍

堆为特殊完全二叉树，满足以下条件为完全二叉树：

1）从作为第一层的根开始，除了最后一层之外，第n层的元素个数都必须是 $2^{n-1}$ ；

2）叶子节点从左向右排放。

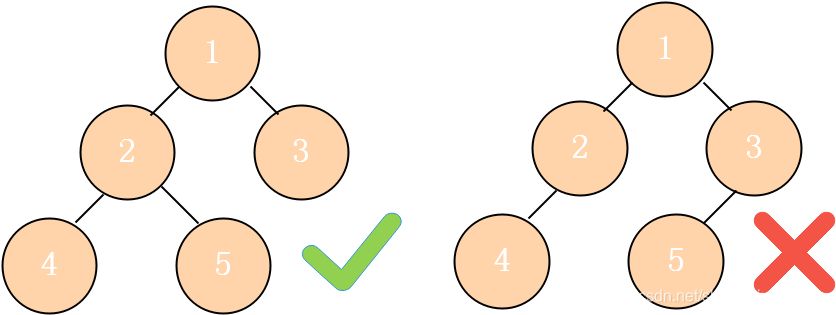
本次排序用到的堆为大顶堆，特点为所有父节点比其子节点大。

二、堆排序思想

排序中将用数组模拟堆，不会用到堆的链表结构。以下执行步骤：

1）将数组视为无序堆，下标对应的结点顺序可以参照上方完全二叉树示例图；

2）从第一个无叶子的结点开始，进行自下而上的堆调整，将当前结点形成的子堆堆调整为大顶堆，从而使得整个堆变成大顶堆；

2.1）该节点的计算方法， $array.length\div 2-1$ ；

2.2）调整方法，父节点与子节点选出最大结点与父节点置换。子节点下标， $i\ast 2+1,i\ast 2+2$ (可能不存在)；

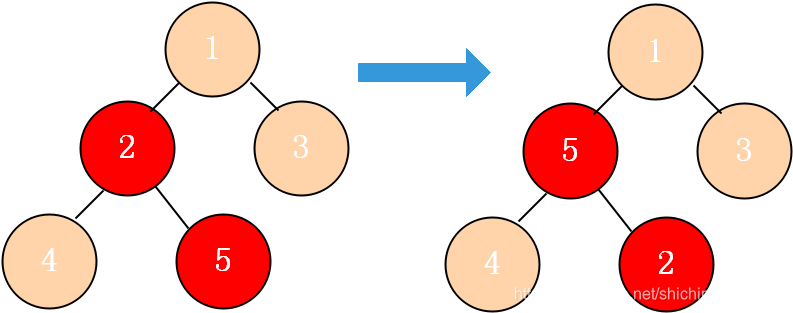
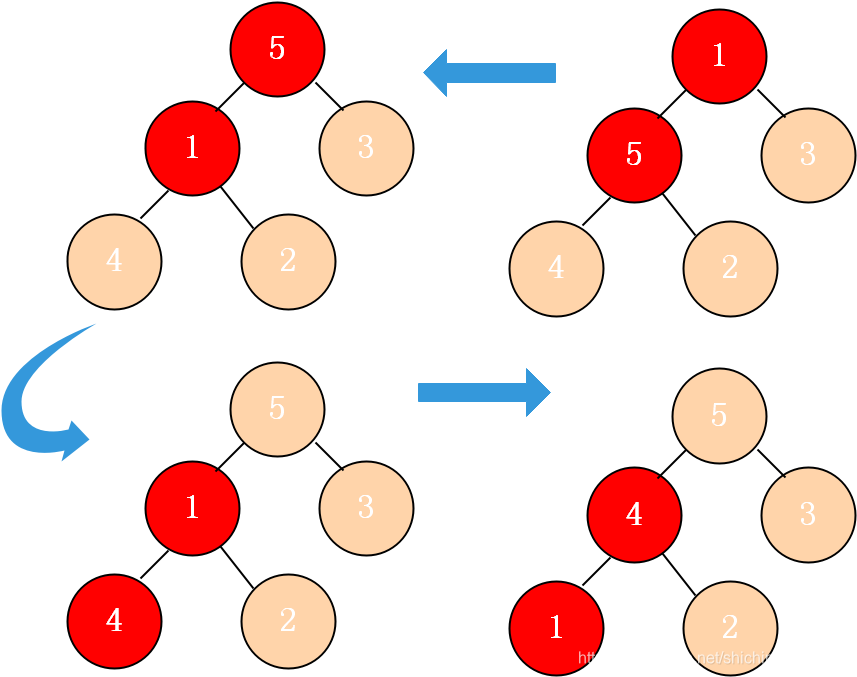
3）此时堆顶为最大值，与堆尾置换；

4）置换导致子堆（最大堆）结构被破坏，堆大小减1（堆尾最大值不参与调整），调整以根结点形成的子堆；

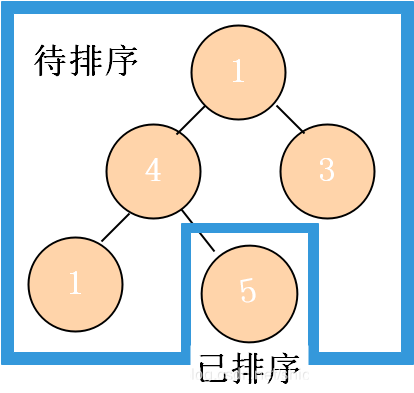
5）重复3、4步骤，直至目标堆大小为0。

三、代码实现

public class TestSort {
    @Test
    public void testSort(){
        int[] array = new int[11];
        for (int i = 0; i < array.length; i++) {
            array[i] = new Random().nextInt(100);
        }
        System.out.println("Before:"+Arrays.toString(array));
        heapSort(array);
        System.out.println("After:"+Arrays.toString(array));
    }
  
    // 堆排序
    private void heapSort(int[] array) {
        // 自上而上，调整所有节点的子树为大顶堆
        for (int i = array.length/2-1; i >=0 ; i--) {
            // 待调整的堆数组，调整的位置，需要调整的堆数组长度
            // 使i为父结点的子树形成大顶树
            AdjustHeap(array,i,array.length);
        }
        for (int i = array.length-1; i > 0; i--) {
            // 将堆顶置于最后
            swap(array,0,i);
            // 置换使得以0为父节点的大顶堆混乱，调整0位
            AdjustHeap(array,0,i);
        }
    }

    // 调整堆为大顶堆
    private void AdjustHeap(int[] array, int i ,int length) {
        for (int j = i*2+1; j <length ; j = j*2+1) {
            if (j+1<length && array[j+1]>array[j]){
                j++;
            }
            if (array[j]>array[i]){
                swap(array,i,j);
                i = j;
            }else {
                // 因为初始堆是自下而上调整的，子树已经为大顶堆
                // 当前根结点已经是最大值（无置换），直接退出循环
                break;
            }
        }
    }
}

四、测试结果

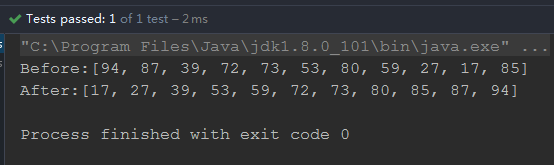
参考：堆排序详解 - 前程明亮