第三节 堆及其应用

于 2019-01-24 16:54:16 发布
阅读量392 收藏 1
点赞数 1
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/shenyixuanruoruo/article/details/86629360

第三节 堆及其应用

一、预备知识

完全二叉树：

    如果一棵深度为K二叉树，1至k-1层的结点都是满的，即满足2i-1，只有最下面的一层的结点数小于2i-1，并且最下面一层的结点都集中在该层最左边的若干位置，则此二叉树称为完全二叉树。

二、堆的定义

    堆结构是一种数组对象，它可以被视为一棵完全二叉树。树中每个结点与数组中存放该结点中值的那个元素相对应，如下图：

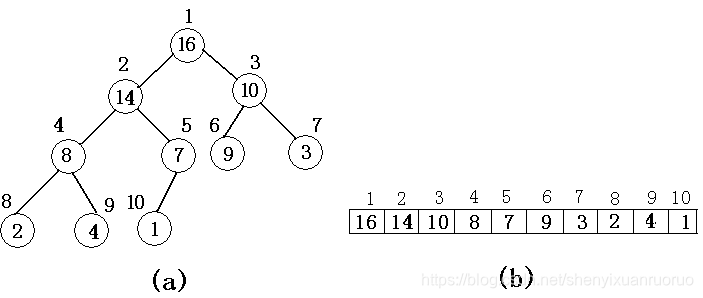
三、堆的性质

    设数组A的长度为len，二叉树的结点个数为size，size≤len，则A[i]存储二叉树中编号为i的结点值（1≤i≤size），而A[size]以后的元素并不属于相应的堆，树的根为A[1]，并且利用完全二叉树的性质，我们很容易求第i个结点的父结点（parent(i)）、左孩子结点(left(i))、右孩子结点(right(i))的下标了,分别为：i/2、2i、2i+1；
    更重要的是，堆具有这样一个性质，对除根以外的每个结点i，A[parent(i)]≥A[i]。即除根结点以外，所有结点的值都不得超过其父结点的值，这样就推出，堆中的最大元素存放在根结点中，且每一结点的子树中的结点值都小于等于该结点的值，这种堆又称为“大根堆”；反之，对除根以外的每个结点i，A[parent(i)]≤A[i]的堆，称为“小根堆”。

四、堆的操作

    用堆的关键部分是两个操作：put操作，即往堆中加入一个元素；get操作，即从堆中取出并删除一个元素。

1、往堆中加入一个元素的算法(put)如下：

　　（1）在堆尾加入一个元素，并把这个结点置为当前结点。
　　（2）比较当前结点和它父结点的大小
                  如果当前结点小于父结点，则交换它们的值，并把父结点置为当
                  前结点。转（2）。
                  如果当前结点大于等于父结点，则转（3）。
        （3）结束。

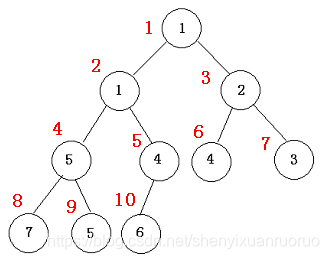
    重复n次put操作，即可建立一个小根堆。我们举一个例子看看具体过程：设n=10，10堆的数量分别为：3 5 1 7 6 4 2 5 4 1。
    设一个堆结构heap[11],现在先考虑用put操作建一个小根堆，具体方法是每次读入一个数插入到堆尾，再通过调整使得满足堆的性质(从堆尾son=len开始，判断它与父结点son/2的大小，若heap[son]<heap[son/2]，则交换这两个数，且son=son/2，继续判断heap[son]与heap[son/2]的大小，……直到son=1或者heap[son]>=heap[son/2]为止)。开始时堆的长度len=0。

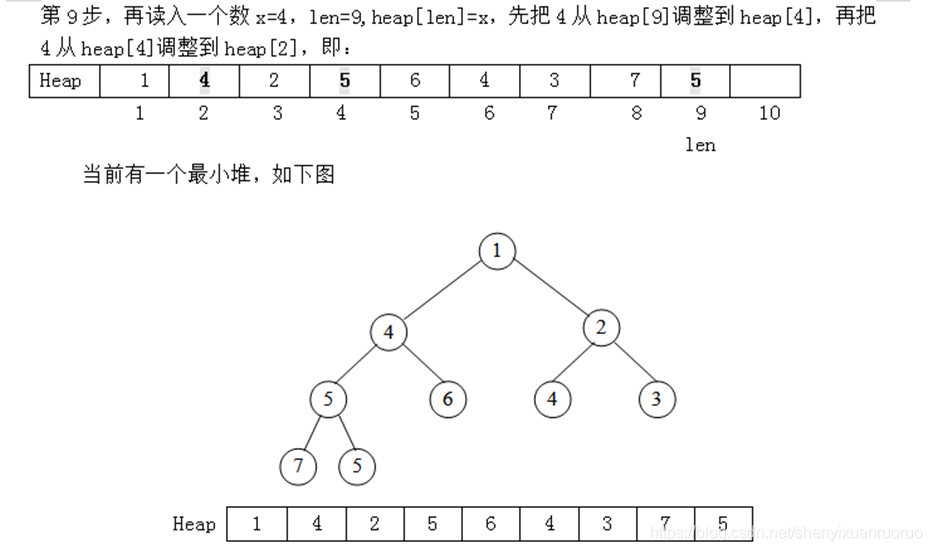
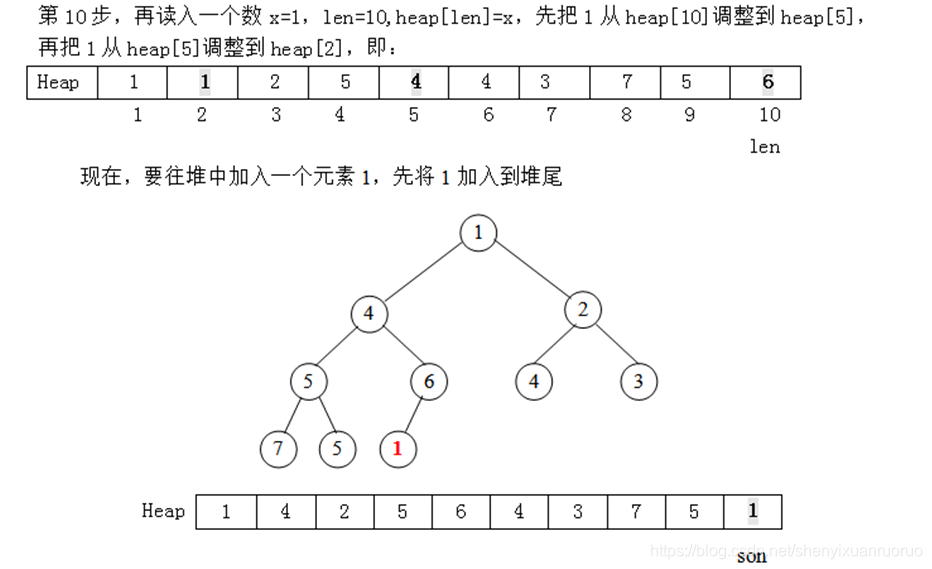
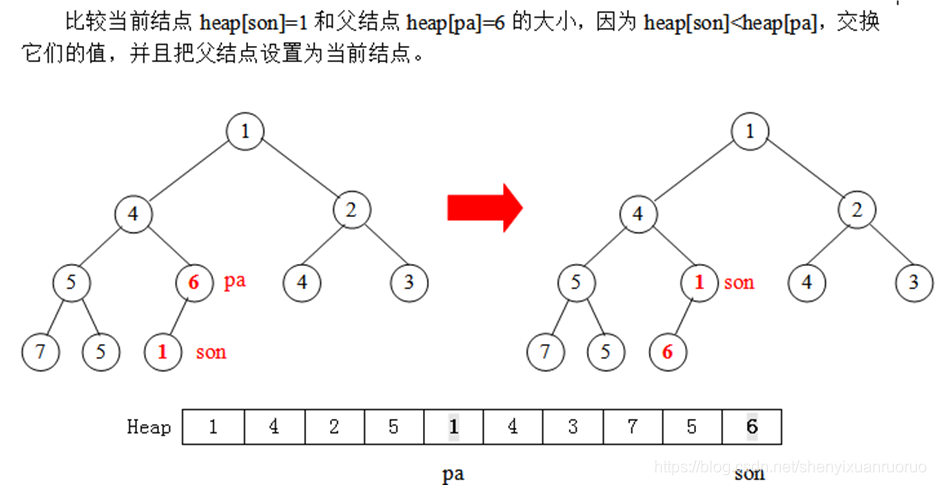
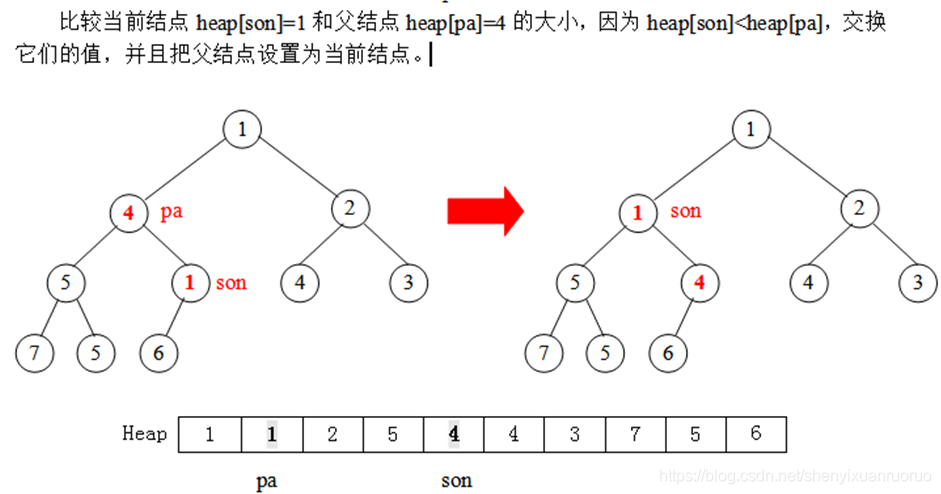
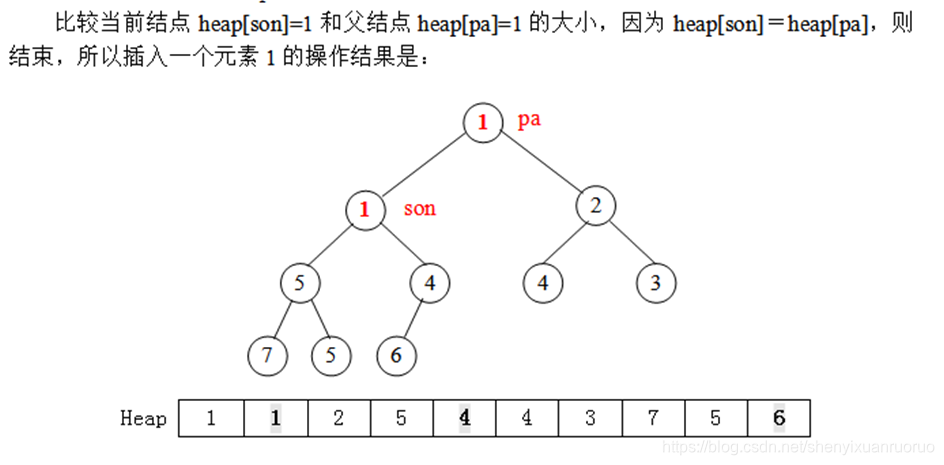
    实际上，我们也可以直接用完全二叉树的形式描述出这个过程，得到如下的一棵完全二叉树（堆）：

void put(int d)                 //heap[1]为堆顶
{
	int now, next;
	heap[++heap_size] = d;
	now = heap_size;
	while(now > 1)
	{
		next = now >> 1;
		if(heap[now] >= heap[next]) break;
		swap(heap[now], heap[next]);
		now = next;
	}
}

使用C++标准模板库STL（需要头文件<algorithm>）：

void put(int d)
{
	heap[++heap_size] = d;
	//push_heap(heap + 1, heap + heap_size + 1);            //大根堆
	push_heap(heap + 1, heap + heap_size + 1, greater<int>()); //小根堆
}

P党

procedure put(x:longint);
var
 son,tmp:longint;
begin
 len:=len+1;
 heap[len]:=x;
 son:=len;
 while (son<>1)and(heap[son div 2]>heap[son]) do
  begin
   tmp:=heap[son div 2];
   heap[son div 2]:=heap[son];
   heap[son]:=tmp;
   son:=son div 2;
  end;
end;

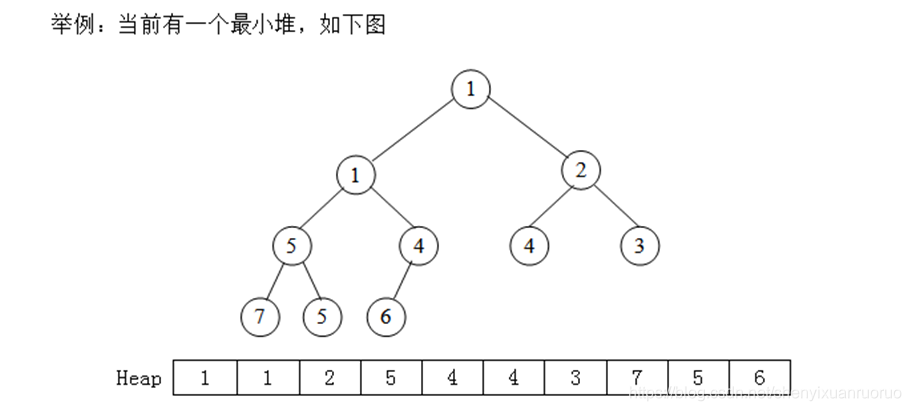
2、从堆中取出并删除一个元素的算法(get)如下：

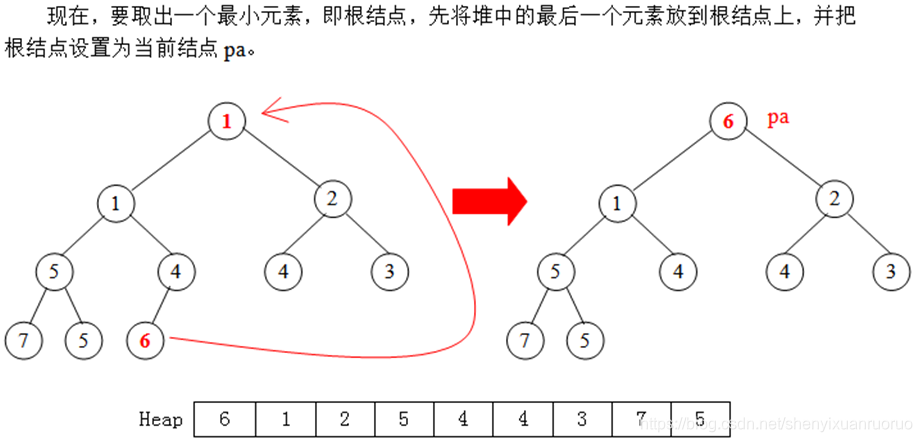
    （1）取出堆的根结点的值。
    （2）把堆的最后一个结点（len）放到根的位置上，把根覆盖掉。把堆
         的长度减一。
    （3）把根结点置为当前父结点pa。
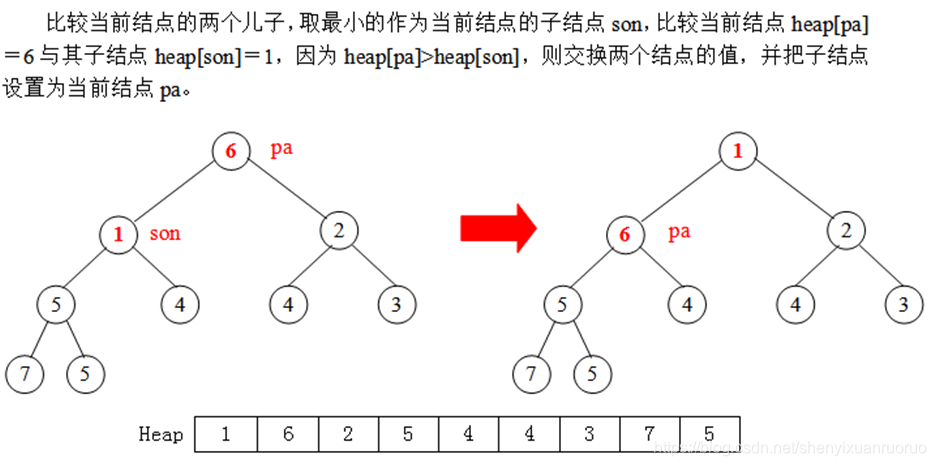
    （4）如果pa无儿子（pa>len/2），则转（6）；否则，把pa的两（或一） 
         个儿子中值最小的那个置为当前的子结点son。
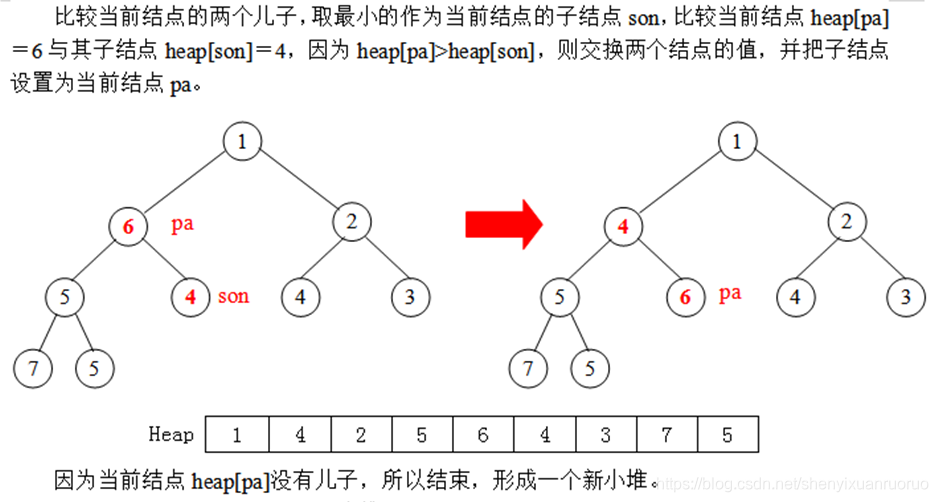
    （5）比较pa与son的值，如果fa的值小于或等于son，则转（6）；
         否则，交换这两个结点的值，把pa指向son，转（4）。
    （6）结束。

int get()                //heap[1]为堆顶
{
	int now=1, next, res= heap[1];
	heap[1] = heap[heap_size--];
	while(now * 2 <= heap_size)
	{
		next = now * 2;
		if (next < heap_size && heap[next + 1] < heap[next]) next++;
		if (heap[now] <= heap[next]) break;
		swap(heap[now], heap[next]);
		now = next;
	}
	return res;
}

使用C++标准模板库STL（需要头文件<algorithm>）：

int get()
{
	//pop_heap(heap + 1, heap + heap_size + 1);               //大根堆
	pop_heap(heap + 1, heap + heap_size + 1, greater<int>());    //小根堆
	return heap[heap_size--];
}

P党

function get:longint;
var
 fa,son,tmp:longint;
begin
 get:=heap[1];
 heap[1]:=heap[len];
 len:=len-1;
 fa:=1;
 while (fa*2<=len)or(fa*2+1<=len) do
  begin
   if (fa*2+1>len)or(heap[fa*2]<heap[fa*2+1])
    then son:=fa*2
    else son:=fa*2+1;
   if heap[fa]>heap[son] then
    begin
     tmp:=heap[fa];
     heap[fa]:=heap[son];
     heap[son]:=tmp;
     fa:=son;
    end
   else break;
  end;
end;

五、堆的应用

例1、合并果子(fruit)

    【问题描述】
    在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。
    每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过n-1次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。
    因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。
    例如有3种果子，数目依次为1，2，9。可以先将 1、2堆合并，新堆数目为3，耗费体力为3。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为12，耗费体力为 12。所以多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。
    【输入文件】
    输入文件fruit.in包括两行，第一行是一个整数n（1 <= n <= 30000），表示果子的种类数。第二行包含n个整数，用空格分隔，第i个整数ai（1 <= ai <= 20000）是第i种果子的数目。
    【输出文件】
    输出文件fruit.out包括一行，这一行只包含一个整数，也就是最小的体力耗费值。输入数据保证这个值小于231。

【样例一输入】

3
1 2 9

【样例一输出】

15

【样例二输入】

10

3 5 1 7 6 4 2 5 4 1

【样例二输出】

120

    【数据规模】
    对于30%的数据，保证有n <= 1000；
    对于50%的数据，保证有n <= 5000；
    对于全部的数据，保证有n <= 30000。
    【问题分析】
    1、算法分析
    将这个问题换一个角度描述：给定n个叶结点，每个结点有一个权值W[i]，将它们中两个、两个合并为树，假设每个结点从根到它的距离是D[i]，使得最终∑(wi * di)最小。
    于是，这个问题就变为了经典的Huffman树问题。Huffman树的构造方法如下：
    （1）从森林里取两个权和最小的结点；
    （2）将它们的权和相加，得到新的结点，并且把原结点删除，将新结点插入到森林中；
    （3）重复(1)~(2)，直到整个森林里只有一棵树。
    2、数据结构
    很显然，问题当中需要执行的操作是：(1) 从一个表中取出最小的数 (2) 插入一个数字到这个表中。支持动态查找最小数和动态插入操作的数据结构，我们可以选择用堆来实现。因为取的是最小元素，所以我们要用小根堆实现。
    用堆的关键部分是两个操作：put操作，即往堆中加入一个元素；get操作，即从堆中取出并删除一个元素。
    3、操作实现
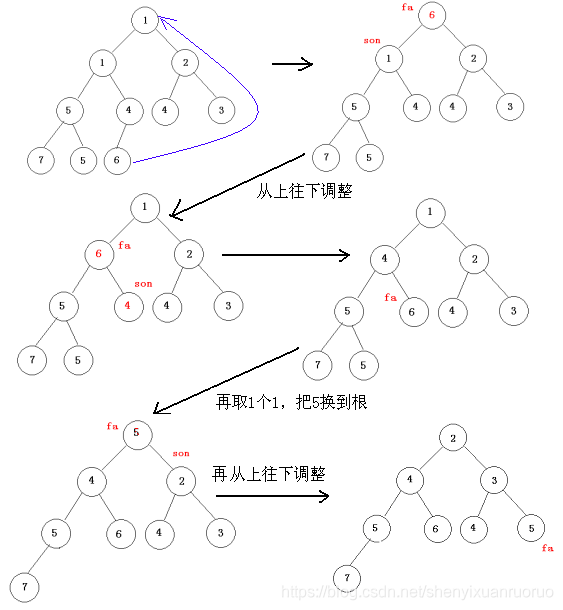
    整个程序开始时通过n次put操作建立一个小根堆，然后不断重复如下操作：两次get操作取出两个最小数累加起来，并且形成一个新的结点，再插入到堆中。如1+1=2，再把2插入到堆的后面一个位置，然后从下往上调整，使得包括2在内的数组满足堆的性质即：

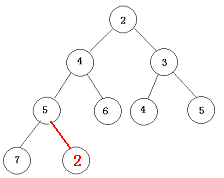
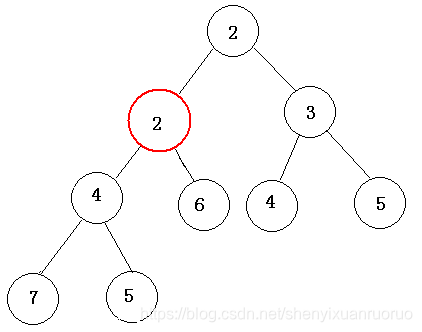
    get和put操作的复杂度均为log2n。所以建堆复杂度为nlog2n。合并果子时，每次需要从堆中取出两个数，然后再加入一个数，因此一次合并的复杂度为3log2n，共n-1次。所以整道题目的复杂度是nlog2n。

【参考程序】

#include <iostream>
#include <cstdio>
using namespace std;
int heap_size, n;
int heap[30001];
void swap(int &a, int &b)  //加&后变量可修改
{
	int t = a;a = b;b = t;
}
void put(int d)
{
	int now, next;
	heap[++heap_size] = d;
	now = heap_size;
	while(now > 1)
	{
		next = now >> 1;
		if(heap[now] >= heap[next])return;
		swap(heap[now], heap[next]);
		now = next;
	}
}
int get()
{
	int now, next, res;
	res = heap[1];
	heap[1] = heap[heap_size--];
	now = 1;
	while(now * 2 <= heap_size)
	{
		next = now * 2;
		if(next < heap_size && heap[next + 1] < heap[next])next++;
		if(heap[now] <= heap[next])return res;
		swap(heap[now], heap[next]);
		now = next;
	}
	return res;
}
void work()
{
	int i, x, y, ans = 0;
	cin >> n;
	for(i = 1 ; i <= n ; i++)          //建堆，其实直接将数组排序也是建堆方法之一
	{
		cin >> x;
		put(x);
	}
	for(i = 1 ; i < n ; i++)           //取、统计、插入
	{
		x = get();
		y = get();                //也可省去这一步，而直接将x累加到heap[1]然后调整
		ans += x + y;
		put(x + y);
	}
	cout << ans << endl;
}

int main()
{
	freopen("fruit.in", "r", stdin);
	freopen("fruit.out", "w", stdout);
	ios::sync_with_stdio(false);      //优化。打消iostream的输入输出缓存，使得cin cout 时间和printf scanf 相差无几
	work();
	return 0;
}

使用C++标准模板库STL：
 

#include <iostream>
#include <queue>
#include <cstdio>
using namespace std;
int n;
priority_queue<int,vector<int>,greater<int> > h;     //优先队列 

void work()
{
	int i, x, y, ans = 0;
	cin >> n;
	for(i = 1 ; i <= n ; i++)                      //建堆
	{
		cin >> x;
		h.push(x);
	}
	for(i = 1 ; i < n ; i++)                       //取、统计、插入
	{
		x = h.top();h.pop();
		y = h.top();h.pop();
		ans += x + y;
		h.push(x + y);
	}
	cout << ans << endl;
}

int main()
{
	freopen("fruit.in", "r", stdin);
	freopen("fruit.out", "w", stdout);
	work();
	return 0;
}

P党

var
 len,n,i,tmp,a,b,ans:longint;
 heap:array[0..30000] of longint;
procedure put(x:longint);
var
 son,tmp:longint;
begin
 len:=len+1;
 heap[len]:=x;
 son:=len;
 while (son<>1)and(heap[son div 2]>heap[son]) do
  begin
   tmp:=heap[son div 2];
   heap[son div 2]:=heap[son];
   heap[son]:=tmp;
   son:=son div 2;
  end;
end;
function get:longint;
var
 fa,son,tmp:longint;
begin
 get:=heap[1];
 heap[1]:=heap[len];
 len:=len-1;
 fa:=1;
 while (fa*2<=len)or(fa*2+1<=len) do
  begin
   if (fa*2+1>len) or (heap[fa*2]<heap[fa*2+1])
    then son:=fa*2
    else son:=fa*2+1;
   if heap[fa]>heap[son] then
    begin
     tmp:=heap[fa];
     heap[fa]:=heap[son];
     heap[son]:=tmp;
     fa:=son;
    end
   else break;
  end;
end;
begin
 read(n);
 for i:=1 to n do
  begin
   read(tmp);
   put(tmp);
  end;
 for i:=1 to n-1 do
  begin
   a:=get;
   b:=get;
   ans:=ans+a+b;
   put(a+b);
  end;
 writeln(ans);
end.

例2、堆排序(heapsort)

【问题描述】
    假设n个数存放在A[1..n]中，我们可以利用堆将它们从小到大进行排序，这种排序方法，称为“堆排序”。输入两行，第1行为n，第2行为n个整数，每个数之间用1个空格隔开。输出1行，为从小到大排好序的n个数，每个数之间也用1个空格隔开。
【问题分析】
    一种思路是完全按照上一个例题的方法去做。

【参考程序1】

#include <iostream>
#include <cstdio>
using namespace std;
int heap_size, n;
int heap[100001];
void swap(int &a, int &b)
{
	int t = a;a = b;b = t;
}

void put(int d)
{
	int now, next;
	heap[++heap_size] = d;
	now = heap_size;
	while(now > 1)
	{
		next = now >> 1;
		if(heap[now] >= heap[next])return;
		swap(heap[now], heap[next]);
		now = next;
	}
}
int get()
{
	int now, next, res;
	res = heap[1];
	heap[1] = heap[heap_size--];
	now = 1;
	while(now * 2 <= heap_size)
	{
		next = now * 2;
		if(next < heap_size && heap[next + 1] < heap[next])next++;
		if(heap[now] <= heap[next])return res;
		swap(heap[now], heap[next]);
		now = next;
	}
	return res;
}

void work()
{
	int i, x, y, ans = 0;
	cin >> n;
	for(i = 1 ; i <= n ; i++)
	{
		cin >> x;
		put(x);
	}
	for(i = 1 ; i < n ; i++) cout << get() << ' ';
	cout << get() << endl;
}

int main()
{
	freopen("heapsort.in", "r", stdin);
	freopen("heapsort.out", "w", stdout);
	work();
	return 0;
}

    另一种思路是考虑这样两个问题，一是如何构建一个初始（大根）堆？二是确定了最大值后（堆顶元素A[1]即为最大值），如何在剩下的n-1个数中，调整堆结构产生次大值？
    对于第一个问题，我们可以这样理解，首先所有叶结点（编号为N/2+1到N）都各自成堆，我们只要从最后一个分支结点（编号为N/2）开始，不断“调整”每个分支结点与孩子结点的值，使它们满足堆的要求，直到根结点为止，这样一定能确保根（堆顶元素）的值最大。“调整”的思想如下：即如果当前结点编号为i, 则它的左孩子为2*i, 右孩子2*i+1,首先比较A[i]与MAX（A[2*i]，A[2*i+1]）；如果A[i]大，说明以结点i为根的子树已经是堆，不用再调整。否则将结点i和左右孩子中值大的那个结点j互换位置，互换后可能破坏以j为根的堆所以必须再比较A[j] 与MAX（A[2*j]，A[2*j+1]）,依此类推，直到父结点的值大于等于两个孩子或出现叶结点为止。这样，以i为根的子树就被调整成为一个堆。
    编写的子程序如下：

　　void heap(int r[], int nn, int ii)//一次操作，使r满足堆的性质，得到1个最大数在r[ii]中
　　{
	      int x, i=ii, j;
	      x = r[ii];   //把待调整的结点值暂存起来
	      j = 2 * i;     //j存放i的孩子中值大的结点编号，开始时为i的左孩子编号
	      while(j <= nn) //不断调整，使以i为根的二叉树满足堆的性质
	        {
	            if(j < nn && r[j] < r[j + 1]) j++; //若i有右孩子且值比左孩子大，则把j设为右孩子的编号
	            if(x < r[j]) //若父结点比孩子结点小，则调整父结点和孩子结点中值大的那个结点，确保此处满足堆的性质
　　	{
　　	    r[i] = r[j];
　　	    i = j;
　　	    j = 2 * i;
　　	}
　　         else j = nn + 1;  //故意让j超出范围，终止循环
　　    }
　        r[i] = x;             //调整到最终位置
　　}

    经过第一步骤建立好一个初始堆后，可以确定堆顶元素值最大，我们就把它A[1]与最后一个元素A[N]交换，然后再对A[1..N-1]进行调整，得到次大值与A[N-1]交换，如此下去，所有元素便有序存放了。
    主程序的框架如下：
【参考程序2】

int a[100001];
int i,temp,n;
int main()
{
  输入n和n个元素；
　for(i=n / 2 ; i >= 1 , i--)
     heap(a,n,i)；         //建立初始堆，且产生最大值A[1]}
  for(i=n ; i >= 2 ; i--)  //将当前最大值交换到最终位置上，再对前i-1个数调整
    {                                    
      swap(a[1],a[i]);
      heap(a,i-1,1)；
    }
  输出；
  return 0;
}

P党

var
 len,n,i,tmp:longint;
 heap:array[0..101] of longint;
procedure put(x:longint);
var
 son,tmp:longint;
begin
 len:=len+1;
 heap[len]:=x;
 son:=len;
 while (son<>1)and(heap[son div 2]>heap[son]) do
  begin
   tmp:=heap[son div 2];
   heap[son div 2]:=heap[son];
   heap[son]:=tmp;
   son:=son div 2;
  end;
end;
function get:longint;
var
 fa,son,tmp:longint;
begin
 get:=heap[1];
 heap[1]:=heap[len];
 len:=len-1;
 fa:=1;
 while (fa*2<=len)or(fa*2+1<=len) do
  begin
   if (fa*2+1>len) or (heap[fa*2]<heap[fa*2+1])
    then son:=fa*2
    else son:=fa*2+1;
   if heap[fa]>heap[son] then
    begin
     tmp:=heap[fa];
     heap[fa]:=heap[son];
     heap[son]:=tmp;
     fa:=son;
    end
   else break;
  end;
end;
begin
 read(n);
 for i:=1 to n do
  begin
   read(tmp);
   put(tmp);
  end;
 for i:=1 to n-1 do
  write(get,' ');
 writeln(get);
end.

【小结】
    堆排序在数据较少时并不值得提倡，但数据量很大时，效率就会很高。因为其运算的时间主要消耗在建立初始堆和调整过程中，堆排序的时间复杂度为O（nlog2n），而且堆排序只需一个供交换用的辅助单元空间，是一种不稳定的排序方法。

zzruoruo
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值