【优化】logistic和softmax代价函数

这两种代价函数都能够把$(-\infty ,\infty )$上的误差/置信度/代价映射到$(0,1)$之间。

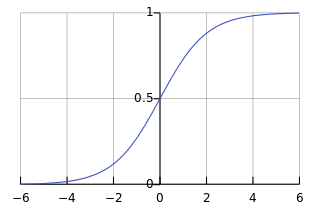
logistic函数

输入为标量$z$
$$\sigma (z)=\frac{e^z}{1+e^z}=\frac{1}{1+e^{-z}}$$

常用于二分类问题的代价项。也称为sigmoid函数。

softmax函数

输入为矢量z={zk}k=1:Kz=\{z_k\}_{k=1:K}z={zk​}k=1:K​
$$\sigma (z{)}_k=\frac{e^{z_k}}{{\Sigma }_{k=1}^K{e}^{z_k}}$$

常用于多类分类问题的代价项。

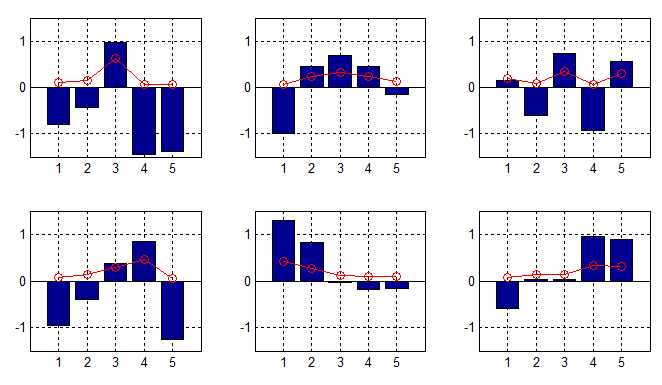
下图示出$K=5$时，softmax函数的输入（蓝色柱）和输出（红色曲线）