剑指Offer：链表中环的入口节点

题

题目描述
给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null。

解

非常非常非常基础的一道题目了。但实话讲我一直不明白我会写的那种方法为什么是正确的。现证明之。
来自牛客网大佬的解答。参考链接见下，解释见下。

链接：https://www.nowcoder.com/questionTerminal/253d2c59ec3e4bc68da16833f79a38e4
来源：牛客网

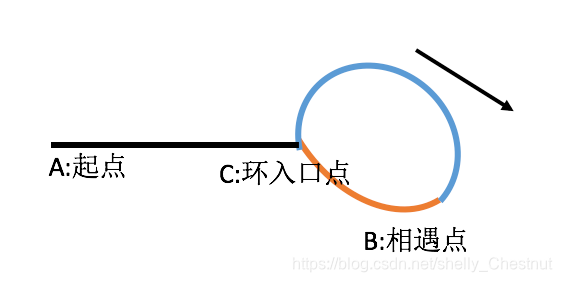
假设x为环前面的路程（黑色路程），a为环入口到相遇点的路程（蓝色路程，假设顺时针走）， c为环的长度（蓝色+橙色路程）
当快慢指针相遇的时候：

此时慢指针走的路程为Sslow = x + m * c + a
快指针走的路程为Sfast = x + n * c + a
2 Sslow = Sfast
2 * ( x + m*c + a ) = (x + n *c + a)
从而可以推导出：
x = (n - 2 * m )*c - a
= (n - 2 *m -1 )*c + c - a
即环前面的路程 = 数个环的长度（为可能为0） + c - a
什么是c - a？这是相遇点后，环后面部分的路程。（橙色路程）
所以，我们可以让一个指针从起点A开始走，让一个指针从相遇点B开始继续往后走，
2个指针速度一样，那么，当从原点的指针走到环入口点的时候（此时刚好走了x）
从相遇点开始走的那个指针也一定刚好到达环入口点。
所以2者会相遇，且恰好相遇在环的入口点。

最后，判断是否有环，且找环的算法复杂度为：

时间复杂度：O(n)

空间复杂度：O(1)

    public ListNode EntryNodeOfLoop(ListNode pHead){
        // 老生常谈
        if(pHead == null) return pHead;
        ListNode fast = pHead, slow = pHead;
        while(fast.next != null){
            fast = fast.next.next;
            slow = slow.next;
            if(fast == slow) break;
        }
        if(fast.next == null) return null;
        slow = pHead;
        while(slow != fast){
            fast = fast.next;
            slow = slow.next;
        }
        return fast;
    }