递归回溯类别的小游戏，有了和同学吹牛的资本了ʅ（´◔౪◔）ʃ

//递归调用应用实例------迷宫问题
public class Test03 {
    public static void main(String[] args) {
        //思路：1.创建迷宫 8*7大小int[][] map = new int[8][7];
        //2.规定 0为通路，1为障碍物
        int[][] map = new int[8][7];
        //3.将迷宫的最上/下/左/右方 设置为障碍物
        for (int i = 0; i < 7; i++) {//将第一行和最后一行全部设置为1(障碍物)
            map[0][i] = 1;
            map[7][i] = 1;
        }
        for (int j = 0; j < 7; j++) {//将第一列和最后一列全部设置为1(障碍物)
            map[j][0] = 1;
            map[j][6] = 1;
        }
       /* //设置迷宫内的障碍物(1)
        map[5][4] = 1;
        map[5][5] = 1;
        map[5][6] = 1;
        map[6][4] = 1;
        map[6][6] = 1;
        map[7][4] = 1;*/
       /* //设置迷宫内的障碍物(2)
        map[6][5] = 1;
        */
        //设置迷宫内的障碍物(3)
        map[2][4] = 1;
        map[4][3] = 1;
        map[5][2] = 1;
        map[5][4] = 1;
        map[5][4] = 1;
        map[6][2] = 1;
        //遍历输出数组
        System.out.println("=======当前地图的样貌=======");
        for (int i = 0; i < map.length; i++) {
            for (int j = 0; j < map[i].length; j++) {
                System.out.print(map[i][j] + "\t ");
            }
            System.out.println();
        }
        //下面调用T类，创造 mouse对象
        T mouse = new T();
        mouse.findway(map,1,1);
        System.out.println("找路的情况");
        System.out.println();
        System.out.println("打印小鼠的寻找路径，2表示路径");
        for (int i = 0; i < map.length; i++) {
            for (int j = 0; j < map[i].length; j++) {
                System.out.print(map[i][j] + "\t ");
            }
            System.out.println();
        }

    }
}
class T{
    //使用递归回溯的方法解决问题，findway用来找路
    //找到返回true 没找到返回false
    //i,j是小鼠得位置，  初始位置是1，1
    //0表示当前可以走，1表示障碍物，不能走，2表示找到出口，3表示走过，
    // 但是走不通是死路
    //map[6][5]表示找到了出口，退出迷宫
    //确定思路，下，右，上，左(可以根据实际情况进行改变)


    public boolean findway(int[][] map,int i,int j) {//使用布尔类型的方法，通过true || false判断是否为通路
        if(map[6][5] == 2) {//首先设置[6][5]的位置为出口
            return true;
        }else{
            if(map[i][j]==0) {//若当前可以走
                map[i][j] = 2;//先假设当前位置为通路可以走得通

            if(findway(map, i+1, j)){//向下移动
                return true;//大概解释一下，这里的意思是如果要移动的位置走的通，不为1，就移动到该位置，如果不通，就走else-if的方法
            } else if (findway(map,i,j+1)) {//向右移动
                return true;
            }else if(findway(map, i-1, j)){//向上移动(这种情况是，如果进入了死胡同，下左右都走不动，返回向上)
                return true;
            }else if(findway(map, i, j-1)){//向左移动
                return true;
            }else {
                map[i][j] = 3;//3表示走过，但是走不通
                return false;//返回false
            }

        }else{//这种情况是找完了，找不到[6][5]出口，或者到不了[6][5]出口的情况
                //map[i][j] = 1,3的情况
            return false;
            }
        }

    }
}

解读：

1.迷宫实际上就是一个简单的二维数组，由你来决定迷宫的大小，(这里要注意了，数组的元素是从零开始的，也就是要注意溢出的问题)，设置好出口以及障碍物的位置，就可以开始找出口了。

2.findway方法使用了一次，if的嵌套使用，外层第一步的意思是出口设置为[6][5],找到了就返回true,否则就是找不到出口或者map[i][j] = 1,3的情况

3.内层第一步：表示当前的位置可以走，设置为0，假设该位置是通路(2)，通过下右上左的形式，寻找出路，走得通规定为2，走过但走不通规定为3，(具体内容可以看注释)。

二、汉诺塔

图片展示：

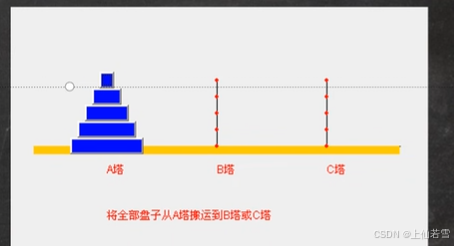
规则：1.将所有的盘子从A塔移动到C塔

2.大的盘子不能放到小盘子的上面

3.尽量用最少的步数达到目标。

代码展示：

import java.util.Scanner;

public class Test05 {
    public static void main(String[] args) {

T2 you = new T2();
Scanner sc = new Scanner(System.in);
System.out.print("请输入你要移动的盘子的个数：");
int num  = sc.nextInt();
you.move(num,'A','B','C');
System.out.println("你一共需要移动"+you.getCount()+"步");

    }
}
//创建T2类，用来实现盘子的转移
class T2{
    int count = 0;
    public void move(int i,char a,char b,char c){//i表示要移动盘子的个数，a,b,c的意思是指，a是起始塔，c是目标塔 借助b进行传递
        if(i==1){
            System.out.println(a+"->"+c);
            count++;
        }else{//如果要移动的盘子的数量不为1，则进行回溯
            //可以将盘子看作(最下面的盘子0)和(它上面的所有盘子1)的结合体
            move(i-1,a,c,b);//先将盘子1移动从a塔移动到b塔，借助c塔
           count++;
            System.out.println(a+"->"+c);//再将最下面的盘子0 移动到c塔
            move(i-1,b,a,c);//再将1的盘子从b塔运送到c塔，借助a塔
            //System.out.println(number);
        }

    }
    public int getCount(){
        return count;
    }


}

解读：1.首先要确定盘子的起始位置，中间的移动需要借助哪个塔。

2.整体的盘子应该视为两个部分，一是最下面的盘子。二是以上的所有盘子。

3.移动的过程其实就是多次回溯，先将小的移到c,再移动到b，……诸如此类进行。

三、八皇后

介绍和规则：八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击即：任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

上图：

代码：

public class Test06 {
        //定义能放置的最大的皇后的个数
        int queenMax = 8;
        //设置放置的次数
        int num = 0;
        //定义一个数组，用于存放皇后位置的结果
        int[] arr = new int[queenMax];
        public static void main(String[] args){
            Test06 queen = new Test06();
            queen.checkWay(0);//从第一个皇后开始放
            System.out.println("一共有"+queen.num+"种解法！");

        }
        public void checkWay(int n){
            if(n == queenMax){
//n=8,说明将要放置第九个皇后了，打印当前所有的的位置
                print();
                return;
            }
//依次放入皇后，并判断是否冲突
            for(int i = 0;i<queenMax;i++){
//先把皇后n放到第一排
                arr[n] = i;
//放置到第n个皇后时是否冲突
                if(judge(n)){
//不冲突，接着放n+1,开始递归
                    checkWay(n+1);
                }
            }
        }
        public boolean judge(int n){
            for(int i = 0;i<n;i++){
                if(arr[i] == arr[n]||Math.abs(arr[n]-arr[i])==Math.abs(n-i)){
                    return false;
                }
            }
            return true;
        }
        //写一个方法可以将皇后的位置输出
        public void print(){
            num++;
            for(int i =0;i<arr.length;i++){
                System.out.print(arr[i]+"\t");
            }
            System.out.println();
        }
    }

解读：三个主要的方法1.checkway():检查皇后的移动路线，

2.judge() 判断放置的皇后的位置是否满足规则。

3.print(),打印当前皇后的位置以及一共的解法 num.

4.依次按照顺序的方法放置皇后的位置，先放到第一排……，以此类推，放一个，检查一次（judge()）,再使用(checkway())的方法放置下一个皇后的位置。