卡尔曼滤波（2）——多维卡尔曼滤波

  上篇文章中我们以一维卡尔曼滤波作为例子简单介绍了卡尔曼滤波，那么如果要滤波的量不仅一个而是多个呢？

一维卡尔曼滤波

sdff20201029，公众号：萌萌哒程序猴卡尔曼滤波（1）

  本文以卡尔曼跟踪为例子介绍多维卡尔曼滤波的计算过程。卡尔曼跟踪通常以目标检测网络输出的检测框作为输入，然后进行预测、匹配、更新等步骤（匹配算法常见有匈牙利匹配、GS匹配、暴力匹配等，本文不做详细介绍，之后的文章会做专门介绍）。

一、明确观测量和状态量

  检测框就是卡尔曼滤波的输入测量值，其主要信息包含左上角x、y坐标，以及矩形框的宽w、高h。观测量通常取矩形框的中心坐标和宽高w、h：

Z=[cx,cy,w,h]^T

cx=x+w/2

cy=y+h/2

  当然，卡尔曼滤波的状态量也是围绕这几个量来设置的。基于卡尔曼滤波的跟踪方法一般有两种状态量，本文主要介绍第（1）种。

（1）X=[cx,cy,w,h,vx,vy,vw,vh]^T

  其中：

cx——矩形框x方向中心点，cx=x+w/2

cy——矩形框y方向中心点，cy=y+h/2

w——矩形框像素宽度

h——矩形框像素高度

vx——cx的变化量

vy——cy的变化量

vw——w的变化量

vh——h的变化量

（2）X=[cx,cy,s,r,vx,vy,vs,vr]^T

  其中：

cx——矩形框x方向中心点，cx=x+w/2

cy——矩形框y方向中心点，cy=y+h/2

s——矩形框面积，s=w*h

r——矩形框宽高比，r=w/h

vx——cx的变化量

vy——cy的变化量

vs——s的变化量

vr——r的变化量

二、明确观测矩阵H

  由上述可知观测量Z和状态量X呈线性关系（Z=HX），得到观测矩阵为：

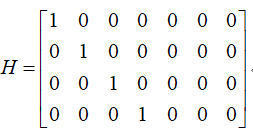
三、明确状态转移方程

  假设状态量的各分量都符合线性规律，那么由k-1时刻的状态量预测k时刻状态量为：

  根据上式，可得到状态转移方程：

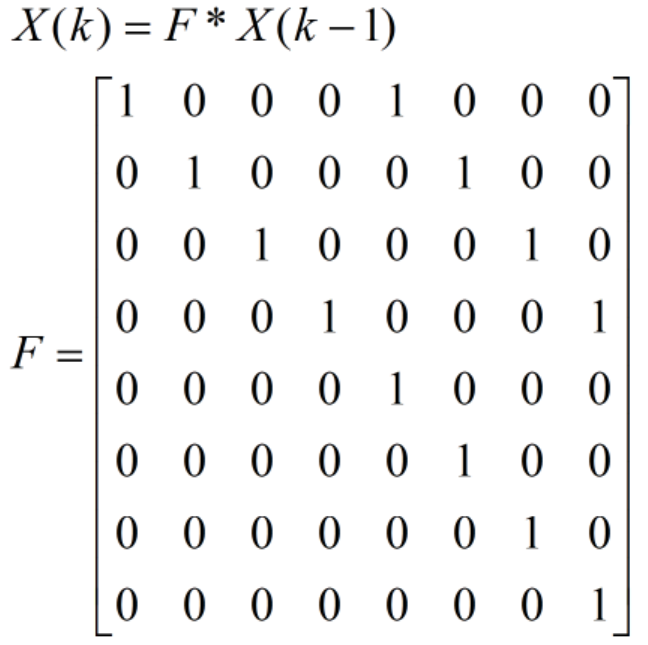
四、明确Q矩阵和R矩阵

  （1）Q为过程噪声协方差矩阵，Q为对角阵，Q的维度由状态量X的维度决定：X维度为8*1，那么Q的维度为8*8。Q由测量过程中各种噪声叠加综合决定：叠加噪声的方差越大，则Q应设置为越小值（也即Q值越小，滤波越平滑越滞后）。

  （2）R为测量噪声协方差矩阵，R也为对角阵，R的维度由观测量Z的维度决定：Z维度为4*1，那么R的维度为4*4。R由传感器自身决定，比如相机出厂时自身参数会包含其噪声方差：传感器自身的噪声方差越大，则R应设置为越大值（也即R值越大，滤波越平滑越滞后）。

  卡尔曼跟踪的应用场景中，通常固定R矩阵，本人根据经验通常把R的对角值固定设置为0.1。

  

  动态调整Q矩阵，一般将Q的对角值初始化为较小值。本人根据经验通常把Q的对角值初始化为0.001，跟踪过程中再动态调整。常用的动态调整Q对角值策略为：卡尔曼更新跟踪框之后，计算匹配检测框与跟踪框的iou重叠度，如果重叠度小于阈值，说明跟踪框滞后了，此时把Q的对角值调大以减小滞后，反之则调小Q的对角值。

五、误差协方差矩阵P的初始化

  误差协方差矩阵P是卡尔曼滤波过程中用于表示估计值误差的矩阵，也即表示系统状态估计值的不确定程度，该矩阵在滤波过程中动态调整，使用测量残差对其进行动态更新。

  矩阵P的维度由状态量X的维度决定，假如X的维度为8*1，那么P的维度就是8*8的对角矩阵。滤波开始之前，需要对矩阵P进行初始化，通常将对角值初始化为0.1或较小值：

六、卡尔曼预测

  卡尔曼预测主要步骤是根据上一帧的跟踪框来预测当前帧的跟踪框，并更新矩阵P：

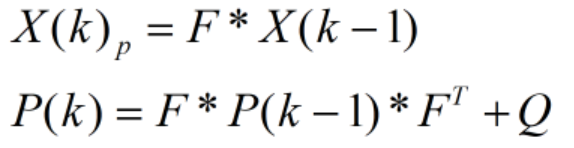
七、预测框与检测框的匹配

  本文暂时不介绍匹配算法。但在此说明一下为什么要做匹配：在多目标跟踪中，检测框作为输入的测量值，通常有多个检测框输入，对应的预测跟踪框也有多个，需要先确认检测框和预测跟踪框的一一对应关系之后才能知道用哪个检测框来更新哪个跟踪框。

八、卡尔曼更新

  卡尔曼更新步骤主要做的是把预测值与测量值进行加权融合。

  （1）计算加权的权重K。

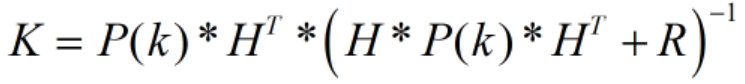
  （2）更新状态量。

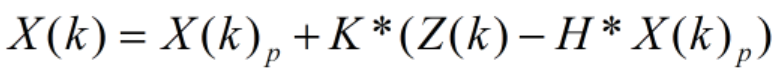
  （3）再更新矩阵P。

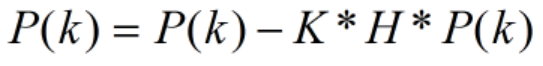
  好了，本文就介绍到这里。本文就先不上代码了，之后介绍完卡尔曼系列了再详细讲些代码。有什么疑问，欢迎留言讨论，多谢大家支持！