1. 简介
在上一期的文章中,我们对线性倒立摆在2D平面内的运动过程进行了分析,并给出了基于轨道能量的线性倒立摆控制过程。
在本期文章中,我们将建立线性倒立摆模型的运动学模型,为后面进行倒立摆的仿真控制铺垫基础。最终,我们可以使用所构建的运动学模型控制倒立摆模型的末端机构来绘制心形图案,源代码已开源,详见文末。
在Python中使用绘图工具绘制的结果:

在VREP(CoppeliaSim)中的仿真结果:

2. 倒立摆运动学模型构建
2.1 关节坐标系
在后续的仿真过程中,我们将先使用线性倒立摆模型进行二维矢状面内的仿真控制,然后再扩展到三维。本文使用的线性倒立摆模型如下:

模型一共包含4个关节(Left_hip, Left_knee, Right_hip, Right_knee),当然,在腿的末端还有两个foot,可以用于安装压力传感器。其中:
髋关节为旋转关节,可以控制模型的腿进行前后摆动;
膝关节为伸缩关键(线性运动关节),可以控制腿长。
为了方便后续扩展到三维环境,我们在构建运动学模型的时候保留了髋关节的内收/外展关节,只是在本文中内收/外展关节被锁死,后面在三维仿真的时候再打开。用于构建倒立摆运动学模型的方法来源于书籍《仿人机器人》介绍的方法,我们将倒立摆模型的各个关节的局部坐标系在空间中的相对关系建模如下:

在世界坐标系 中,以质心构建质心M所在的坐标系为root坐标系,然后依次构建两条腿的髋关节、膝关节和踝关节坐标系。蓝色的箭头表示该关节的运动方向,例如,每一个髋关节包括两个关节(FE:屈曲/伸展,AD:内收/外展),膝关节为线性关节(平移关节,Prismatic joint),由于本文中,倒立摆模型的踝关节等同于足底,因此踝关节坐标系等同于足底的坐标系。
2.2 正运动学模型
我们将各个关节之间的结构关系构建为树形结构,这样方便我们在编程的时候使用递归方法:

为了方便表示,我们给每个关节取一个名字,质心表示为BODY,其余关节依次命名为J1-J4。
正运动学模型的构建过程就是建立各个关节、连杆的局部坐标系,并求解各个关节之间的旋转、平移关系的过程。本文不打算详细介绍旋转、平移等基本过程的推导过程,如果读者不了解机器人学中基本的坐标变换过程,需要自行补充基础知识。这里我们也没有采用最常见的DH法来构建模型,而是采用了《仿人机器人》中提出的一种用于仿人机器人的运动学模型构建方法(类似于指数积,但作者没有命名该方法),我们这里做一个简单的介绍。
单个连杆的情况:
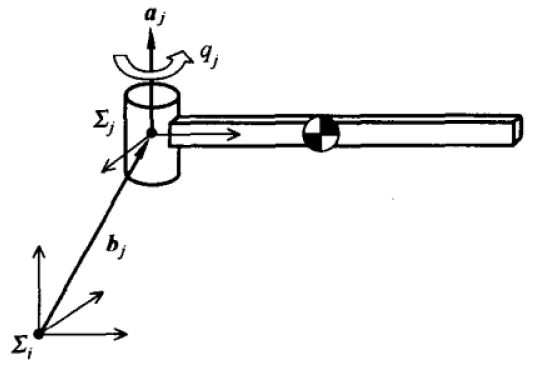
假设,对于第 个连杆的局部坐标系 来说,其母连杆的坐标系为 。设在母连杆的坐标系中,该连杆的转动轴矢量(即该关节绕哪个坐标轴旋转)为 , 的原点为 ,关节角为 ,当关节角为 时,连杆处于初始状态,姿态矩阵为 。
相对于其母连杆的齐次变换矩阵为
其中, ,表示罗德里格斯式(Rodrigues),该式子是本方法的核心,详细的推导过程见原书内容。
对于两个连杆的情况:

设母连杆的绝对位置和姿态分别为 和 ,则 的齐次变换矩阵为:
其中, 。
根据链式法则,我们可以求得:
综合前面的式子,我们可以得到第 个连杆 的位置和姿态:
这部分的代码在Python中的实现为:
def forwardKinematics(self, j=1):
if j == 0:
return
link = self.link_group.get(j)
if j != 1: # j=1 means BODY Link
i = link.mother
link_mother = self.link_group.get(i)
link.p = np.dot(link_mother.R, link.b) + link_mother.p
link.R = np.dot(link_mother.R, Rodrigues(link.a, link.q))
self.forwardKinematics(link.sister)
self.forwardKinematics(link.child
在构建了两个连杆的基本关系解算过程以后,我们就可以根据前面所阐述的倒立摆模型各个关节的局部坐标系以及结构关系来构建倒立摆模型的正运动学模型,这里不再详细阐述,详见源代码。
2.3 逆运动学模型
正运动学模型用于求解关节空间到任务空间的转换关系,逆运动学模型则相反,用于求解任务空间到关节空间的转换关系。如下图所示:

倒立摆模型在平地上做摆动运动的过程中,初始位置为直立状态,即 。那么,在运动过程中,已知质心的位置 和腿的末端foot的位置 ,则我们可以通过下面两个式子求解得到转角 和腿长 。
髋关节的转动角度即 :
而膝关节的平移距离即 与腿长的差值:
这样,我们只需要给定当前质心的位置和双脚的位置,即可求出四个关节的运动角度。
3. 仿真过程
正运动学的仿真过程比较简单,这里我们不展示结果,源代码中可以找到测试的demo。逆运动学的仿真中,我们分别给定双腿末端的运动轨迹,来合作实现心形图案的绘制。心形图形的绘制函数为:
绘制出来的结果为:

由于倒立摆模型的腿长有限,因此,我们可以通过在 的前面添加缩放常数将心形曲线缩放为符合倒立摆模型实际尺寸的结果,将心形曲线的值按照时间 作为倒立摆逆运动学模型的输入,则我们可以得到髋膝关节随时间变化的运动角度。
在Python中的仿真结果分别如下。
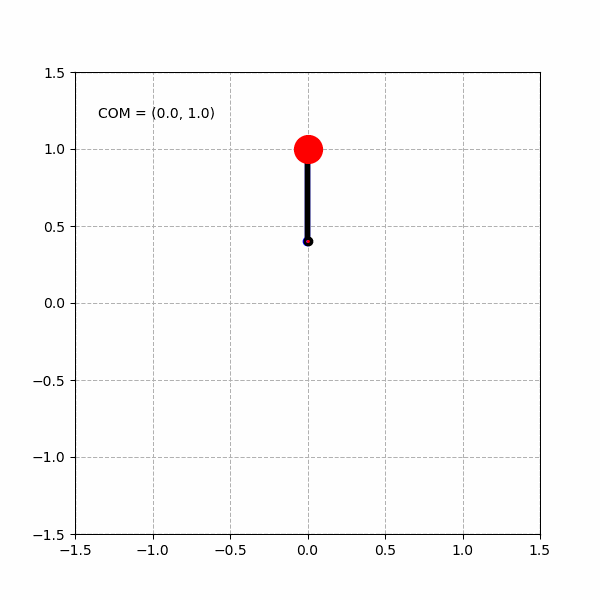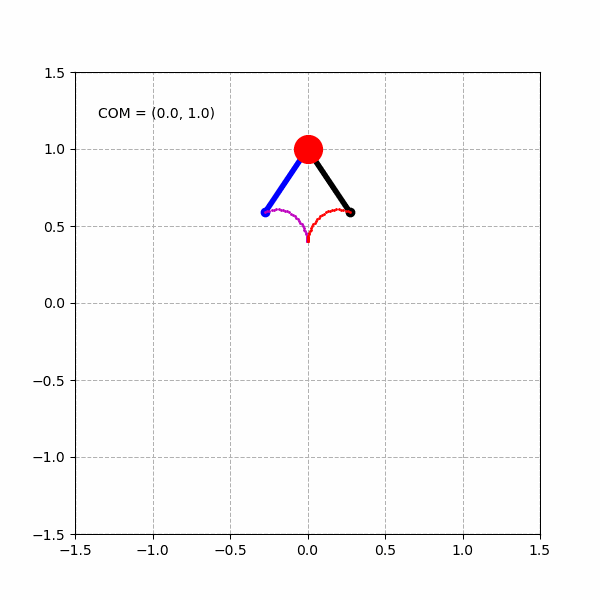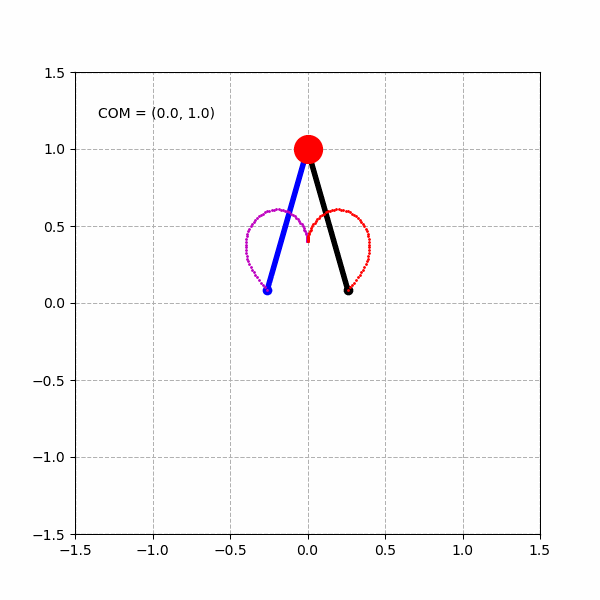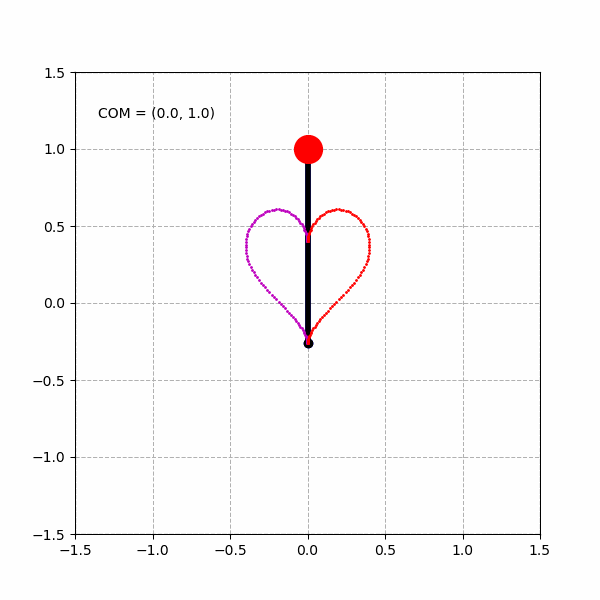
绘制单个心形曲线:
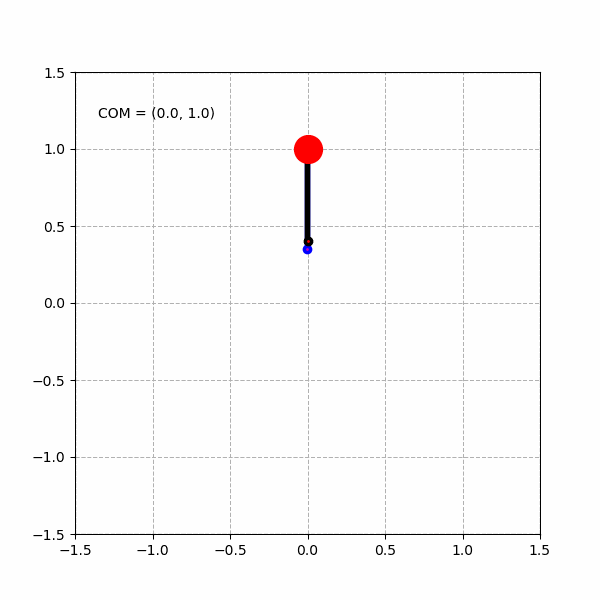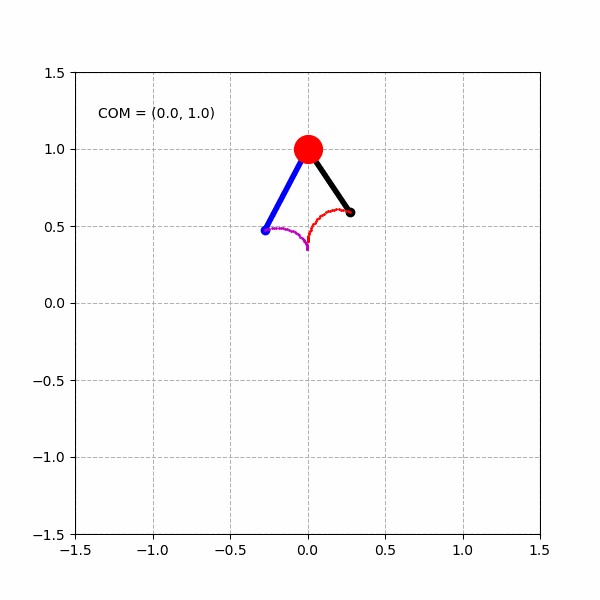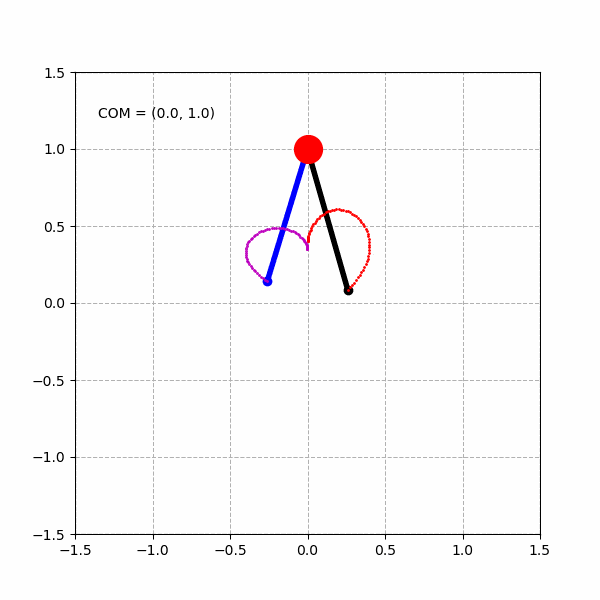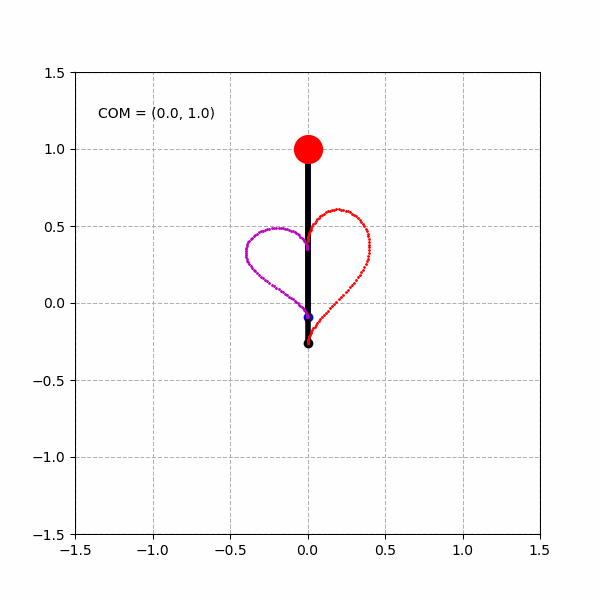
绘制3个不同的心形曲线:
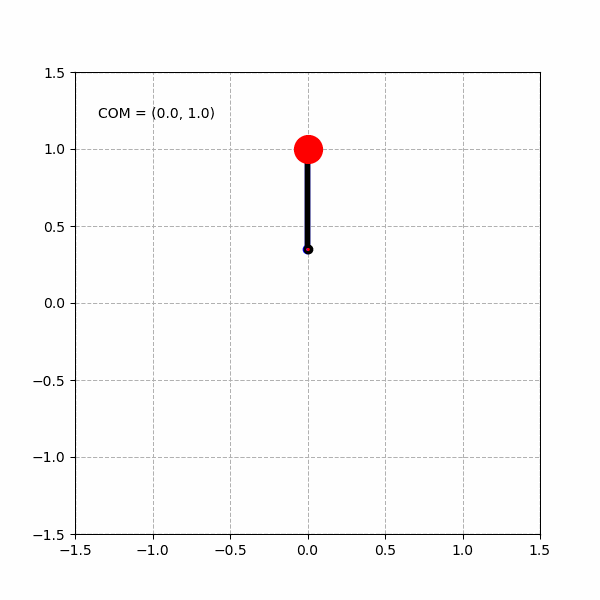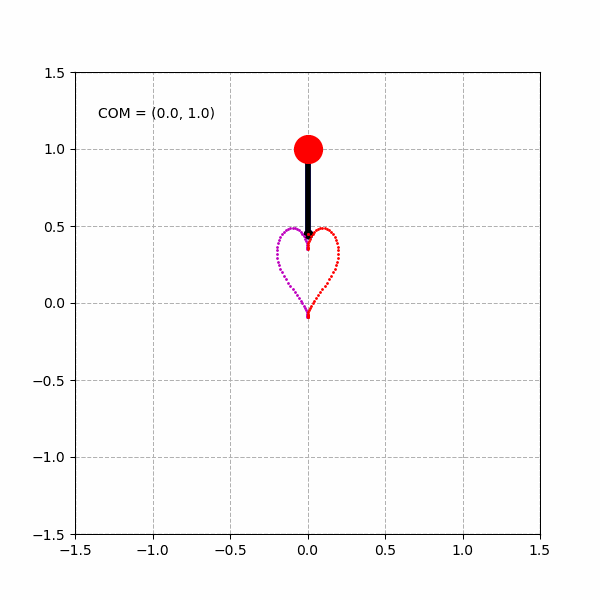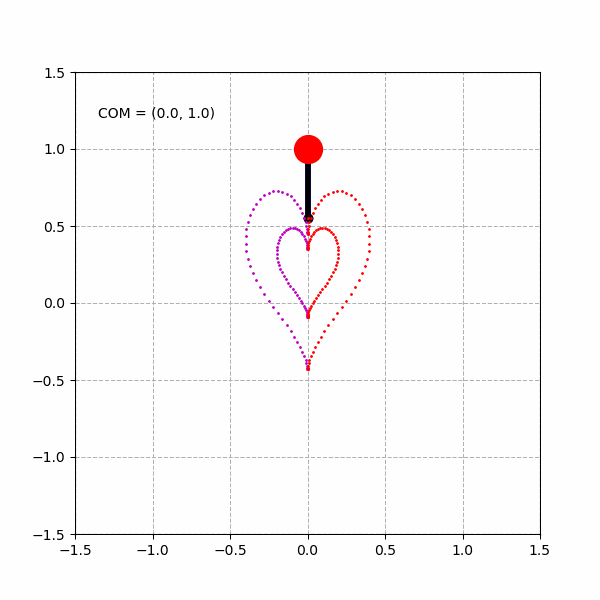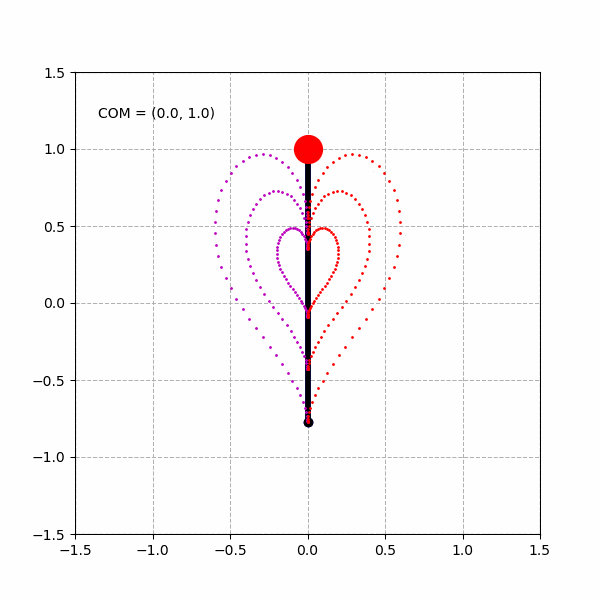
将心形曲线水平放缩:
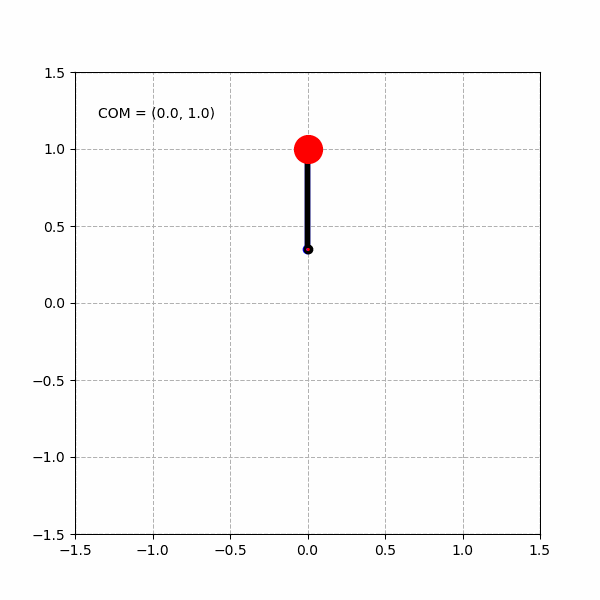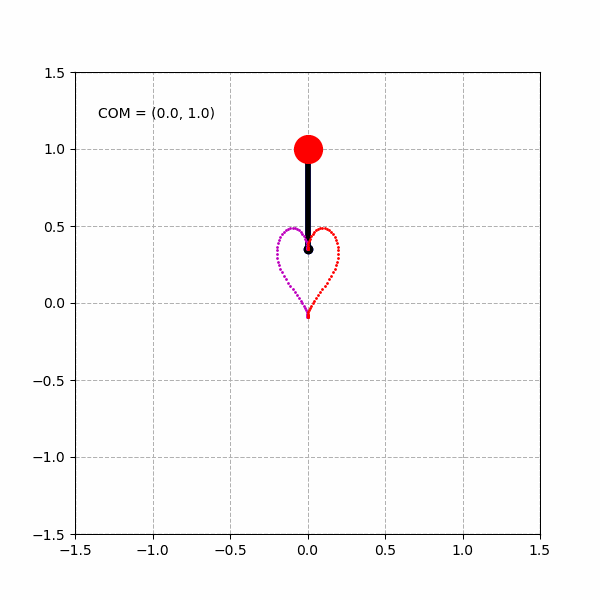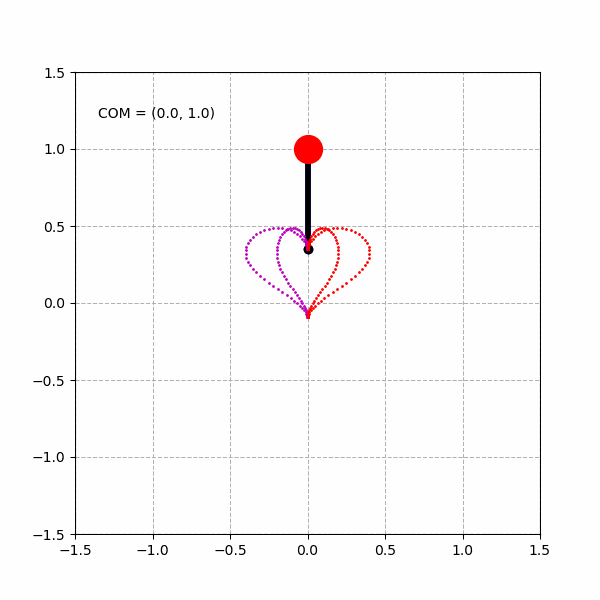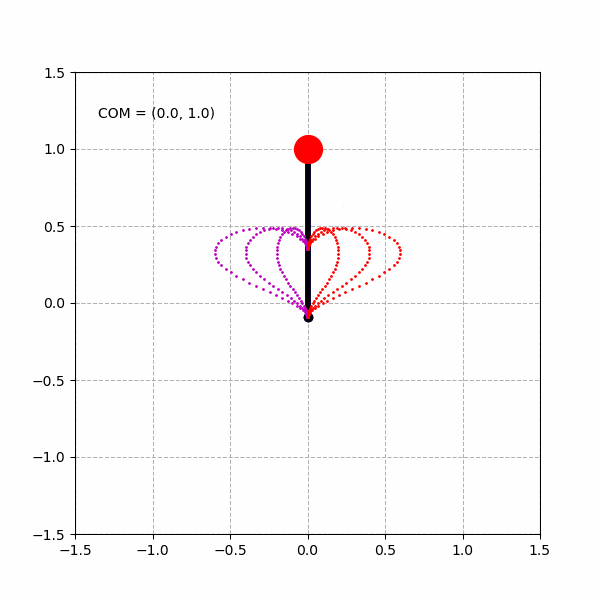
绘制多重的心形曲线:
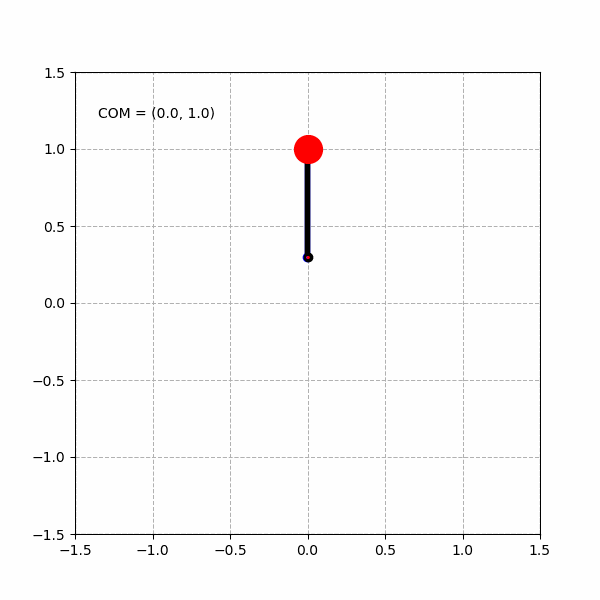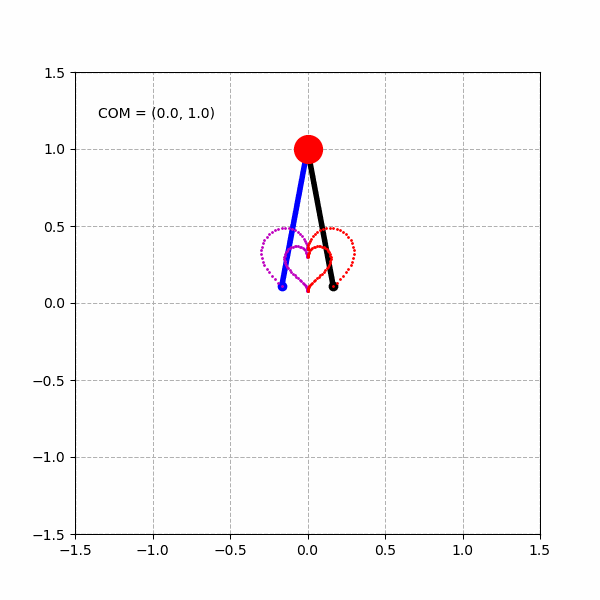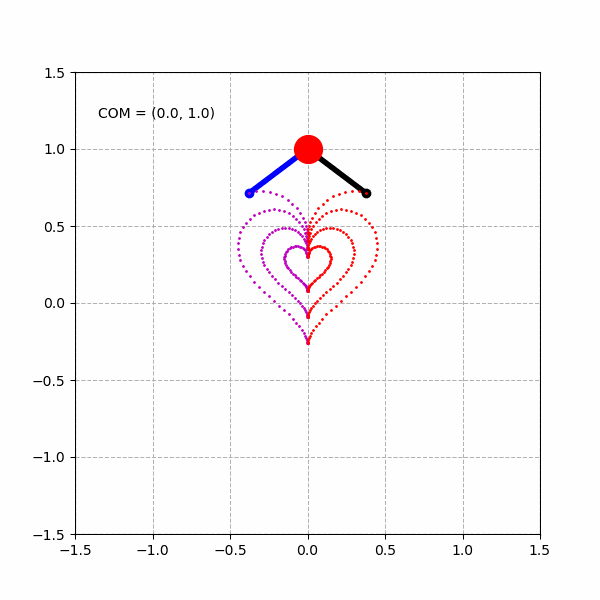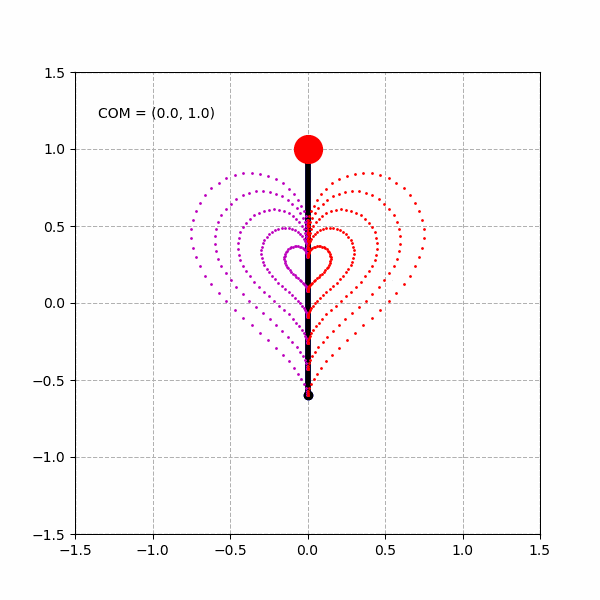
当然,由于实际的倒立摆模型的关节的运动范围是有限的,例如,我们将倒立摆模型的髋关节运动范围限制在 ,将膝关节运动范围限制在 ,则我们能得到类似下面变形了的“心形”图形。
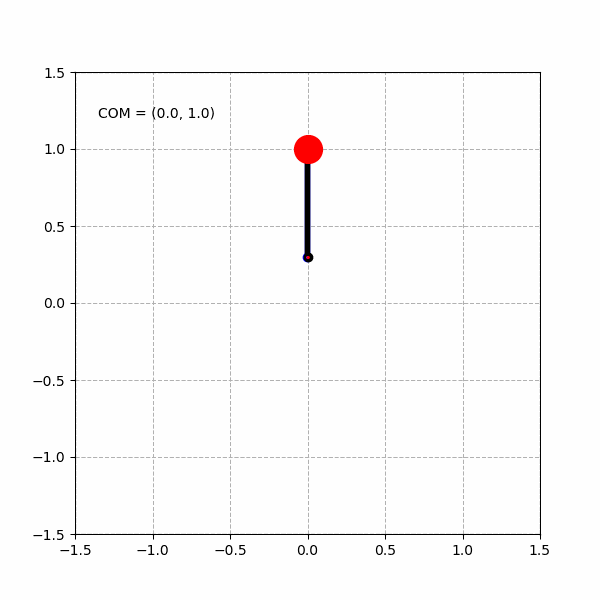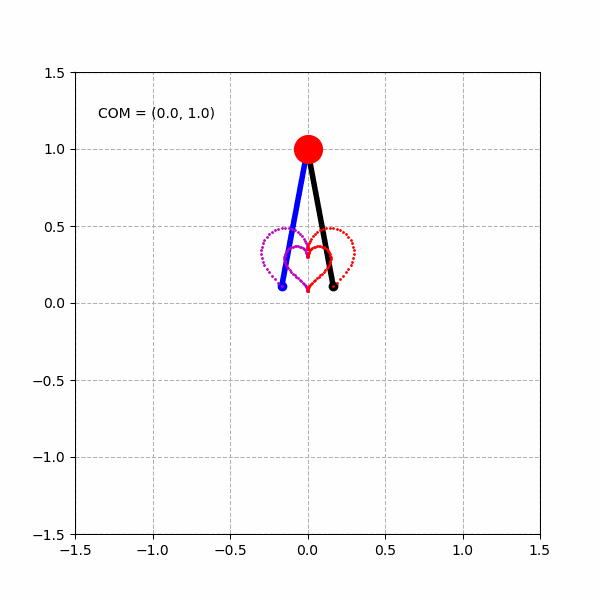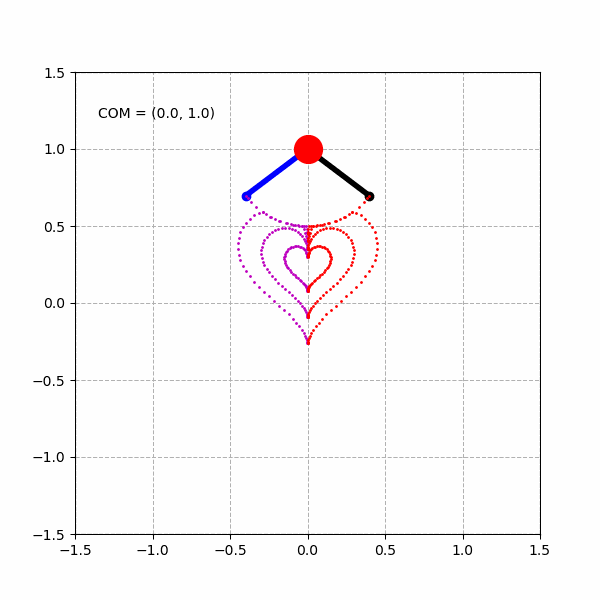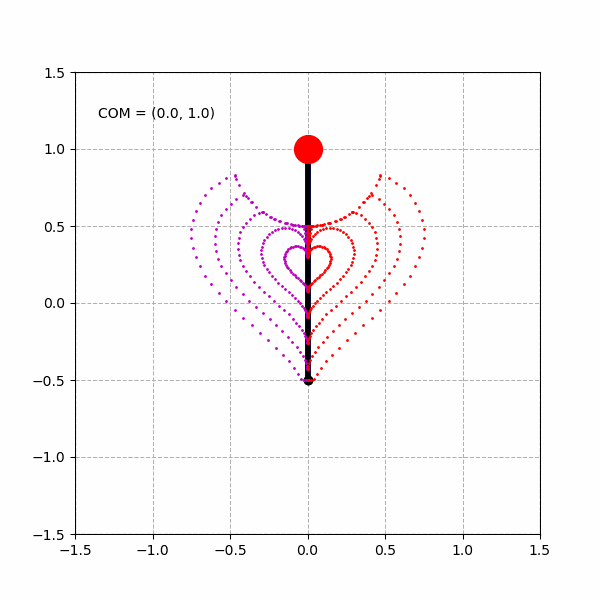
我们也可以将同样的逆运动学模型直接应用到VREP中,控制在VREP中的倒立摆仿真模型完成类似的工作:

4. 代码仓库
代码已在Github开源:https://github.com/chauby/BipedalWalkingRobots.git
5. 参考文献
Shuuji Kajita, Hirohisa Hirukawa et al. Introduction to Humanoid Robots, 2004. (中文译名《仿人机器人》——梶田秀司著)
公众号后台回复【HR】可获取书籍《仿人机器人》的下载链接。
























 355
355

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










