浅谈二叉树的四种遍历

一、先序遍历

       （1）定义

       （2）算法描述

二、中序遍历

       （1）定义

       （2）算法描述

三、后序遍历

       （1）定义

       （2）算法描述

四、层次遍历

       （1）定义

       （2）算法描述

一、先序遍历

 （1）定义：

    先序遍历二叉树的操作定义是:若二叉树为空，则空操作。否则，先访问根结点，其次先序遍历左子树，最后遍历右子树。

记忆口诀：先根，再左，再右

辅助记忆：先序遍历可以想象为，一个小人从一棵二叉树根节点为起点，沿着二叉树外沿，逆时针走一圈回到根节点，路上遇到的元素顺序，就是先序遍历的结果

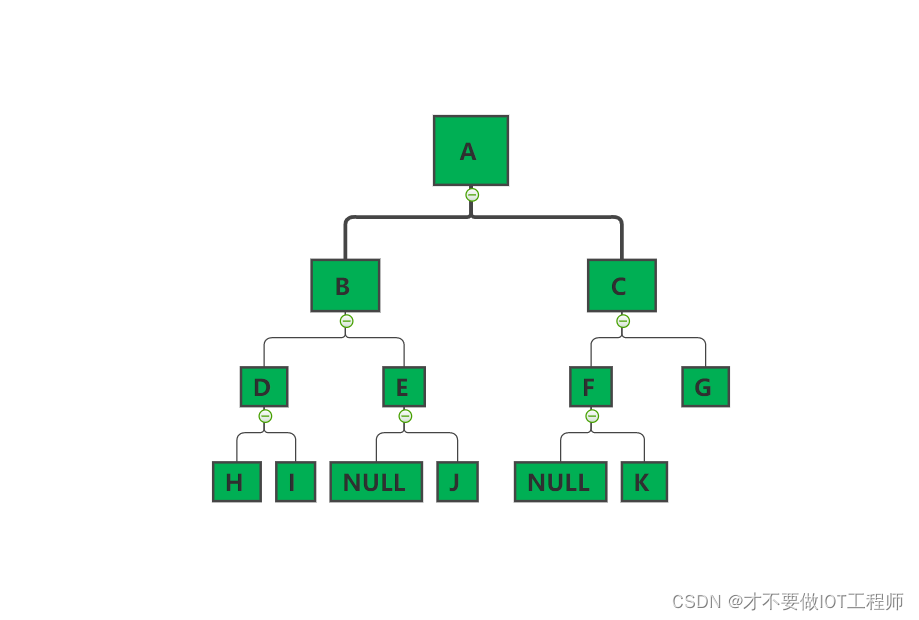
先序遍历结果：A B D H I E J C F K G

（2）算法描述

void CreateBiTree(BiTree& T)
{
	//按先序次序输入二叉树中的结点值，创建二叉链表表示的二叉树T
	cin >> ch;
	if (ch == '#')   //建立空树
		T = NULL;    //建立二叉树
	else
	{ 
	   	T = new BiTNode;   //生成根结点
		T->data = ch;      //根结点数据域置为ch
		CreateBiTree(T->1child); //创建左子树
		CreateBiTree(T->rchild);//创建右子树
	}
}

二、中序遍历

 （1）定义：

   中序遍历二叉树的操作定义是:若二叉树为空，则空操作。否则，先中序遍历左子树，其次访问根结点，最后遍历右子树。

记忆口诀：先左，再根，再右

辅助记忆：中序遍历可以看成，二叉树每个节点，垂直方向投影下来（可以理解为每个节点从最左边开始垂直掉到地上），然后从左往右数，得出的结果便是中序遍历的结果。

中遍历结果为：H D I B E J A F K C G 

（2）算法描述

void CreateBiTree(BiTree& T)
{
	//中序遍历二叉树T的递归算法
	if (T)                //若二叉树非空
	{
		InOrderTraverse(T->1child);//中序遍历左子树
		cout << T->data;           //访问根结点
		InOrderTraverse(T->rchild);//中序遍历右子树
	}
}

三、后序遍历

 （1）定义：

    后序遍历二叉树的操作定义是:若二叉树为空，则空操作。否则，先后序遍历左子树，其次遍历右子树，最后访问根结点。

记忆口诀：先左，再右，再根

辅助记忆：在后序遍历中，根节点默认最后面，其次可以看成在二叉树的每个结点，先把最左边的放在第一位，然后是右边，最后是中间，这样依次从左-右-根摆放就ok了。切记，最顶端的根结点默认放在最后面

后序遍历结果：H I D J E B K F G C A

 （2）算法描述

void CreateBiTree(BitTree & T)
{//		后序遍历二叉树T的算法
	if (T == NULL)						//	递归中遇到NULL，返回上一层节点
	{
		postorder traversal(T->lchild);			//	递归遍历左子树
		postorder traversal(T->rchild);			//	递归遍历右子树
}

四、层次遍历

 （1）定义：

     层次遍历就是从根节点开始，一层一层，从上到下，每层从左到右，依次写值就可以了

层次遍历结果：A B C D E F G H I J K

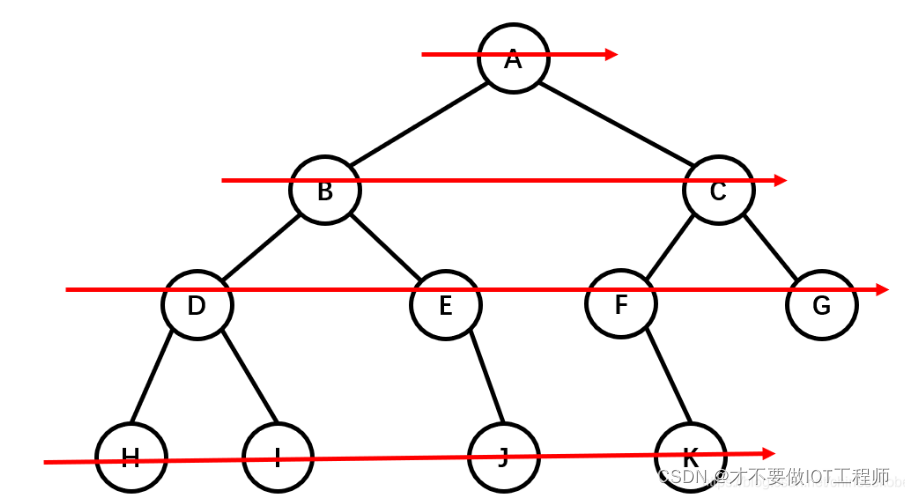
 （2）算法描述

void levelPrint(Tree* p) {
	//初始化一个非循环队列
	Treep stack[maxSize];
	int front, real;
	front = real = 0;
	Tree* curr, * pre;
	pre = p;
	while (pre != NULL) {
		// 输出当前节点的值 
		cout << pre->data;
		// 拿到当前节点的左孩子指针 
		curr = pre->lchild;
		//如果左孩子不为空 入队！
		if (curr != NULL) {
			stack[real++] = curr;
		}
		// 如果右孩子不为空 入队！ 
		curr = pre->rchild;
		if (curr != NULL) {
			stack[real++] = curr;

		}
		// 如果队列不为空则从队列取出元素 
		if (front != real)
			pre = stack[front++];
		else //否则直接置空指针 
			pre = NULL;

	}
}