1. 密码学介绍
我们上一次学习有关密码学的知识是在CAN201计算机网络中,这也是密码学常见的用途——保证通信安全。
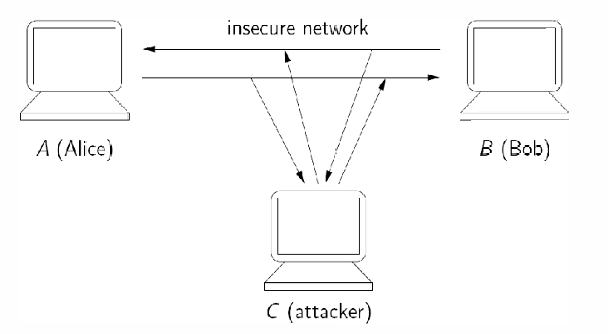
为此我们密码学需要实现以下这些目标:
- 数据完整性(Data Integrity)
含义:信息不应在未被检测的情况下被篡改。
解释:确保数据在存储、传输和处理过程中保持完整,没有被非法修改或损坏。例如,银行账户余额数据不能被未经授权的人员修改。 - 身份认证(Authentication)
含义:参与通信的主体必须被识别。
解释:验证通信双方的身份,确保他们是谁声称的那个人。例如,登录系统时需要输入用户名和密码,系统通过这些信息来确认用户的身份。 - 授权(Authorization)
含义:对敏感信息进行操作的主体必须被授权执行这些操作。
解释:只有经过授权的用户或系统才能访问或修改敏感信息。例如,只有医生和护士可以查看病人的病历,其他未经授权的人员无法访问。 - 不可抵赖性(Nonrepudiation)
含义:如果受到合同约束,主体不能在未被检测的情况下逃避其义务。
解释:确保通信双方不能否认他们已经执行的操作或做出的承诺。例如,一旦发送了电子邮件,发送者不能否认他们发送了这封邮件。 - 保密性(Confidentiality)
含义:敏感信息必须对未经授权访问的主体保密。
解释:确保只有授权的用户能够访问敏感信息,防止信息泄露。例如,公司的商业机密只能由特定的员工访问,其他人无法获取。
所以为了保护敏感信息,我们有对应的算法和技术。许多这些技术使用了数论,例如流行的RSA(Rivest-Shamir-Adleman)方案。保护信息安全不仅仅是数论的问题!安全协议需要被证明是正确的,这需要使用形式化方法(这是计算机科学的另一个领域,这里不会详细讨论)。
所以接下来我们将学习基础的数论。
1.1 数学基础
1.1.1 整数算术
1.1.1.1 整数集
整数集,用符号
Z
Z
Z表示,包含所有整数(没有小数部分),从负无穷大到正无穷大。
在密码学中,我们对整数集上的三种二元运算感兴趣(+、-、×)。二元运算是指需要两个输入并产生一个输出的操作。
1.1.1.2 二元运算
我们现在思考逆运算。
加法的逆运算是减法:如果
a
+
b
=
c
,那么
c
−
b
=
a
a+b=c,那么 c−b=a
a+b=c,那么c−b=a。
减法的逆运算是加法:如果
a
−
b
=
c
,那么
c
+
b
=
a
a−b=c,那么 c+b=a
a−b=c,那么c+b=a。
乘法的逆运算是除法(在整数范围内,除法不总是有整数解,但在模运算中可以定义逆运算)
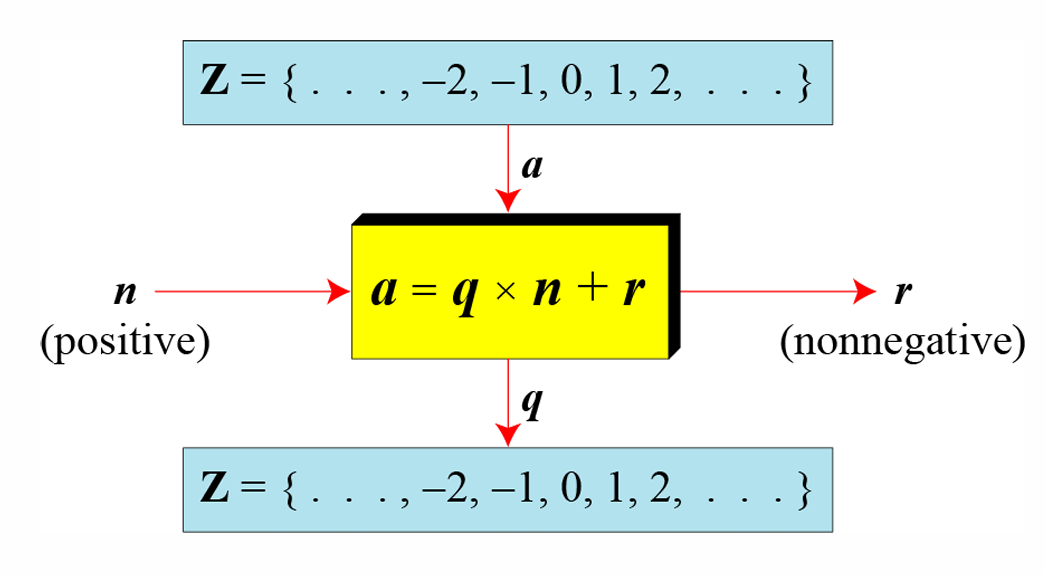
所以现在
a
=
q
×
n
+
r
a=q×n+r
a=q×n+r,即被除数
a
a
a可以表示为除数
n
n
n与商
q
q
q的乘积加上余数
r
r
r。余数的范围:
0
≤
r
<
∣
n
∣
0≤r<∣n∣
0≤r<∣n∣
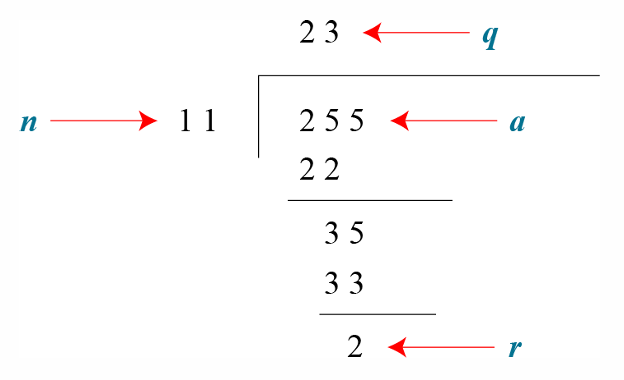
例子如下:假设
a
=
255
a=255
a=255和
n
=
11
n=11
n=11,通过除法算法,我们可以找到
q
=
23
q=23
q=23和
r
=
2
r=2
r=2。
1.1.1.3 整数除法
现在我们的算式如下。
当
a
a
a是负数时,直接进行除法运算可能会得到负的商
q
q
q和余数
r
r
r,这违反了余数必须是非负数的限制。
为了使余数
r
r
r为非负数,可以通过调整商
q
q
q来实现。具体方法是将商
q
q
q减
1
1
1,并将余数
r
r
r加上除数
n
n
n。这样,新的商和余数仍然满足原始等式
a
=
q
×
n
+
r
a=q×n+r
a=q×n+r,但余数
r
r
r变为非负数。
示例如下:假设
a
=
−
255
a=−255
a=−255和
n
=
11
n=11
n=11,直接计算得到的商和余数为:
−
255
=
(
−
23
×
11
)
+
(
−
2
)
−255=(−23×11)+(−2)
−255=(−23×11)+(−2)
这里,商
q
=
−
23
q=−23
q=−23和余数
r
=
−
2
r=−2
r=−2都是负数。
为了使余数
r
r
r为非负数,我们可以将商
q
q
q减
1
1
1,并将余数
r
r
r加上除数
n
n
n:
−
255
=
(
−
24
×
11
)
+
9
−255=(−24×11)+9
−255=(−24×11)+9
这样,新的商
q
=
−
24
q=−24
q=−24和新的余数
r
=
9
r=9
r=9满足余数必须是非负数的限制。
1.1.1.4 整除性(Divisibility)
如果
a
a
a不是零,并且在除法关系中我们设
r
=
0
r=0
r=0,那么我们得到:
a
=
q
×
n
a=q×n
a=q×n
如果余数是零,我们用符号
n
∣
a
n∣a
n∣a表示 n 能整除
a
a
a。
如果余数不是零,我们用符号
n
∤
a
n∤a
n∤a表示 n 不能整除
a
a
a。
例子如下:
1.
32
=
8
×
4
32=8×4
32=8×4,所以
4
∣
32
4∣32
4∣32。
2.
42
=
5
×
8
+
2
42=5×8+2
42=5×8+2,所以
8
∤
32
8∤32
8∤32。
现在我们说一些性质。
1.如果
a
a
a能整除
1
1
1,则
a
=
±
1
a=±1
a=±1。
2.如果
b
b
b能整除
a
a
a且
a
a
a能整除
b
b
b,则
a
=
±
b
a=±b
a=±b。
3.如果
b
b
b能整除
a
a
a且
c
c
c能整除
b
b
b,则
c
c
c能整除
a
a
a。
4.如果
a
a
a能整除
b
b
b且
a
a
a能整除
c
c
c,则
a
a
a能整除
m
×
b
+
n
×
c
m×b+n×c
m×b+n×c,其中
m
m
m和
n
n
n是任意整数。
现在我们讨论公因数(Common divisors)
我们可以通过维恩图的形式直观地展示了两个整数的因数集合从而获得公因数的结果。

最大公约数(Greatest Common Divisor, GCD)是两个正整数共有的最大的能同时整除它们的整数。
计算最大公约数可以使用欧几里得算法(Euclidean Algorithm)。
它利用了一个事实:
g
c
d
(
a
,
0
)
=
a
gcd(a,0)=a
gcd(a,0)=a,即如果两个数中的一个是
0
0
0,那么最大公约数就是另一个数。
因此我们获得了一个引理:设
a
,
b
,
q
a,b,q
a,b,q和
r
r
r是整数,满足
a
=
b
q
+
r
a=bq+r
a=bq+r且
b
≠
0
b≠0
b=0。则
g
c
d
(
a
,
b
)
=
g
c
d
(
b
,
r
)
gcd(a,b)=gcd(b,r)
gcd(a,b)=gcd(b,r)。
证明如下:设
d
=
g
c
d
(
a
,
b
)
d=gcd(a,b)
d=gcd(a,b)和
e
=
g
c
d
(
b
,
r
)
e=gcd(b,r)
e=gcd(b,r)。我们需要证明
d
=
e
d=e
d=e。
由于
d
d
d能整除
a
a
a和
b
b
b,所以
d
d
d也能整除
a
−
b
q
=
r
a−bq=r
a−bq=r。
因此,
d
d
d是
b
b
b和
r
r
r的公因数,所以
d
≤
e
d≤e
d≤e。
同样,由于
e
e
e能整除
b
b
b和
r
r
r,所以
e
e
e也能整除
b
q
+
r
=
a
bq+r=a
bq+r=a。
因此,
e
e
e是
a
a
a和
b
b
b的公因数,所以
e
≤
d
e≤d
e≤d。
这证明了
d
=
e
d=e
d=e。
当 g c d ( a , b ) = 1 gcd(a,b)=1 gcd(a,b)=1时,我们说 a a a和 b b b是互质的(relatively prime)。这意味着 a a a和 b b b没有除了 1 1 1以外的公因数。
所以欧几里得算法的步骤如下:
计算
a
a
a除以
b
b
b的商
q
q
q和余数
r
r
r,即
a
=
b
q
+
r
a=bq+r
a=bq+r。
如果
r
=
0
r=0
r=0,则
b
b
b就是最大公约数。
如果
r
≠
0
r≠0
r=0,则用
b
b
b和
r
r
r重复上述步骤,直到余数为
0
0
0。
最后一个非零余数就是最大公约数。
算法伪代码如下。

例子如下:
a
=
60
,
b
=
25
a= 60, b=25
a=60,b=25,所以
q
=
2
,
r
=
10
q=2,r=10
q=2,r=10。
a
=
25
,
b
=
10
a= 25, b=10
a=25,b=10,所以
q
=
2
,
r
=
5
q=2,r=5
q=2,r=5。
a
=
10
,
b
=
5
a= 10, b=5
a=10,b=5,所以
q
=
2
,
r
=
0
q=2,r=0
q=2,r=0。
a
=
5
,
b
=
0
a= 5, b=0
a=5,b=0,所以
g
c
d
(
25
,
60
)
=
5
gcd (25, 60) = 5
gcd(25,60)=5。
我们现在扩展欧几里得算法。
从而给定两个整数
a
a
a和
b
b
b,找到另外两个整数
s
s
s和
t
t
t,使得:
s
×
a
+
t
×
b
=
g
c
d
(
a
,
b
)
s×a+t×b=gcd(a,b)
s×a+t×b=gcd(a,b)。
在每一步的 GCD 计算中,余数
r
r
r可以表示为
a
−
b
q
a−bq
a−bq,而
g
c
d
(
a
,
b
)
gcd(a,b)
gcd(a,b)是最后一个有效的余数。
所以对于前面的例子我们有:
5
=
25
−
10
∗
2
=
25
−
(
60
−
25
∗
2
)
∗
2
=
5
∗
25
−
2
∗
60
5=25-10*2=25-(60-25*2)*2=5*25-2*60
5=25−10∗2=25−(60−25∗2)∗2=5∗25−2∗60
所以
s
=
−
2
,
t
=
5
s=-2,t=5
s=−2,t=5。
因此扩展欧几里得算法的步骤如下:
- 初始化:
r
1
←
a
;
r
2
←
b
r_1 ←a; r_2 ←b
r1←a;r2←b
s 1 ← 1 ; s 2 ← 0 s_1 ←1; s_2 ←0 s1←1;s2←0
t 1 ← 0 ; t 2 ← 1 t_1 ←0; t_2 ←1 t1←0;t2←1 - 当
r
2
>
0
r_2>0
r2>0时,执行以下步骤:
q ← r 1 / r 2 q←r_1/r_2 q←r1/r2
更新 r r r的值: r ← r 1 − q × r 2 ; r 1 ← r 2 ; r 2 ← r r←r_1-q×r_2;r_1←r_2;r_2←r r←r1−q×r2;r1←r2;r2←r
更新 s s s的值: s ← s 1 − q × s 2 ; s 1 ← s 2 ; s 2 ← s s←s_1-q×s_2;s_1←s_2;s_2←s s←s1−q×s2;s1←s2;s2←s
更新 t t t的值: t ← t 1 − q × t 2 ; t 1 ← t 2 ; t 2 ← t t←t_1-q×t_2;t_1←t_2;t_2←t t←t1−q×t2;t1←t2;t2←t - 输出:
g
c
d
(
a
,
b
)
←
r
1
;
s
←
s
1
;
t
←
t
1
gcd(a,b)←r_1;s←s_1;t←t_1
gcd(a,b)←r1;s←s1;t←t1

解释如下:
-
r
1
=
s
1
×
a
+
t
1
×
b
r_1=s_1×a+t_1×b
r1=s1×a+t1×b
r 2 = s 2 × a + t 2 × b r_2=s_2×a+t_2×b r2=s2×a+t2×b - 计算新的余数: r n e w = r 1 − q × r 2 = s 1 × a + t 1 × b − q ( s 2 × a + t 2 × b ) = ( s 1 − q × s 2 ) × a + ( t 1 − q × t 2 ) × b r_{new}=r_1-q×r_2=s_1×a+t_1×b-q(s_2×a+t_2×b)=(s_1-q×s_2)×a+(t_1-q×t_2)×b rnew=r1−q×r2=s1×a+t1×b−q(s2×a+t2×b)=(s1−q×s2)×a+(t1−q×t2)×b
- 新的余数 r n e w r_{new} rnew保持形式 r = r = s × a + t × b r= r=s×a+t×b r=r=s×a+t×b
- 系数更新为 s n e w = s 1 − q × s 2 s_{new}=s_1-q×s_2 snew=s1−q×s2, t n e w = t 1 − q × t 2 t_{new}=t_1-q×t_2 tnew=t1−q×t2
例子如下:
例1:
a
=
161
,
b
=
28
a = 161,b = 28
a=161,b=28。
先初始化。
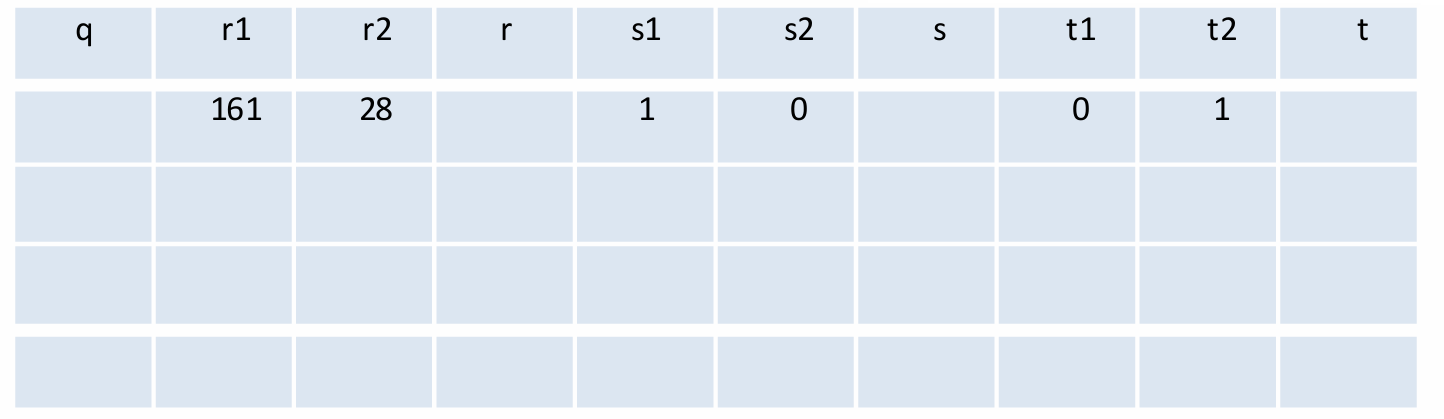
然后循环更新表格内的值。
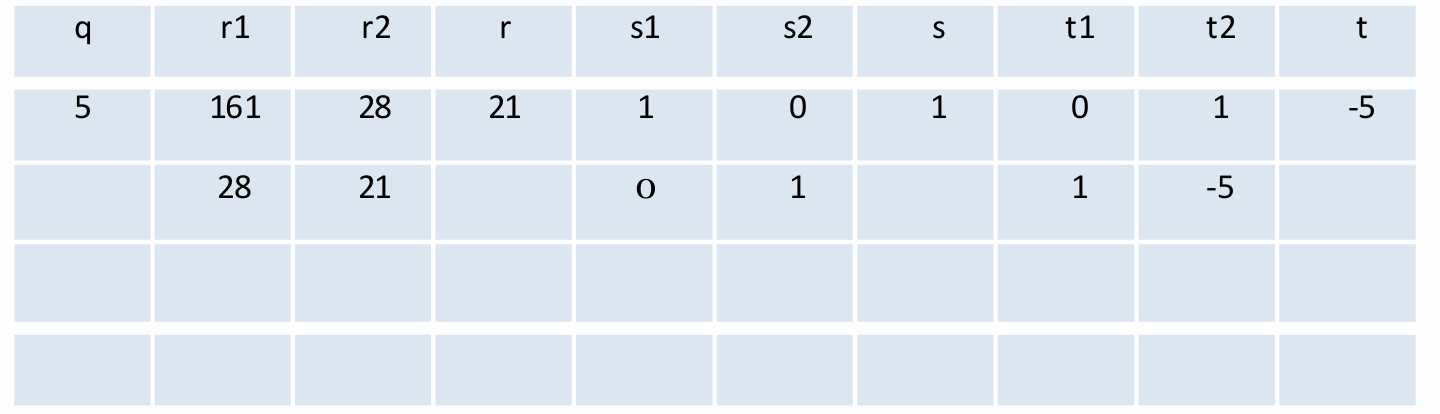
最后的结果如下。
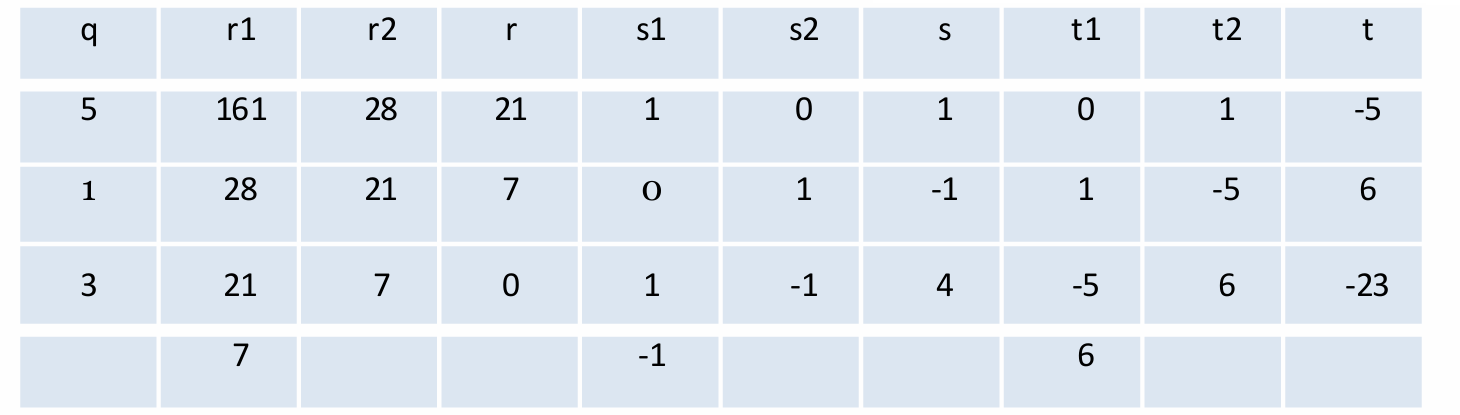
所以
g
c
d
(
161
,
28
)
=
7
,
s
=
−
1
,
t
=
6
gcd(161, 28) = 7, s = -1, t = 6
gcd(161,28)=7,s=−1,t=6。
例2:
a
=
391
,
b
=
299
a = 391,b = 299
a=391,b=299。
结果如下。

因此
g
c
d
(
391
,
299
)
=
23
,
s
=
−
3
,
t
=
4
gcd (391, 299) = 23, s = -3, t = 4
gcd(391,299)=23,s=−3,t=4。
1.1.2 模运算(Modular Arithmetic)
1.1.2.1 模运算符号
之前讨论的除法关系是
a
=
q
×
n
+
r
a=q×n+r
a=q×n+r,其中
a
a
a是被除数,
n
n
n 是除数,
q
q
q是商(quotient),
r
r
r是余数(remainder)。
在模运算中,我们只关心除法关系中的余数
r
r
r。
模运算符通常表示为 mod(在某些编程语言中可能表示为 %)。
模运算中的第二个输入(在除法关系
a
=
q
×
n
+
r
a=q×n+r
a=q×n+r中是
n
n
n)被称为模数(Modulus)。
模运算的输出
r
r
r被称为余数(residue)。
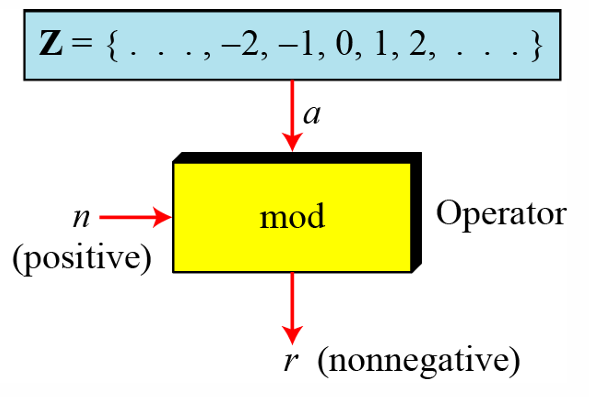
1.1.2.2 余数集
在模运算中,集合
Z
n
Z_n
Zn表示所有可能的余数,它由所有从
0
0
0到
n
−
1
n−1
n−1的整数组成。
表示为
Z
n
=
{
0
,
1
,
2
,
3
,
…
,
(
n
−
1
)
}
Z_n=\{0,1,2,3,…,(n−1)\}
Zn={0,1,2,3,…,(n−1)}。
例子如下:
Z
2
=
{
0
,
1
}
Z_2=\{0,1\}
Z2={0,1}
Z
6
=
{
0
,
1
,
2
,
3
,
4
,
5
}
Z_6=\{0,1,2,3,4,5\}
Z6={0,1,2,3,4,5}
Z
11
=
{
0
,
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
,
10
}
Z_{11}=\{0,1,2,3,4,5,6,7,8,9,10\}
Z11={0,1,2,3,4,5,6,7,8,9,10}
对于任何整数
a
a
a,模
n
n
n运算的结果是
a
a
a除以
n
n
n后的余数,表示为
a
m
o
d
n
a \ mod \ n
a mod n。
这个余数总是落在
0
0
0到
n
−
1
n−1
n−1的范围内,因此
Z
n
Z_n
Zn包含了所有可能的余数。
1.1.2.3 同余(Congruence)
在模运算中,如果两个整数
a
a
a和
b
b
b除以
m
m
m后余数相同,那么我们称
a
a
a和
b
b
b同余模
m
m
m。
这可以表示为
a
≡
b
(
m
o
d
m
)
a≡b(mod \ m)
a≡b(mod m)。
例子如下:
2
≡
12
(
m
o
d
10
)
2≡12(mod \ 10)
2≡12(mod 10):
2
2
2和
12
12
12除以
10
10
10后余数都是
2
2
2。
13
≡
23
(
m
o
d
10
)
13≡23(mod \ 10)
13≡23(mod 10):
13
13
13和
23
23
23除以
10
10
10后余数都是
3
3
3。
3
≡
8
(
m
o
d
5
)
3≡8(mod \ 5)
3≡8(mod 5):
3
3
3和
8
8
8除以
5
5
5后余数都是
3
3
3。
8
≡
13
(
m
o
d
5
)
8≡13(mod \ 5)
8≡13(mod 5):
8
8
8和
13
13
13除以
5
5
5后余数都是
3
3
3。
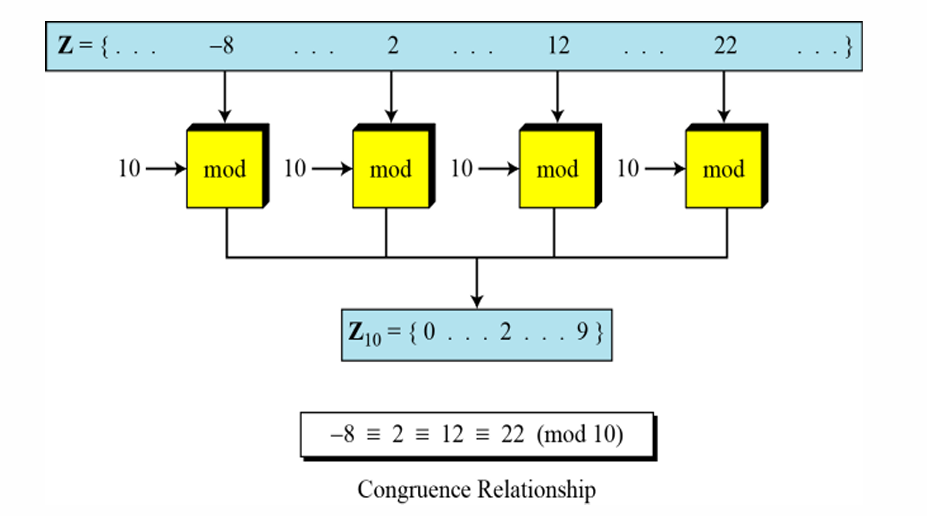
同余类
[
a
]
[a]
[a]或
[
a
]
n
[a]_n
[a]n是指所有与
a
a
a模
n
n
n同余的整数的集合。
形式上,这个集合可以表示为
{
…
,
a
−
3
n
,
a
−
2
n
,
a
−
n
,
a
,
a
+
n
,
a
+
2
n
,
a
+
3
n
,
…
}
\{…,a−3n,a−2n,a−n,a,a+n,a+2n,a+3n,…\}
{…,a−3n,a−2n,a−n,a,a+n,a+2n,a+3n,…}。
例如
n
=
5
n=5
n=5时,有以下同余类。
[
0
]
=
{
…
,
−
15
,
−
10
,
−
5
,
0
,
5
,
10
,
15
,
…
}
[0]=\{…,−15,−10,−5,0,5,10,15,…\}
[0]={…,−15,−10,−5,0,5,10,15,…}
[
1
]
=
{
…
,
−
14
,
−
9
,
−
4
,
1
,
6
,
11
,
16
,
…
}
[1]=\{…,−14,−9,−4,1,6,11,16,…\}
[1]={…,−14,−9,−4,1,6,11,16,…}
[
2
]
=
{
…
,
−
13
,
−
8
,
−
3
,
2
,
7
,
12
,
17
,
…
}
[2]=\{…,−13,−8,−3,2,7,12,17,…\}
[2]={…,−13,−8,−3,2,7,12,17,…}
[
3
]
=
{
…
,
−
12
,
−
7
,
−
5
,
3
,
8
,
13
,
18
,
…
}
[3]=\{…,−12,−7,−5,3,8,13,18,…\}
[3]={…,−12,−7,−5,3,8,13,18,…}
[
4
]
=
{
…
,
−
11
,
−
6
,
−
1
,
4
,
9
,
14
,
19
,
…
}
[4]=\{…,−11,−6,−1,4,9,14,19,…\}
[4]={…,−11,−6,−1,4,9,14,19,…}
1.1.2.4 二元运算
之前讨论的整数集
Z
Z
Z上的三种二元运算(加法、减法和乘法)也可以在模
n
n
n剩余类集合
Z
n
Z_n
Zn上定义。
对于
Z
n
Z_n
Zn中的两个元素
a
a
a和
b
b
b,它们的和
a
+
b
a+b
a+b可能不在
Z
n
Z_n
Zn中(即结果可能大于或等于
n
n
n)。
为了将结果映射回
Z
n
Z_n
Zn,需要计算
(
a
+
b
)
m
o
d
n
(a+b) \ mod \ n
(a+b) mod n。
类似地,
a
−
b
a−b
a−b的结果也可能不在
Z
n
Z_n
Zn中。
需要计算
(
a
−
b
)
m
o
d
n
(a-b) \ mod \ n
(a−b) mod n来得到
Z
n
Z_n
Zn中的结果。
同理计算
(
a
×
b
)
m
o
d
n
(a×b) \ mod \ n
(a×b) mod n来得到
Z
n
Z_n
Zn中的结果。
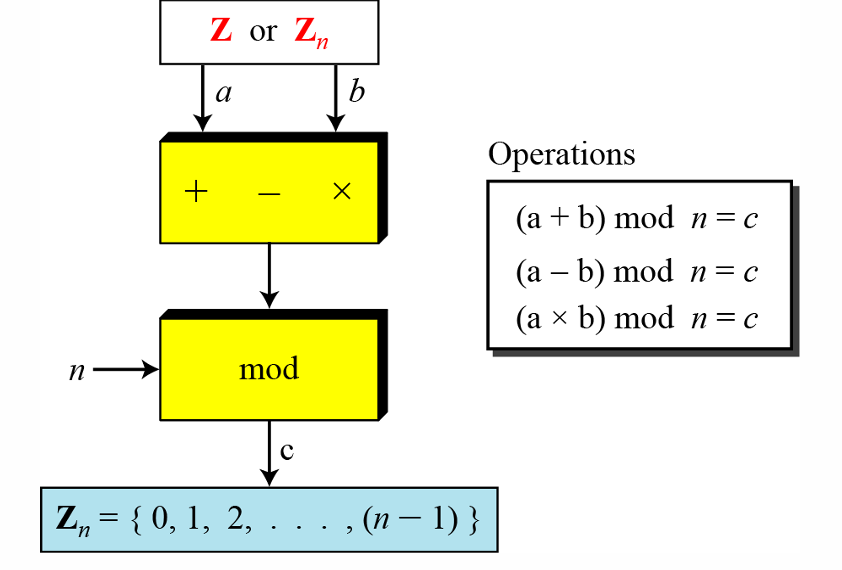
我们说一下这里的一些性质:
- ( a + b ) m o d n = [ ( a m o d n ) + ( b m o d n ) ] m o d n (a+b) \ mod \ n=[(a \ mod \ n)+(b \ mod \ n)] \ mod \ n (a+b) mod n=[(a mod n)+(b mod n)] mod n
- ( a − b ) m o d n = [ ( a m o d n ) − ( b m o d n ) ] m o d n (a-b) \ mod \ n=[(a \ mod \ n)-(b \ mod \ n)] \ mod \ n (a−b) mod n=[(a mod n)−(b mod n)] mod n
- ( a × b ) m o d n = [ ( a m o d n ) × ( b m o d n ) ] m o d n (a×b) \ mod \ n=[(a \ mod \ n)×(b \ mod \ n)] \ mod \ n (a×b) mod n=[(a mod n)×(b mod n)] mod n
例子如下:
计算
(
37
+
99
)
m
o
d
6
(37+99) \ mod \ 6
(37+99) mod 6:
直接计算:
37
+
99
=
136
37+99=136
37+99=136,然后
136
m
o
d
6
=
4
136 \ mod \ 6=4
136 mod 6=4。
使用性质:
[
(
37
m
o
d
6
)
+
(
99
m
o
d
6
)
]
m
o
d
6
=
(
1
+
3
)
m
o
d
6
=
4
[(37 \ mod \ 6)+(99 \ mod \ 6)] \ mod \ 6=(1+3)\ mod \ 6=4
[(37 mod 6)+(99 mod 6)] mod 6=(1+3) mod 6=4。
再比如我们计算
10
10
10的幂次除以某个整数时的余数,
10
n
m
o
d
x
10^n \ mod \ x
10n mod x,其中
x
x
x是任意整数。
我们可以利用模运算的第三性质,可以将
10
n
m
o
d
x
10^n \ mod \ x
10n mod x转化为
(
10
m
o
d
x
)
n
m
o
d
x
(10 \ mod \ x) ^n \ mod \ x
(10 mod x)n mod x。
所以
10
n
m
o
d
3
=
(
10
m
o
d
3
)
n
m
o
d
3
=
1
10^n \ mod \ 3 = (10 \ mod \ 3)^n \ mod \ 3 =1
10n mod 3=(10 mod 3)n mod 3=1。
10
n
m
o
d
9
=
(
10
m
o
d
9
)
n
m
o
d
9
=
1
10^n \ mod \ 9 = (10 \ mod \ 9)^n \ mod \ 9 =1
10n mod 9=(10 mod 9)n mod 9=1。
10
n
m
o
d
7
=
(
10
m
o
d
7
)
n
m
o
d
7
=
3
n
m
o
d
7
10^n \ mod \ 7 = (10 \ mod \ 7)^n \ mod \ 7 =3^n \ mod \ 7
10n mod 7=(10 mod 7)n mod 7=3n mod 7。
因此我们以前知道一个整数除以
3
3
3的余数与它的各位数字之和除以
3
3
3的余数相同(一个数是
3
3
3的倍数如果它的各位数字之和是
3
3
3的倍数)的原理如下:
a
=
a
n
×
10
n
+
.
.
.
+
a
1
×
10
1
+
a
0
×
10
0
a=a_n×10^n+...+a_1×10^1+a_0×10^0
a=an×10n+...+a1×101+a0×100。
例如,6371就可以表示为
6
×
10
3
+
.
.
.
+
3
×
10
2
+
7
×
10
1
+
1
×
10
0
6×10^3+...+3×10^2+7×10^1+1×10^0
6×103+...+3×102+7×101+1×100。
根据前面的性质2和性质3我们就可以化简得到
a
m
o
d
3
=
(
a
n
×
10
n
+
.
.
.
+
a
1
×
10
1
+
a
0
×
10
0
)
m
o
d
3
=
[
(
a
n
×
10
n
)
m
o
d
3
+
.
.
.
+
(
a
1
×
10
1
)
m
o
d
3
+
(
a
0
×
10
0
)
m
o
d
3
]
m
o
d
3
=
[
(
a
n
m
o
d
3
)
×
(
10
n
m
o
d
3
)
+
.
.
.
+
(
a
1
m
o
d
3
)
×
(
10
1
m
o
d
3
)
+
(
a
n
m
o
d
3
)
×
(
10
0
m
o
d
3
)
]
m
o
d
3
=
[
a
n
m
o
d
3
+
.
.
.
+
a
1
m
o
d
3
+
a
0
m
o
d
3
]
m
o
d
3
=
(
a
n
+
.
.
.
+
a
1
+
a
0
)
m
o
d
3
a \ mod \ 3 =(a_n×10^n+...+a_1×10^1+a_0×10^0) \ mod \ 3 = [(a_n×10^n) \ mod \ 3+...+(a_1×10^1) \ mod \ 3+(a_0×10^0) \ mod \ 3] \ mod \ 3 = [(a_n \ mod \ 3) ×(10^n \ mod \ 3) +...+(a_1 \ mod \ 3) ×(10^1 \ mod \ 3) +(a_n \ mod \ 3) ×(10^0 \ mod \ 3) ] \ mod \ 3 = [a_n \ mod 3 + ... + a_1 \ mod \ 3 + a_0 \ mod \ 3] \ mod \ 3 = (a_n + ... + a_1+a_0) \ mod \ 3
a mod 3=(an×10n+...+a1×101+a0×100) mod 3=[(an×10n) mod 3+...+(a1×101) mod 3+(a0×100) mod 3] mod 3=[(an mod 3)×(10n mod 3)+...+(a1 mod 3)×(101 mod 3)+(an mod 3)×(100 mod 3)] mod 3=[an mod3+...+a1 mod 3+a0 mod 3] mod 3=(an+...+a1+a0) mod 3 。
1.1.2.5 加法逆元(Additive Inverse)
在
Z
n
Z_n
Zn中,如果两个数
a
a
a和
b
b
b满足
a
+
b
≡
0
(
m
o
d
n
)
a+b≡0(mod \ n)
a+b≡0(mod n),那么
a
a
a和
b
b
b互为加法逆元。
在模运算中,每个整数都有一个加法逆元。
例子如下:假设
n
=
5
n=5
n=5,所以
Z
5
=
0
,
1
,
2
,
3
,
4
Z_5={0,1,2,3,4}
Z5=0,1,2,3,4
对于
a
=
1
a=1
a=1,它的加法逆元是
4
4
4,因为
1
+
4
=
5
1+4=5
1+4=5,而
5
m
o
d
5
=
0
5 \ mod \ 5=0
5 mod 5=0。
对于
a
=
2
a=2
a=2,它的加法逆元是
3
3
3,因为
2
+
3
=
5
2+3=5
2+3=5,而
5
m
o
d
5
=
0
5 \ mod \ 5=0
5 mod 5=0。
1.1.2.6 乘法逆元(Multiplicative Inverse)
在
Z
n
Z_n
Zn中,如果两个数
a
a
a和
b
b
b满足
a
×
b
≡
1
(
m
o
d
n
)
a×b≡1(mod \ n)
a×b≡1(mod n),那么
a
a
a和
b
b
b互为乘法逆元。
在模运算中,一个整数可能有也可能没有乘法逆元。
同样的例子下:
对于
a
=
1
a=1
a=1,它的乘法逆元是
1
1
1,因为
1
×
1
=
1
1×1=1
1×1=1,而
1
m
o
d
5
=
1
1 \ mod \ 5=1
1 mod 5=1。
对于
a
=
2
a=2
a=2,它的乘法逆元是
3
3
3,因为
2
×
3
=
6
2×3=6
2×3=6,而
6
m
o
d
5
=
1
6 \ mod \ 5=1
6 mod 5=1。
对于
a
=
4
a=4
a=4,它的乘法逆元是
4
4
4,因为
4
×
4
=
16
4×4=16
4×4=16,而
16
m
o
d
5
=
1
16 \ mod \ 5=1
16 mod 5=1。
扩展欧几里得算法可以用来找到
b
b
b在
Z
n
Z_n
Zn中的乘法逆元,前提是
n
n
n和
b
b
b互质,即
g
c
d
(
n
,
b
)
=
1
gcd(n,b)=1
gcd(n,b)=1。此外还会找到整数
s
s
s和
t
t
t使得
s
×
n
+
t
×
b
=
g
c
d
(
n
,
b
)
s×n+t×b=gcd(n,b)
s×n+t×b=gcd(n,b)。
由于
g
c
d
(
n
,
b
)
=
1
,我们有
s
×
n
+
t
×
b
=
1
gcd(n,b)=1,我们有 s×n+t×b=1
gcd(n,b)=1,我们有s×n+t×b=1。
在模
n
n
n的情况下,这意味着
t
×
b
≡
1
(
m
o
d
n
)
t×b≡1(mod \ n)
t×b≡1(mod n),因此
t
t
t就是
b
b
b在
Z
n
Z_n
Zn中的乘法逆元。
乘法逆元通常表示为
b
−
1
(
m
o
d
n
)
b^{−1} (mod \ n)
b−1(mod n)。

这里图片上是
t
1
t_1
t1因为前面扩展算法输出的
t
t
t是这里的
t
1
t_1
t1。
步骤如下:
- 初始化:
r
1
←
n
;
r
2
←
b
r_1←n;r_2←b
r1←n;r2←b,初始化两个余数。
t 1 ← 0 ; t 2 ← 1 t_1←0;t_2←1 t1←0;t2←1,初始化两个系数。 - 循环:当
r
2
>
0
r_2>0
r2>0时,执行以下步骤:
q ← r 1 / r 2 q←r_1/r_2 q←r1/r2。
r ← r 1 − q × r 2 r←r_1-q×r_2 r←r1−q×r2,更新余数 r r r。
r 1 ← r 2 ; r 2 ← r r_1←r_2;r_2←r r1←r2;r2←r,更新余数 r 1 r_1 r1和 r 2 r_2 r2。
t ← t 1 − q × t 2 t←t_1-q×t_2 t←t1−q×t2,更新余数 t t t。
t 1 ← t 2 ; t 2 ← t t_1←t_2;t_2←t t1←t2;t2←t,更新余数 t 1 t_1 t1和 t 2 t_2 t2。 - 如果 r 1 = 1 r_1=1 r1=1,则 t 1 t_1 t1就是 b b b在 Z n Z_n Zn中的乘法逆元,记作 b − 1 ← t 1 b ^{−1}←t _1 b−1←t1。
例子如下:找到
11
11
11在
Z
26
Z_{26}
Z26中的乘法逆元。
过程如下。
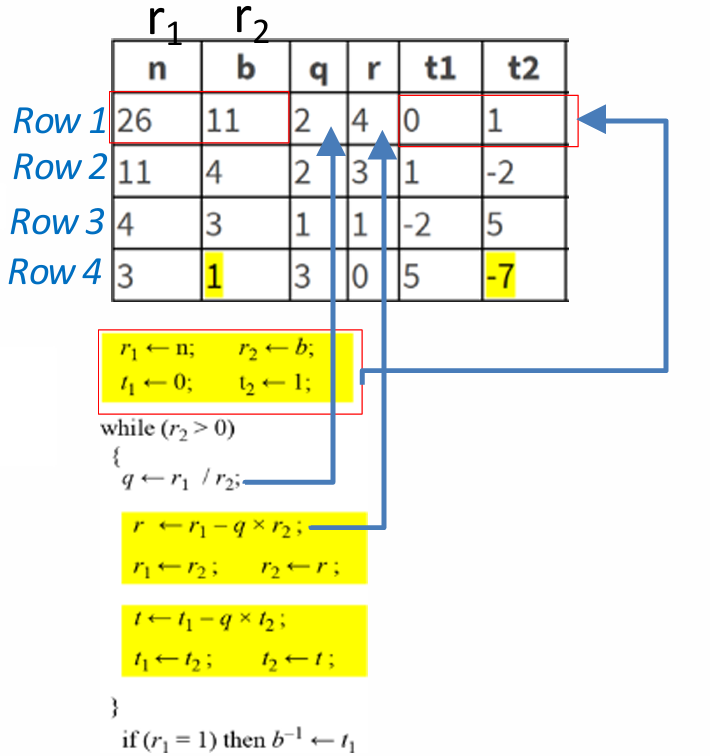
因此结果为 ( − 7 ) (-7) (−7),但是我们需要将其化成正乘法逆元,所以 ( − 7 ) m o d 26 = 19 (-7) \ mod \ 26 = 19 (−7) mod 26=19。
1.1.2.7 Different Sets
Z
n
Z_n
Zn是模
n
n
n的所有余数的集合,包含从
0
0
0到
n
−
1
n−1
n−1的所有整数。
Z
n
∗
Z_n^*
Zn∗是模
n
n
n的所有与
n
n
n互质的余数的集合,即
g
c
d
(
a
,
n
)
=
1
gcd(a,n)=1
gcd(a,n)=1的所有
a
a
a。
例如
Z
6
∗
=
{
1
,
5
}
,
Z
7
∗
=
{
1
,
2
,
3
,
4
,
5
,
6
}
,
Z
10
∗
=
{
1
,
3
,
7
,
9
}
Z_6^*=\{1,5\},Z_7^*=\{1,2,3,4,5,6\},Z_{10}^*=\{1,3,7,9\}
Z6∗={1,5},Z7∗={1,2,3,4,5,6},Z10∗={1,3,7,9}
当需要加法逆元时,使用
Z
n
Z_n
Zn集合。当需要乘法逆元时,使用
Z
n
∗
Z_n^*
Zn∗集合。
在密码学中,经常使用两个特殊的集合:
Z
p
Z_p
Zp和
Z
p
∗
Z_p^*
Zp∗,其中
p
p
p是一个素数。
例如
Z
13
=
{
0
,
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
,
10
,
11
,
12
}
,
Z
13
∗
=
{
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
,
10
,
11
,
12
}
Z_{13}=\{0,1,2,3,4,5,6,7,8,9,10,11,12\},Z_{13}^*=\{1,2,3,4,5,6,7,8,9,10,11,12\}
Z13={0,1,2,3,4,5,6,7,8,9,10,11,12},Z13∗={1,2,3,4,5,6,7,8,9,10,11,12}
1.1.3 线性同余
在密码学中经常出现一种形式为
a
x
≡
b
(
m
o
d
n
)
ax≡b(mod \ n)
ax≡b(mod n)的方程,其中
a
、
b
a、b
a、b和
n
n
n是给定的整数,而
x
x
x是需要找到的变量。也就是找到数
x
x
x和
q
q
q,使得
a
x
+
q
n
=
b
ax+qn=b
ax+qn=b。
该方程可能无解,也可能有解。
设
d
=
g
c
d
(
a
,
n
)
d=gcd(a,n)
d=gcd(a,n),即
a
a
a和
n
n
n的最大公约数。
如果
d
d
d不能整除
b
b
b(即
d
∤
b
d∤b
d∤b),则方程无解。
如果
d
d
d能整除
b
b
b(即
d
∣
b
d∣b
d∣b),则方程有解。
示例如下:
例1:
10
x
≡
2
(
m
o
d
15
)
10 x ≡ 2(mod \ 15)
10x≡2(mod 15)
首先
g
c
d
(
10
,
15
)
=
5
gcd(10,15)=5
gcd(10,15)=5,因为
5
5
5不能整除
2
2
2,所以无解。
例2:
7
x
≡
6
(
m
o
d
9
)
7 x ≡ 6 (mod \ 9)
7x≡6(mod 9)
因为
g
c
d
(
7
,
9
)
=
1
gcd(7,9)=1
gcd(7,9)=1,
1
∣
6
1|6
1∣6,所以有一个解。
现在我们需要找到
7
7
7在模
9
9
9下的乘法逆元。这意味着找到一个整数,使得
7
×
7
−
1
≡
1
(
m
o
d
9
)
7×7^ {−1}≡1(mod \ 9)
7×7−1≡1(mod 9)。
通过计算或使用扩展欧几里得算法,可以找到
7
−
1
≡
4
(
m
o
d
9
)
7^{−1}≡4(mod \ 9)
7−1≡4(mod 9)(因为
7
×
4
=
28
≡
1
(
m
o
d
9
)
7×4=28≡1(mod \ 9)
7×4=28≡1(mod 9))。
将原方程 7x≡6(mod9) 两边同时乘以
7
−
1
7^{−1}
7−1(即
4
4
4):
x
≡
(
6
×
4
)
(
m
o
d
9
)
≡
24
(
m
o
d
9
)
x≡(6×4)(mod \ 9)≡24(mod \ 9)
x≡(6×4)(mod 9)≡24(mod 9)
化简得到
x
=
6
x=6
x=6。
例3:
3
x
+
4
≡
6
(
m
o
d
13
)
3 x + 4 ≡ 6 (mod \ 13)
3x+4≡6(mod 13)
首先,将方程转换为
a
x
≡
b
(
m
o
d
n
)
ax≡b(mod \ n)
ax≡b(mod n)的形式,因此我们两边同时加
−
4
-4
−4,得到
3
x
≡
2
(
m
o
d
13
)
3x≡2(mod \ 13)
3x≡2(mod 13)。
因为
g
c
d
(
3
,
13
)
=
1
gcd(3,13)=1
gcd(3,13)=1,所以房产有唯一解。
现在找到
3
3
3在模
13
13
13下的乘法逆元。乘法逆元
3
−
1
3^{−1}
3−1满足
3
×
3
−
1
≡
1
(
m
o
d
13
)
3×3^{−1}≡1(mod \ 13)
3×3−1≡1(mod 13)。
通过计算或使用扩展欧几里得算法,可以找到
3
−
1
≡
9
(
m
o
d
13
)
3^{−1}≡9(mod\ 13)
3−1≡9(mod 13)(因为
3
×
9
=
27
≡
1
(
m
o
d
13
)
3×9=27≡1(mod \ 13)
3×9=27≡1(mod 13))。
因此
x
=
(
2
×
3
−
1
)
m
o
d
13
=
(
2
×
9
)
m
o
d
13
=
5
x=(2 × 3^{-1}) mod \ 13 = (2 × 9) \ mod \ 13 =5
x=(2×3−1)mod 13=(2×9) mod 13=5。
我们也可以验证一下
19
≡
6
(
m
o
d
13
)
19≡6(mod \ 13)
19≡6(mod 13),因此
x
=
5
x=5
x=5。
1.2 密码通信(Cryptographic communications)
在历史上,人们一直有需要(或希望)通过不安全的渠道安全地传输信息。
为了促进这种类型的通信,已经开发了多种密码学方法。这些方法包括:
加密/解密转换:加密是将信息转换为一种只有授权接收者才能理解的形式的过程。解密是将加密信息还原为原始形式的过程。
数字签名:数字签名是一种验证信息来源和完整性的方法。它确保信息是由声称的发送者发送的,并且在传输过程中未被篡改。
密码学在商业、军事、互联网上广泛应用。
1.2.1 加密方案(Encryption schemes)
加密方案或密码用于实现通信的保密性。
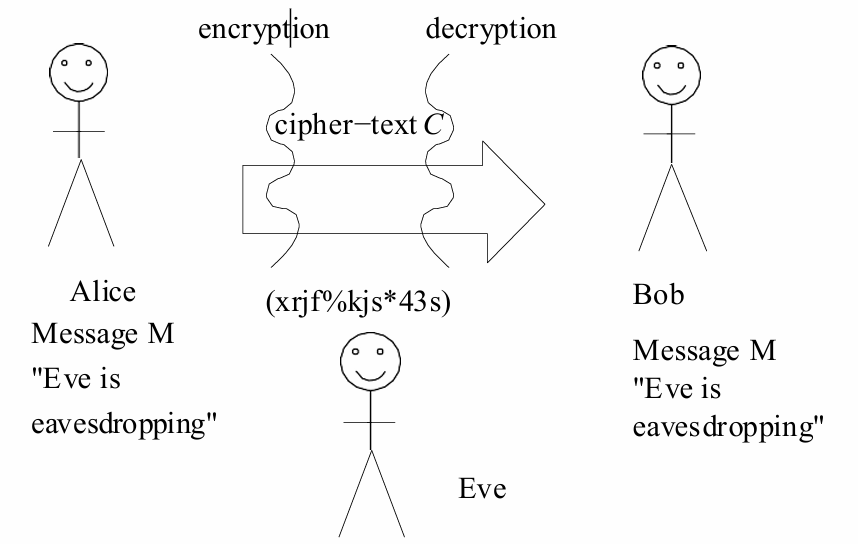
加密方案的基本原理是将待发送的消息
M
M
M(通常称为明文,plaintext)加密成一串无法识别的字符
C
C
C(称为密文,ciphertext)。
密文
C
C
C被传输给接收者,接收者解密
C
C
C以恢复原始消息
M
M
M。
这里的术语如下:
- 明文(M,plaintext):
原始消息,例如 “HELLO”。 - 密文(C,ciphertext):
加密后的字符串,例如 “KHOOOR”。 - 加密(Encryption):
将明文转换为密文的过程。 - 解密(Decryption):
将密文转换回明文的过程。
1.2.2 对称加密方案(Symmetric encryption schemes)
我们前面只是简单介绍了一下加密方案,具体该怎么加密和解密呢?对称加密是一种加密方法,其中加密和解密使用相同的密钥。
- 共享秘密密钥(Shared Secret Key):Alice 和 Bob 事先商定一个密钥 K K K(例如,一个密码,如 “7$ghH2px”)。
- 加密(Encryption):Alice 使用密钥 K K K将她的消息 M M M(明文)加密成密文 C C C。例如:“Attack at dawn” 加上密钥 K 变成 “xY9!q2#v”。
- 解密(Decryption):Bob 使用相同的密钥 K K K将密文 C C C解密回明文 M M M。
1.2.2.1 替换密码
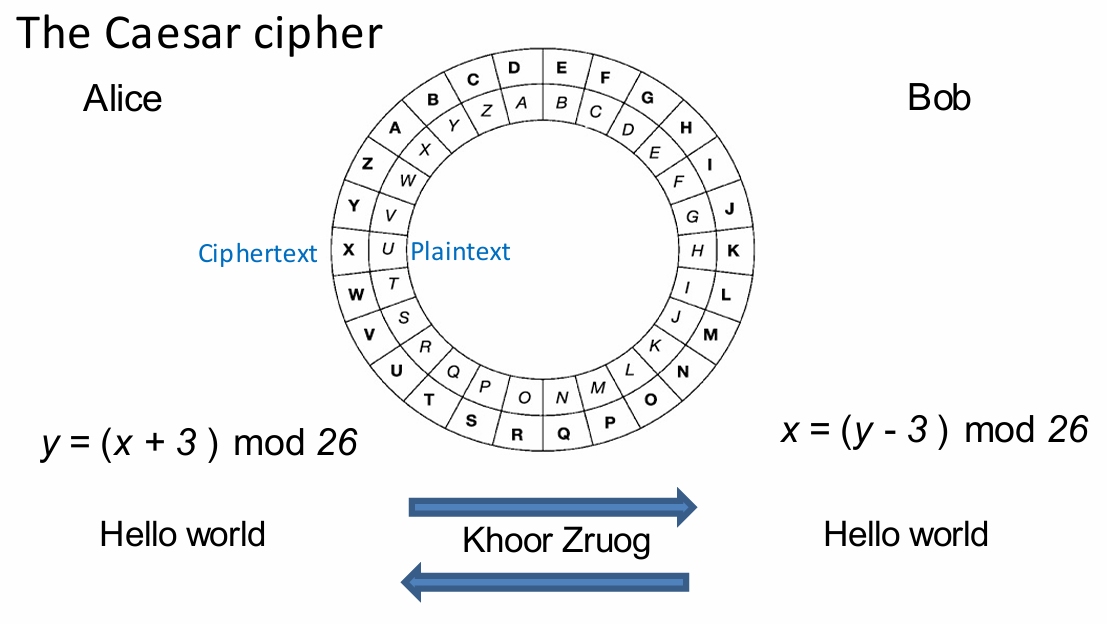
下面介绍凯撒密码(Caesar cipher),一种古老的加密方法。
这是一种简单的替换密码,通过将字母表中的每个字母移动一定数量的位置来进行加密。
每个字母被替换为字母表中向后移动
k
k
k个位置的另一个字母。
公式:
y
=
(
x
+
k
)
m
o
d
n
y=(x+k) \ mod \ n
y=(x+k) mod n
其中
n
n
n是字母表的大小(对于英文字母表,
n
=
26
n=26
n=26),
x
x
x是原始字母(例如,
A
=
0
,
B
=
1
,
.
.
.
,
Z
=
25
A=0, B=1, ..., Z=25
A=0,B=1,...,Z=25),
k
k
k是密钥(例如,
k
=
3
k=3
k=3),
1
≤
k
<
n
1≤k<n
1≤k<n。
假设
k
=
3
k=3
k=3,那么:
A
(
0
)
A (0)
A(0)变为
D
(
3
)
D (3)
D(3),
B
(
1
)
B (1)
B(1)变为
E
(
4
)
E (4)
E(4),
…
Z
(
25
)
Z (25)
Z(25)变为
C
C
C(
28
m
o
d
26
=
2
28 mod 26 = 2
28mod26=2)。
当字母移动超过字母表的末尾时,会“环绕”回到字母表的开头。例如,
Z
(
25
)
Z (25)
Z(25) 移动
3
3
3位后变为
C
(
2
)
C (2)
C(2)。
这是一种替换密码的方案,使用起来非常简单。它们通过将明文中的每个字母替换为字母表中的另一个字母来加密信息。
尽管替换密码易于使用,但它们并不安全。这是因为替换密码的密钥很容易被破解。
常见的方法是频率分析(frequency analysis)。频率分析攻击利用对明文语言的统计知识来破解单字母替换密码。
例如,在英语中,最常见的字母是 ‘e’、‘t’、‘o’ 等,最常见的双字母组合(digrams)是 ‘th’、‘in’、‘er’ 等,最常见的三字母组合(trigrams)是 ‘the’、‘ing’、‘and’ 等。
下图展示了一个密文的例子。

根据频率分析,首先猜测 ‘LBO’ 代表 ‘THE’。
假设 ‘LBO’ 代表 ‘THE’,将 ‘L’ 替换为 ‘T’,‘B’ 替换为 ‘H’,‘O’ 替换为 ‘E’。
最后我们就可以靠暴力破解(Brute force),即尝试所有可能的密钥直到找到正确的密钥。
明文字母表:A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
密文字母表:X Y Z A B C D E F G H I J K L M N O P Q R S T U V W X
也就是将字母表中的每个字母向后移动了3位。
原始文本如下。

1.2.2.2 一次性密码本(One-time pad)
一次性密码本是一种对称加密方法,被认为是最安全的密码之一。
在这种加密方案中,Alice 和 Bob 共享一个随机比特串
K
K
K,这个比特串的长度与他们将要发送的任何消息一样长。
这个密钥
K
K
K用作加密和解密过程中的对称密钥。
密钥的长度应该大于或等于消息的长度。
密钥必须是一次性的,即每次通信时都生成一个新的随机密钥。
一次性密码本加密方法如下:
- 为了加密消息
M
M
M,Alice 计算
C
=
M
⊕
K
C=M⊕K
C=M⊕K,其中
⊕
⊕
⊕表示按位“异或”(exclusive-or)操作。其中:
0 ⊕ 0 = 0 , 0 ⊕ 1 = 1 , 1 ⊕ 0 = 1 , 1 ⊕ 1 = 0 0⊕0=0, 0⊕1=1, 1⊕0=1, 1⊕1=0 0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0
密钥 K K K是一个随机的比特串,长度至少与明文相同。且密钥 K K K必须随机生成,并且每次通信时都不同。
加密: C = M ⊕ K C=M⊕K C=M⊕K
解密: M = C ⊕ K M=C⊕K M=C⊕K
通信是安全的,因为密文 C C C在计算上与随机比特串无法区分(这高度依赖于 K K K被随机选择的事实)。
如图所示。
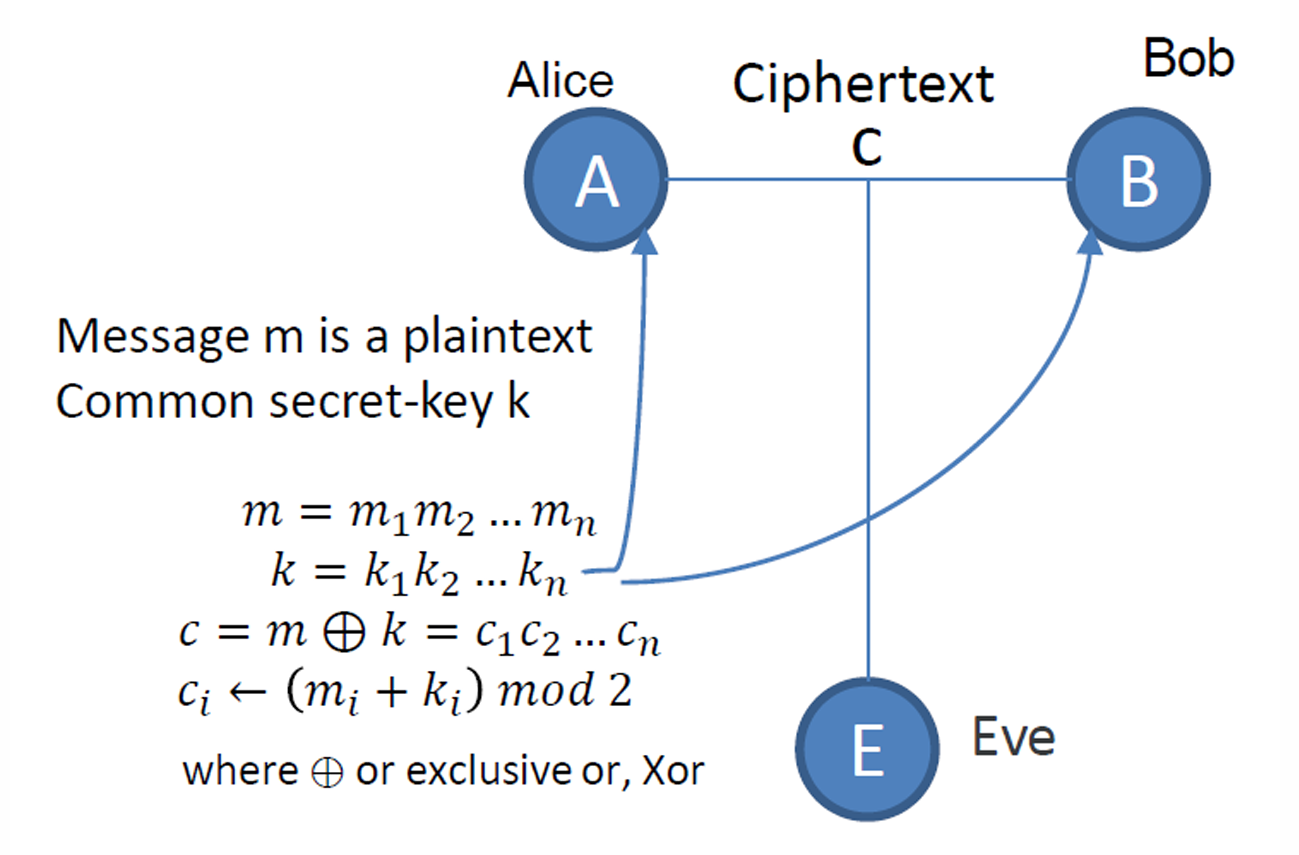
信息 m m m表示为 m 1 m 2 . . . m n m_1m_2...m_n m1m2...mn,密钥 k k k表示为 k 1 k 2 . . k n k_1k_2..k_n k1k2..kn,密文则为 c = m ⊕ k = c 1 c 2 . . . c n c=m⊕k=c_1c_2...c_n c=m⊕k=c1c2...cn,其中 c i ← ( m i + k i ) m o d 2 c_i←(m_i+k_i) \ mod \ 2 ci←(mi+ki) mod 2。
下图展示了一个例子。
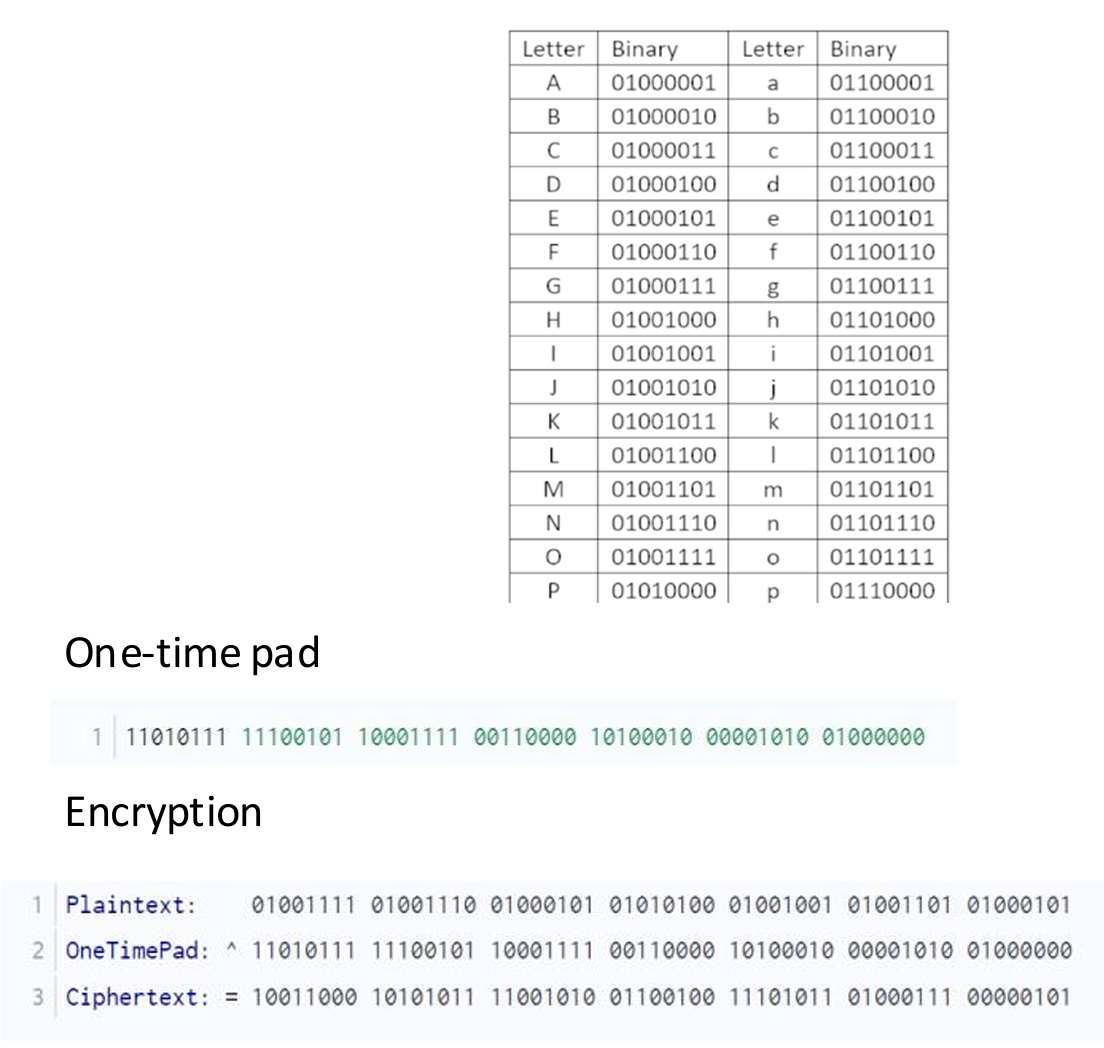
为什么再用密钥可以解密密文呢?
因为
C
⊕
K
=
(
M
⊕
K
)
⊕
K
=
M
⊕
(
K
⊕
K
)
=
M
⊕
0
=
M
C⊕K=(M⊕K)⊕K=M⊕(K⊕K)=M⊕0=M
C⊕K=(M⊕K)⊕K=M⊕(K⊕K)=M⊕0=M
由于异或操作的性质,
K
⊕
K
=
0
K⊕K=0
K⊕K=0(任何比特串与其自身异或的结果是全零字符串)。
因此,
M
⊕
0
=
M
M⊕0=M
M⊕0=M(任何比特串与全零字符串异或的结果是其自身)。
所以一次性密码本的关键在于密钥
K
K
K是随机生成的且密钥
K
K
K不会重复使用(Not-reused)。
因此上面的例子的解密过程如下。

解密结果与原文一致。
一次性密码本的优点:
- 计算效率高:因为按位异或操作(exclusive-or)很容易执行。
- 非常安全:前提是密钥 K 被随机选择。
缺点:
- 需要共享一个非常长的密钥:Alice 和 Bob 必须共享一个与消息长度相同的密钥 K K K。
- 安全性依赖于密钥只使用一次:一次性密码本的安全性基于密钥只被使用一次的事实。
在实践中,我们更倾向于使用可以重复使用的密钥,并且这些密钥通常比我们需要传输的消息短得多。
1.2.3 公钥密码系统
公钥密码系统使用一对密钥:一个公钥和一个私钥。
公钥可以公开分享给任何人,而私钥必须保密,只有密钥的持有者才能解密使用公钥加密的消息。
钥密码学解决了密钥分发的问题,因为公钥可以公开,而私钥保持秘密。
公钥密码系统的组成如下。
- 加密函数(Encryption function
E
E
E):
这是一个将明文(plaintext)转换为密文(ciphertext)的函数。 - 解密函数(Decryption function
D
D
D):
这是一个将密文转换回明文的函数。
公钥密码系统的性质
对于任何消息 M M M,公钥密码系统必须满足以下性质:
1.解密加密后再解密等于原始消息,即 D ( E ( M ) ) = M D(E(M))=M D(E(M))=M。
2.加密 E E E和解密 D D D都很容易计算。
3.从加密函数 E E E推导出解密函数 D D D在计算上是不可行的。
4.先使用解密函数 D D D解密消息 M M M,然后使用加密函数 E E E加密,你会得到原始消息 M M M,即 E ( D ( M ) ) = M E(D(M))=M E(D(M))=M。
公钥密码系统中的加密方法(Encryption method)是公开的,即任何人都可以知道如何使用公钥
E
E
E来加密消息。
尽管加密方法是公开的,但只有持有私钥的人才能解密消息。这意味着即使攻击者知道加密方法,也无法解密消息,因为他们没有私钥。
由于加密过程是公开的,而解密过程是保密的,这种加密方法被称为单向函数。这意味着从加密过程无法轻易推导出解密过程。
在这种加密方法中,加密函数
E
E
E是公开的(public),而解密函数
D
D
D是保密的(private)。

1.2.3.1 图灵密码(Turing’s code)
明文
M
M
M使用公钥
e
e
e和
n
n
n通过以下操作加密:
C
←
M
×
e
m
o
d
n
C←M×e \ mod \ n
C←M×e mod n。这里,
C
C
C是密文,
e
e
e是公钥指数,
n
n
n是模数。
密文
C
C
C通过以下操作解密回明文
M
M
M:
M
←
C
×
d
m
o
d
n
M←C×d \ mod \ n
M←C×d mod n。
这里如果
d
≡
e
−
1
m
o
d
n
d≡e^{-1}\ mod \ n
d≡e−1 mod n,即
d
d
d是
e
e
e模
n
n
n的乘法逆元,那么这个方案可以传输消息。
然而,计算模乘法逆元是容易的,所以这个密码系统不安全,并且从未被实际使用过。
1.2.3.2 RSA加密算法
明文
M
M
M通过公钥
e
e
e和
n
n
n进行加密,操作如下:
C
←
M
e
m
o
d
n
C←M^e \ mod \ n
C←Me mod n
密文
C
C
C通过私钥
d
d
d进行解密,操作如下:
M
←
C
d
m
o
d
n
M←C^d \ mod \ n
M←Cd mod n
选择
e
e
e,
n
n
n,和
d
d
d使得对于每个整数
0
≤
x
<
n
0≤x<n
0≤x<n,我们有:
x
e
d
≡
x
m
o
d
n
x^{ed} ≡x \ mod \ n
xed≡x mod n
从公钥
e
e
e和
n
n
n推导出私钥
d
d
d应该是计算上不可行的。
1.2.3.2.1 费马小定理(Fermat’s Little Theorem)
费马小定理表述如下:设
p
p
p是一个素数,
x
x
x是一个整数,且
x
m
o
d
p
≠
0
x \ mod \ p ≠ 0
x mod p=0。那么:
x
p
−
1
≡
1
(
m
o
d
p
)
x ^ {p−1} ≡1(mod \ p)
xp−1≡1(mod p)
例如当
p
=
5
p=5
p=5时。
1
4
m
o
d
5
=
1
1^4 \ mod \ 5 = 1
14 mod 5=1,因为
1
4
=
1
1^4=1
14=1,所以
1
m
o
d
5
=
1
1 \ mod \ 5 = 1
1 mod 5=1
2
4
m
o
d
5
=
1
2^4 \ mod \ 5 = 1
24 mod 5=1,因为
2
4
=
16
2^4=16
24=16,所以
16
m
o
d
5
=
1
16 \ mod \ 5 = 1
16 mod 5=1
3
4
m
o
d
5
=
1
3^4 \ mod \ 5 = 1
34 mod 5=1,因为
3
4
=
81
3^4=81
34=81,所以
81
m
o
d
5
=
1
81 \ mod \ 5 = 1
81 mod 5=1
4
4
m
o
d
5
=
1
4^4 \ mod \ 5 = 1
44 mod 5=1,因为
4
4
=
256
4^4=256
44=256,所以
256
m
o
d
5
=
1
256 \ mod \ 5 = 1
256 mod 5=1
证明过程如下:
首先是集合
Z
p
∗
=
{
1
,
2
,
.
.
.
,
p
−
1
}
Z_p^*=\{1,2,...,p-1\}
Zp∗={1,2,...,p−1}
由于
g
c
d
(
x
,
p
)
=
1
gcd(x,p)=1
gcd(x,p)=1,
x
x
x与
p
p
p互质,因此将集合
S
S
S中的所有数乘以
x
x
x会重新排列这个集合:
x
Z
p
∗
=
{
x
⋅
1
m
o
d
p
,
x
⋅
2
m
o
d
p
,
…
,
x
⋅
(
p
−
1
)
m
o
d
p
}
=
{
1
,
2
,
…
,
p
−
1
}
xZ_p^*=\{x⋅1 \ mod \ p,x⋅2 \ mod \ p,…,x⋅(p−1) \ mod \ p\}=\{1,2,…,p−1\}
xZp∗={x⋅1 mod p,x⋅2 mod p,…,x⋅(p−1) mod p}={1,2,…,p−1}
将原始集合和重排后的集合中的所有数相乘:
1
⋅
2
⋅
…
⋅
(
p
−
1
)
≡
(
x
⋅
1
)
⋅
(
x
⋅
2
)
⋅
…
⋅
(
x
⋅
(
p
−
1
)
)
m
o
d
p
1⋅2⋅…⋅(p−1)≡(x⋅1)⋅(x⋅2)⋅…⋅(x⋅(p−1)) \ mod \ p
1⋅2⋅…⋅(p−1)≡(x⋅1)⋅(x⋅2)⋅…⋅(x⋅(p−1)) mod p
化简得到:
(
p
−
1
)
!
≡
x
p
−
1
⋅
(
p
−
1
)
!
m
o
d
p
(p−1)!≡x^p−1 ⋅(p−1)! \ mod \ p
(p−1)!≡xp−1⋅(p−1)! mod p
由于
g
c
d
(
(
p
−
1
)
!
,
p
)
=
1
gcd((p−1)!,p)=1
gcd((p−1)!,p)=1,
(
p
−
1
)
!
(p−1)!
(p−1)!在模
p
p
p下有乘法逆元。因此,我们可以将等式两边乘以
(
p
−
1
)
!
(p−1)!
(p−1)!的逆元:
x
p
−
1
≡
1
m
o
d
p
x^{p−1} ≡1 \ mod \ p
xp−1≡1 mod p
为此我们可以得到一个推论:
由于
x
p
−
1
≡
1
m
o
d
p
x^{p−1}≡1 \ mod \ p
xp−1≡1 mod p,我们可以将等式重写为
x
p
−
2
≡
x
−
1
m
o
d
p
x^{p−2} ≡x^{−1} \ mod \ p
xp−2≡x−1 mod p。
因此,
x
−
1
x^{-1}
x−1可以表示为
x
p
−
2
m
o
d
p
x^{p−2} \ mod \ p
xp−2 mod p。
我们可以根据乘法逆元的定义得到这个推论。
1.2.3.2.2 欧拉函数
乘法群(the multiplicative group)
Z
n
∗
Z_n^*
Zn∗包含所有在
Z
n
Z_n
Zn中与n互质的数。
例如,如果
n
=
10
n=10
n=10,则与
10
10
10互质的数是
1
,
3
,
7
,
9
1,3,7,9
1,3,7,9,即
Z
10
∗
=
{
1
,
3
,
7
,
9
}
Z_{10}^*=\{1,3,7,9\}
Z10∗={1,3,7,9}。
欧拉函数用于计算与给定整数
n
n
n互质的正整数的数量。
因此按照上面的例子
ϕ
(
10
)
=
4
ϕ(10)=4
ϕ(10)=4。
如果
p
p
p是一个质数,那么
ϕ
(
p
)
=
p
−
1
ϕ(p)=p-1
ϕ(p)=p−1
假设
n
n
n的素因子分解为
n
=
p
1
k
1
×
p
2
k
2
×
…
×
p
m
k
m
n=p_1^{k_1}×p_2^{k_2}×…×p_m^{k_m}
n=p1k1×p2k2×…×pmkm
欧拉函数
ϕ
(
n
)
ϕ(n)
ϕ(n)的计算公式为:
ϕ
(
n
)
=
n
×
(
1
−
1
/
p
1
)
×
(
1
−
1
/
p
2
)
×
…
×
(
1
−
1
/
p
m
)
ϕ(n)=n×(1-1/p_1)×(1-1/p_2)×…×(1-1/p_m)
ϕ(n)=n×(1−1/p1)×(1−1/p2)×…×(1−1/pm)
例子如下:
15
=
3
×
5
15 = 3×5
15=3×5,
ϕ
(
n
)
=
15
×
(
1
−
1
/
3
)
×
(
1
−
1
/
5
)
=
15
×
(
2
/
3
)
×
(
4
/
5
)
=
8
ϕ(n)= 15 × (1 - 1 / 3) × (1 - 1 / 5) = 15 × (2 / 3) × (4 / 5) = 8
ϕ(n)=15×(1−1/3)×(1−1/5)=15×(2/3)×(4/5)=8
12
=
2
2
×
3
12 = 2 ^ 2 × 3
12=22×3,
ϕ
(
n
)
=
12
×
(
1
−
1
/
2
)
×
(
1
−
1
/
3
)
=
4
ϕ(n)= 12 × (1 - 1 / 2) × (1 - 1 / 3) = 4
ϕ(n)=12×(1−1/2)×(1−1/3)=4
所以如果
n
=
p
×
q
n = p × q
n=p×q(
p
p
p和
q
q
q是质数),那么
ϕ
(
n
)
=
n
×
(
1
−
1
/
p
)
×
(
1
−
1
/
q
)
=
p
q
×
(
p
−
1
)
/
q
×
(
q
−
1
)
/
q
=
(
p
−
1
)
(
q
−
1
)
ϕ(n)= n × (1 - 1 / p) × (1 - 1 / q) = pq × (p-1)/q × (q-1)/q = (p-1)(q-1)
ϕ(n)=n×(1−1/p)×(1−1/q)=pq×(p−1)/q×(q−1)/q=(p−1)(q−1)
1.2.3.2.3 欧拉定理
设
n
n
n是一个正整数,
x
x
x是一个整数,满足
g
c
d
(
x
,
n
)
=
1
gcd(x,n)=1
gcd(x,n)=1(即 x 和 n 互质)。那么:
x
ϕ
(
n
)
≡
1
m
o
d
n
x^{ϕ(n)} ≡1 \ mod \ n
xϕ(n)≡1 mod n
例如,当
n
=
10
n=10
n=10时。
x
=
3
,
3
ϕ
(
10
)
m
o
d
10
=
3
4
m
o
d
10
=
81
m
o
d
10
=
1
x=3, 3^{ϕ(10)} \ mod \ 10 = 3^4 \ mod \ 10 = 81 \ mod \ 10 = 1
x=3,3ϕ(10) mod 10=34 mod 10=81 mod 10=1
x
=
7
,
7
ϕ
(
10
)
m
o
d
10
=
7
4
m
o
d
10
=
2401
m
o
d
10
=
1
x=7, 7^{ϕ(10)} \ mod \ 10 = 7^4 \ mod \ 10 = 2401 \ mod \ 10 = 1
x=7,7ϕ(10) mod 10=74 mod 10=2401 mod 10=1
x
=
9
,
9
ϕ
(
10
)
m
o
d
10
=
7
4
m
o
d
10
=
6561
m
o
d
10
=
1
x=9, 9^{ϕ(10)} \ mod \ 10 = 7^4 \ mod \ 10 = 6561 \ mod \ 10 = 1
x=9,9ϕ(10) mod 10=74 mod 10=6561 mod 10=1
证明如下:
我们首先有
Z
n
∗
=
{
a
1
=
1
<
a
2
<
a
ϕ
(
n
)
}
Z_n^*=\{a_1=1<a_2<a_{ϕ(n)}\}
Zn∗={a1=1<a2<aϕ(n)}
由于
g
c
d
(
x
,
n
)
=
1
gcd(x,n)=1
gcd(x,n)=1将集合中的每个元素乘以
x
x
x并模
n
n
n,会重新排列这个集合,
{
x
⋅
a
1
m
o
d
n
,
x
⋅
a
2
m
o
d
n
,
.
.
.
,
x
⋅
a
ϕ
(
n
)
m
o
d
n
}
=
{
a
1
,
a
2
,
.
.
.
,
a
ϕ
(
n
)
}
\{x⋅a_1 \ mod n, x ⋅ a_2 \ mod \ n,...,x⋅a_{ϕ(n)} \ mod \ n\} = \{a_1,a_2,...,a_{ϕ(n)}\}
{x⋅a1 modn,x⋅a2 mod n,...,x⋅aϕ(n) mod n}={a1,a2,...,aϕ(n)}
将原始集合和重排后的集合中的所有元素相乘:
∏
i
=
1
ϕ
(
n
)
a
i
=
∏
i
=
1
ϕ
(
n
)
(
x
⋅
a
i
)
m
o
d
p
≡
x
ϕ
(
n
)
∏
i
=
1
ϕ
(
n
)
a
i
m
o
d
n
\prod_{i=1}^{\phi(n)} a_i = \prod_{i=1}^{\phi(n)} (x \cdot a_i) \mod p \equiv x^{\phi(n)} \prod_{i=1}^{\phi(n)} a_i \mod n
∏i=1ϕ(n)ai=∏i=1ϕ(n)(x⋅ai)modp≡xϕ(n)∏i=1ϕ(n)aimodn
这表明:
∏
i
=
1
ϕ
(
n
)
a
i
≡
x
ϕ
(
n
)
m
o
d
n
\prod_{i=1}^{\phi(n)} a_i \equiv x^{\phi(n)} \mod n
∏i=1ϕ(n)ai≡xϕ(n)modn
由于
g
c
d
(
∏
i
=
1
ϕ
(
n
)
a
i
,
n
)
=
1
gcd(\prod_{i=1}^{\phi(n)} a_i,n)=1
gcd(∏i=1ϕ(n)ai,n)=1,
∏
i
=
1
ϕ
(
n
)
a
i
\prod_{i=1}^{\phi(n)} a_i
∏i=1ϕ(n)ai在模 (n) 下有乘法逆元。因此,我们可以将等式两边乘以
∏
i
=
1
ϕ
(
n
)
a
i
\prod_{i=1}^{\phi(n)} a_i
∏i=1ϕ(n)ai 的逆元:
x
ϕ
(
n
)
≡
1
m
o
d
n
x^{\phi(n)} \equiv 1 \mod n
xϕ(n)≡1modn
1.2.3.2.4 RSA加密算法
所以我们现在回到RSA算法。
加密:使用公钥
e
e
e和模数
n
n
n进行加密:
C
←
M
e
m
o
d
n
C←M^e \ mod \ n
C←Me mod n。
解密:使用私钥
d
d
d进行解密:
M
←
C
d
m
o
d
n
)
M←C^d \ mod \ n)
M←Cd mod n)。
欧拉定理的应用:根据欧拉定理,如果
x
x
x和
n
n
n互质(即
g
c
d
(
x
,
n
)
=
1
gcd(x,n)=1
gcd(x,n)=1),那么
x
ϕ
(
n
)
+
1
≡
1
m
o
d
n
x^{ϕ(n)+1}≡1 \ mod \ n
xϕ(n)+1≡1 mod n,其中
ϕ
(
n
)
ϕ(n)
ϕ(n)是欧拉函数。
选择密钥:选择
d
d
d,
e
e
e,和
k
k
k使得
d
e
=
k
ϕ
(
n
)
+
1
de=kϕ(n)+1
de=kϕ(n)+1。
进一步假设
g
c
d
(
e
,
ϕ
(
n
)
+
1
)
=
1
gcd(e,ϕ(n)+1)=1
gcd(e,ϕ(n)+1)=1,这确保了
e
e
e与
ϕ
(
n
)
+
1
ϕ(n)+1
ϕ(n)+1互质,从而可以找到
e
e
e的乘法逆元
e
m
o
d
ϕ
(
n
)
e \ mod \ ϕ(n)
e mod ϕ(n)。
给定
e
e
e和
n
n
n后,找到
d
d
d是困难的。我们知道,给定
k
+
1
k+1
k+1,可以通过扩展欧几里得算法找到解。
因此,我们必须选择
n
n
n,使得
k
+
1
k+1
k+1难以计算。
对于大的
n
n
n(两个大素数的成绩),找到
d
d
d是计算上不可行的,因为需要进行大数分解,这是目前已知的计算难题。
因此RSA加密算法的步骤如下:
系统设置:
- 选择两个大素数:首先选择两个大的素数 p p p和 q q q。
- 计算 n n n和 ϕ ( n ) ϕ(n) ϕ(n):计算 n = p × q n=p×q n=p×q, ϕ ( n ) = ( p − 1 ) ( q − 1 ) ϕ(n)=(p−1)(q−1) ϕ(n)=(p−1)(q−1)。
- 选择公钥和私钥:选择两个数
e
e
e和
d
d
d,使得:
e e e和 ϕ ( n ) ϕ(n) ϕ(n)互质,这样 e e e就有模 ϕ ( n ) ϕ(n) ϕ(n)的乘法逆元。
d e ≡ 1 m o d ϕ ( n ) de≡1 \ mod \ ϕ(n) de≡1 mod ϕ(n),这意味着 d d d是 e e e模 ϕ ( n ) ϕ(n) ϕ(n)的乘法逆元 - 公钥由 e e e和 n n n组成。私钥是 d d d。
加密过程:
- 明文 M M M的范围:明文 M M M必须是 Z n Z_n Zn中的元素,即 0 ≤ M < n 0≤M<n 0≤M<n。
- 加密:使用公钥 e e e和 n n n进行加密: C = M e m o d n C=M^e \ mod \ n C=Me mod n,得到密文 C C C。
解密过程:
- 解密:使用私钥 d d d进行解密: M = C d m o d n M=C^d \ mod \ n M=Cd mod n,恢复出原始明文 M M M。
例子如下:
系统设置:
p
=
7
,
q
=
17
,
n
=
7
×
17
=
119
,
ϕ
(
119
)
=
6
×
16
=
96
,
e
=
5
,
d
=
77
(
77
×
5
=
96
×
4
+
1
)
p=7,q=17,n=7 ×17=119, ϕ(119) = 6 ×16=96,e=5,d=77(77×5=96×4+1)
p=7,q=17,n=7×17=119,ϕ(119)=6×16=96,e=5,d=77(77×5=96×4+1)
因此我们获得了公钥
K
E
=
(
119
,
5
)
K_E=(119,5)
KE=(119,5),私钥
K
D
=
77
K_D=77
KD=77。
加密过程:如果
M
=
19
M=19
M=19,那么
C
=
19
5
m
o
d
119
=
66
C=19^5 \ mod \ 119 =66
C=195 mod 119=66。
解密过程:
M
=
66
77
m
o
d
119
=
19
M = 66^{77} \ mod \ 119 = 19
M=6677 mod 119=19
下图展示了另一个更完整的例子。

1.2.3.2.5 快速指数运算(Fast Exponentiation)
RSA算法的一个潜在瓶颈是计算形式为
x
k
m
o
d
n
x^k \ mod \ n
xk mod n的表达式。
一种简单直接的方法是计算
x
2
m
o
d
n
x^2 \ mod \ n
x2 mod n,然后使用这个结果来计算
x
3
m
o
d
n
x^3 \ mod \ n
x3 mod n,接着计算
x
4
m
o
d
n
x^4 \ mod \ n
x4 mod n,依此类推。
这种方法的复杂度是
O
(
k
)
O(k)
O(k)。
我们现在介绍一种快速指数运算的方法。
我们以
3
9
4
m
o
d
17
3^94 \ mod \ 17
394 mod 17为例。
首先任何数字都可以表示为不同二的幂次方的和。(所以有二进制)
例如,
94
94
94可以分解为
64
+
16
+
8
+
4
+
2
64+16+8+4+2
64+16+8+4+2,即
94
=
2
6
+
2
4
+
2
3
+
2
2
+
2
1
94=2^6+2^4+2^3+2^2+2^1
94=26+24+23+22+21
因此我们现在可以利用前面我们学的性质进行简化,我们先计算:
3
2
≡
9
m
o
d
17
3^2 ≡ 9 \ mod \ 17
32≡9 mod 17
3
4
≡
81
≡
13
≡
−
4
m
o
d
17
3^4 ≡ 81 ≡ 13 ≡ -4 \ mod \ 17
34≡81≡13≡−4 mod 17
3
8
≡
(
3
4
)
2
≡
16
≡
−
1
m
o
d
17
3^8 ≡ (3^4)^2 ≡ 16 ≡ -1 \ mod \ 17
38≡(34)2≡16≡−1 mod 17
3
16
≡
(
3
8
)
2
≡
(
−
1
)
2
≡
1
m
o
d
17
3^{16} ≡ (3^8)^2 ≡ (-1)^2 ≡ 1 \ mod \ 17
316≡(38)2≡(−1)2≡1 mod 17
3
64
≡
(
3
16
)
4
≡
(
1
)
4
≡
1
m
o
d
17
3^{64} ≡ (3^{16})^4 ≡ (1)^4 ≡ 1 \ mod \ 17
364≡(316)4≡(1)4≡1 mod 17
因此,简化前面的式子得到
394
≡
3
64
+
16
+
8
+
4
+
2
m
o
d
17
≡
3
64
3
16
3
8
3
4
3
2
m
o
d
17
≡
(
1
)
(
1
)
(
−
1
)
(
−
4
)
(
9
)
m
o
d
17
≡
36
m
o
d
17
≡
2
m
o
d
17
394 ≡ 3^{64+16+8+4+2} \ mod \ 17 ≡ 3^{64}3^{16}3^83^43^2 \ mod \ 17 ≡ (1)(1)(-1)(-4)(9) \ mod \ 17 ≡ 36 \ mod \ 17 ≡ 2 \ mod \ 17
394≡364+16+8+4+2 mod 17≡364316383432 mod 17≡(1)(1)(−1)(−4)(9) mod 17≡36 mod 17≡2 mod 17
我们还可以通过重复平方(repeated squaring)的算法来提高计算
x
k
m
o
d
n
x^k \ mod \ n
xk mod n的效率。
直接计算
x
16
x^{16}
x16可能需要进行
15
15
15次乘法操作。
通过重复平方的方法,可以先计算
x
2
x^2
x2,然后
(
x
2
)
2
=
x
4
(x^2)^2=x^4
(x2)2=x4,接着
(
x
4
)
2
=
x
8
(x^4)^2=x^8
(x4)2=x8,最后
(
x
8
)
2
=
x
16
(x^8)^2=x^{16}
(x8)2=x16这种方法只需要
4
4
4次乘法操作,而不是
15
15
15次。
这种方法的复杂度是
O
(
l
o
g
k
)
O(logk)
O(logk),而不是直接方法的
O
(
k
)
O(k)
O(k)。这是因为每次操作都将指数减半,所以所需的操作次数与指数的对数成正比。
1.3 数字签名(Digital signatures)
数字签名用于验证消息的发送者身份。在这种情况下,Alice想要确认消息
M
M
M是由Bob发送的。
Bob使用他的私钥(解密函数)对消息 M 进行签名:
S
←
M
d
m
o
d
n
S←M^d \ mod \ n
S←Md mod n,这里,
S
S
S是签名,
d
d
d是Bob的私钥,
n
n
n是模数。
Alice使用Bob的公钥(加密函数)来验证数字签名:
M
≡
S
e
m
o
d
n
M≡S^e \ mod \ n
M≡Se mod n,这里,
e
e
e是Bob的公钥。
由于只有Bob知道私钥
d
d
d,因此只有他能够创建有效的签名
S
S
S。
当Alice使用公钥
e
e
e对签名
S
S
S进行解密时,如果结果与原始消息
M
M
M匹配,这验证了消息确实是由Bob发送的。
























 18
18

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








