machine learning个人笔记系列（一）

最新推荐文章于 2021-05-23 20:47:29 发布

seedcup

最新推荐文章于 2021-05-23 20:47:29 发布

阅读量288

点赞数

CC 4.0 BY-SA版权

分类专栏： ml

本文链接：https://blog.youkuaiyun.com/seedcup/article/details/81409871

ml 专栏收录该内容

7 篇文章

订阅专栏

本文介绍了机器学习的基础概念，并通过房价预测实例讲解了单变量线性回归模型的工作原理。文章详细阐述了如何使用梯度下降算法来优化模型参数，以最小化预测误差。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

机器学习入门
- 定义
- 分类
单变量线性回归

向Andrew Ng的机器学习课程致敬

机器学习入门

定义

Arthur Samuel (1959). Machine Learning: Field of study that gives computers the ability to learn without being explicitly programmed.
Tom Mitchell (1998) Well-posed Learning Problem: A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.

单变量线性回归

以房价预测来说明

背景

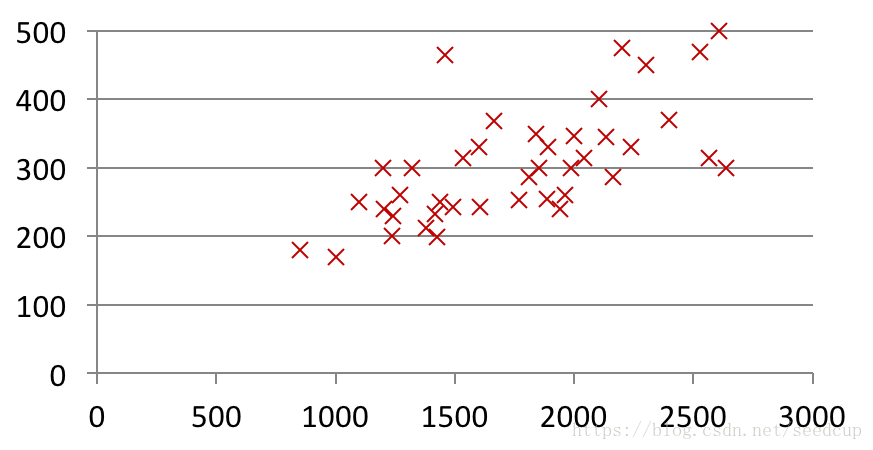
一个学生从波特兰俄勒冈州的研究所收集了一些房价的数据。
如图所示，将这些数据标在坐标上，横轴表示房子的面积，单位是平方英尺，纵轴表示房价，单位是千美元。
基于这组数据，假如你有一个朋友，他有一套 750 平方英尺房子，现在他希望把房子卖掉，能卖多少钱。

这里写图片描述

模型

可以画一条直线，让直线尽可能匹配所有数据。
可能还有更好的，比如我们用二次方程去拟合所有数据，即使用以下模型来模拟面积和售价的关系

h θ (x) = θ 0 + θ 1 x

$h_\theta(x) = \theta_0 + \theta_1x$

这就是一个监督学习的例子。

损益函数

上面的模型中，如果来选择合适的参数 $\theta_0$ 和 $\theta_1$ 来尽量让预测值与真实值接近，那我们的模型就很完美了。
为此，我们定义一个函数来衡量不同参数，其模型与真实值的差异性，这样就能根据这个差异性来选择合适的参数。这个差异性叫做损益函数，对于线性回归模型来说，其损益函数定义如下：

J (θ 0, θ 1) = 1 2 m \sum i = 1 m (h θ (x (i)) - y (i)) 2

$J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)} ) ^ 2$

寻找最合适的参数来使预测最接近真实值就转化为，求损益函数的最小值了。

梯度下降算法

给定上述模型已经损益函数，如何求最小的损益函数对应的参数呢。有一种非常有名的算法，叫梯度下降算法，可以用来求某个函数的全局或局部最小值。其实现过程如下：

初始函数值在某个峰值
随着迭代过程中，这个函数值会一步一步的下降，直至到某个局部最优或者全局最优的值

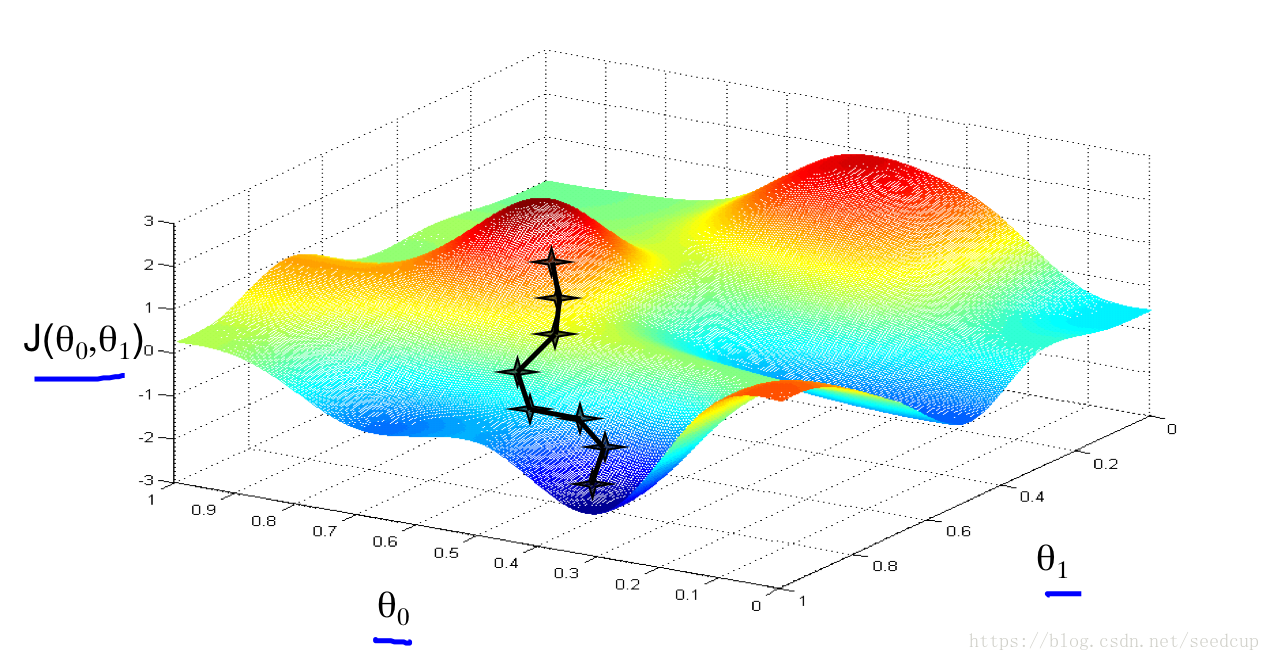
算法具体描述如下：

Gradient descent algorithm

repeated until convergence {

$θ j : = θ j - α \partial \partial θ j J (θ 0, θ 1) f o r (j = 0 a n d j = 1)$ $\theta_j := \theta_j - \alpha \frac{\partial }{\partial \theta_j} J(\theta_0, \theta_1) \qquad for \ (j = 0\ and\ j = 1)$
}

注意：需要同时更新所有的参数，如下所示

$t e m p θ 0 = θ 0 - α \partial \partial θ 0 J (θ 0, θ 1) t e m p θ 1 = θ 1 - α \partial \partial θ 1 J (θ 0, θ 1) θ 0 = t e m p θ 0 θ 1 = t e m p θ 1$ $temp\theta_0 = \theta_0 - \alpha \frac{\partial }{\partial \theta_0} J(\theta_0, \theta_1) \\ temp\theta_1 = \theta_1 - \alpha \frac{\partial }{\partial \theta_1} J(\theta_0, \theta_1) \\ \theta_0 = temp\theta_0 \\ \theta_1 = temp\theta_1$

可以看到这里还有一个参数 $\alpha$ 需要我们来确定，这个参数被称为学习率。

当 $\alpha$ 比较小的时候，需要迭代很多次才能收敛到最小值。
而当 $\alpha$ 比较大的时候，则可能导致梯度下降算法不能收敛，总是在最低值附近徘徊。

学习率对求损益函数的影响如下图所示：

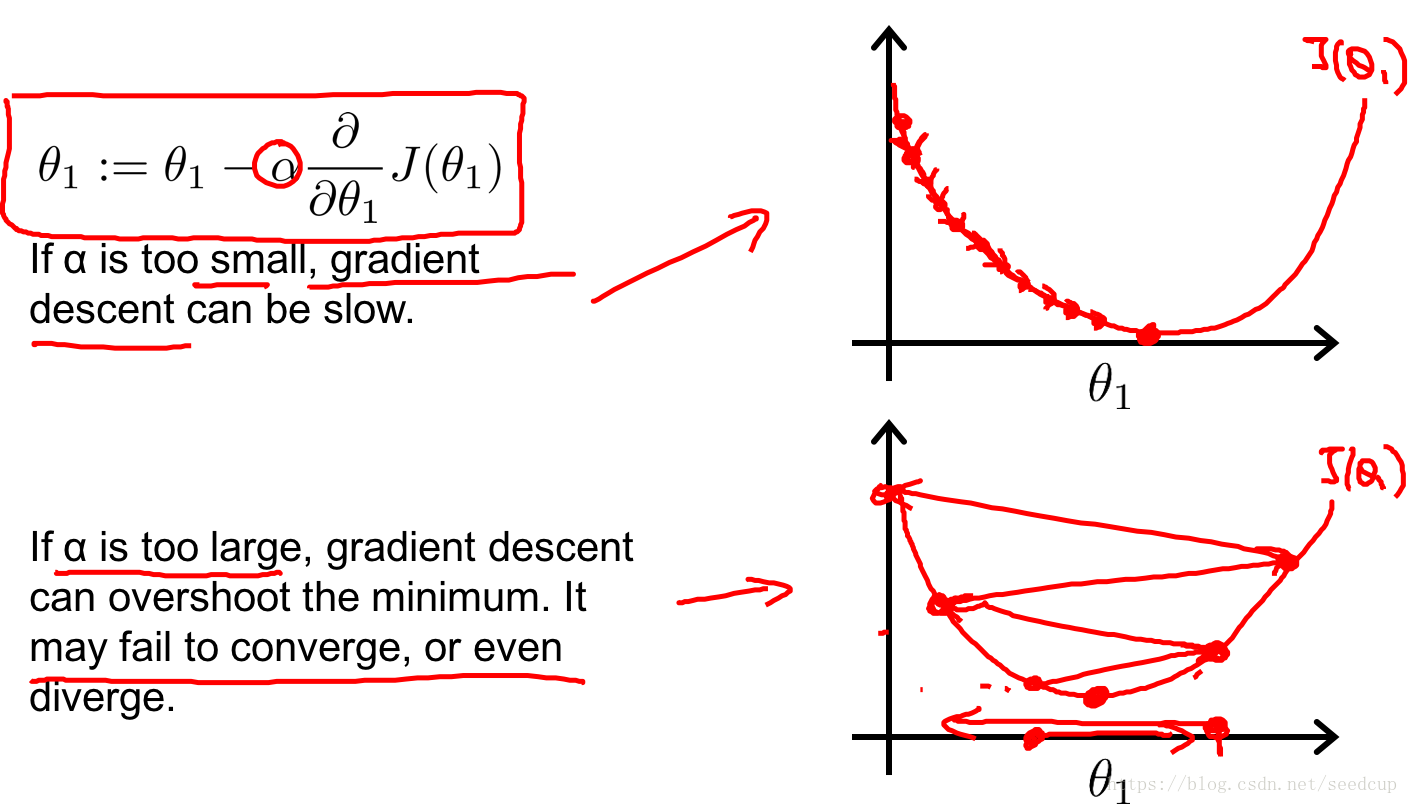
这里写图片描述

一旦选定了学习率后，不用每次迭代都改变学习率的值，因为梯度下降算法会制动调整下降幅度来达到局部最优解。

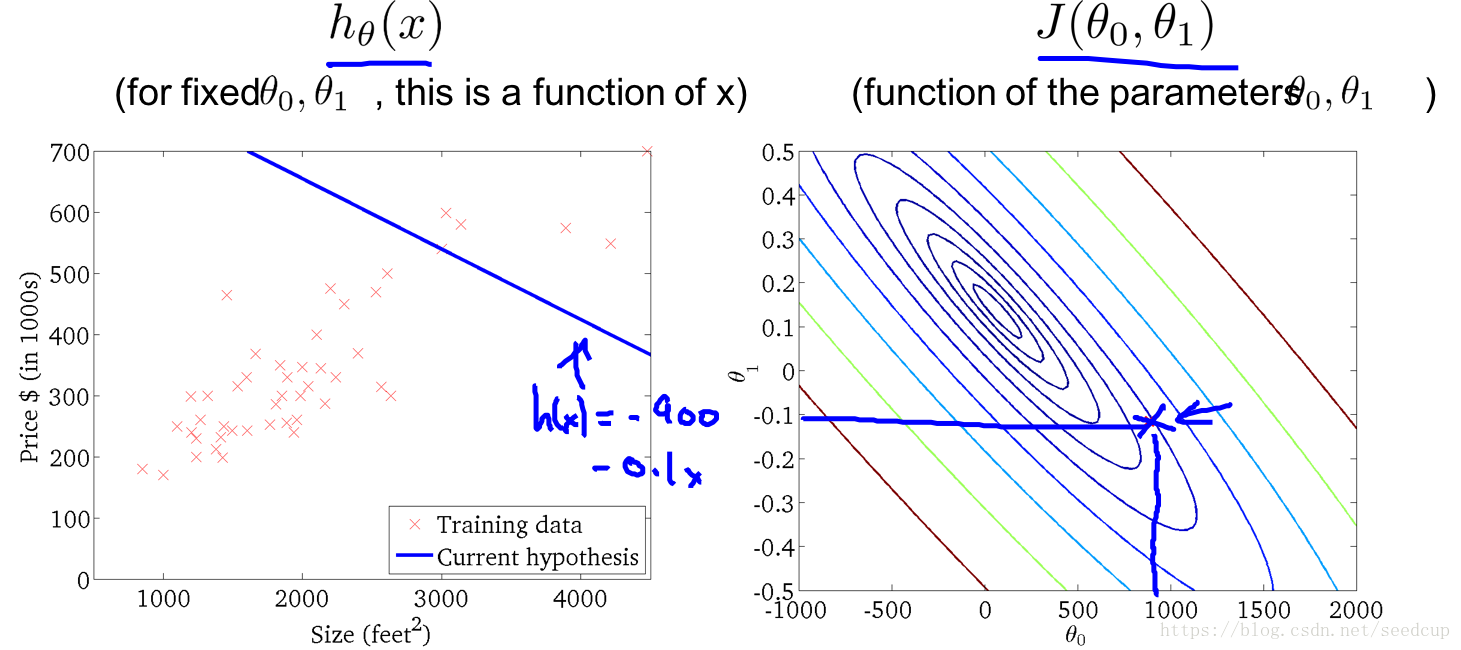
根据上述梯度下降算法描述，再来分析下单变量线性回归如何使用梯度下降算法求最优参数。如下公式所示，是单变量线性回归模型的参数计算方式。

θ 0 = θ 0 - α \partial \partial θ 0 J (θ 0, θ 1) = θ 0 - α 1 m \sum i = 1 m (h θ (x (i)) - y (i)) θ 1 = θ 1 - α \partial \partial θ 1 J (θ 0, θ 1) = θ 0 - α 1 m \sum i = 1 m (h θ (x (i)) - y (i)) x (i)

$\theta_0 = \theta_0 - \alpha\frac{\partial }{\partial \theta_0} J(\theta_0, \theta_1) = \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)} ) \\ \theta_1 = \theta_1 - \alpha \frac{\partial }{\partial \theta_1} J(\theta_0, \theta_1) = \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)} ) x^{(i)}$

随着迭代进行，模型变化过程以下系列图所示：
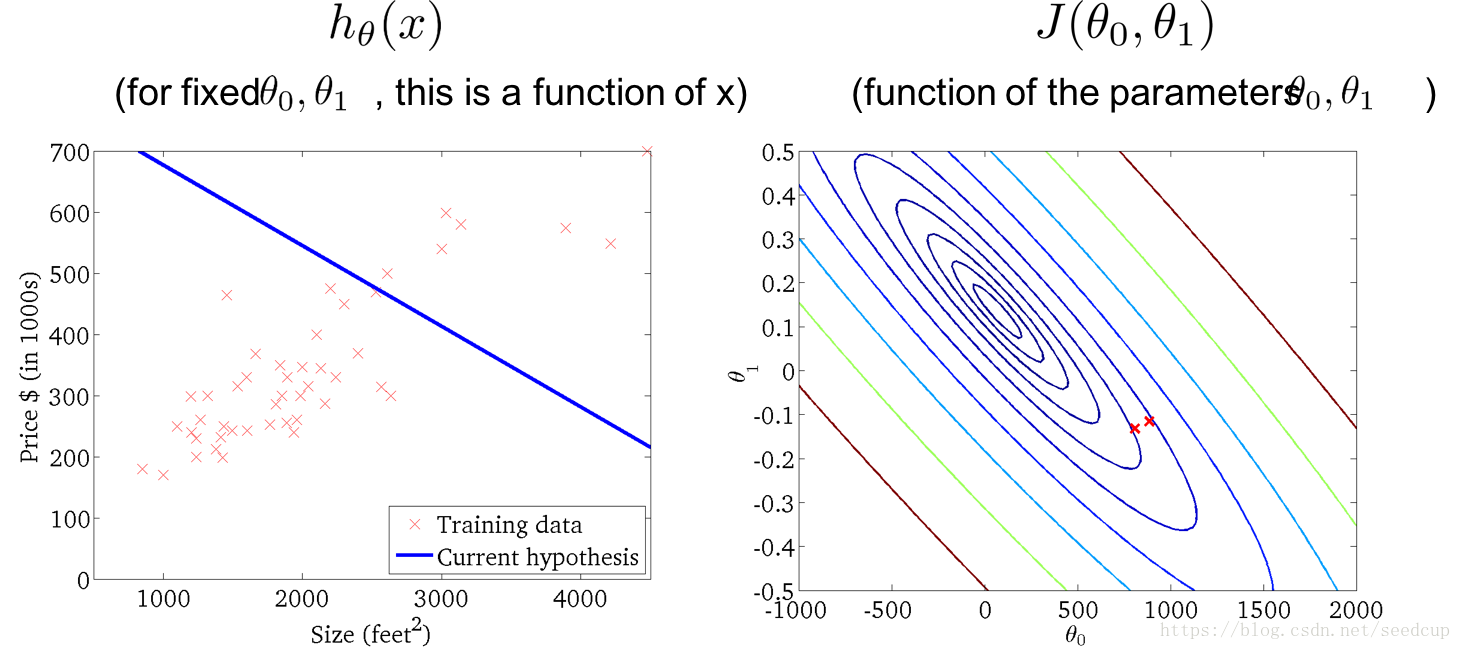
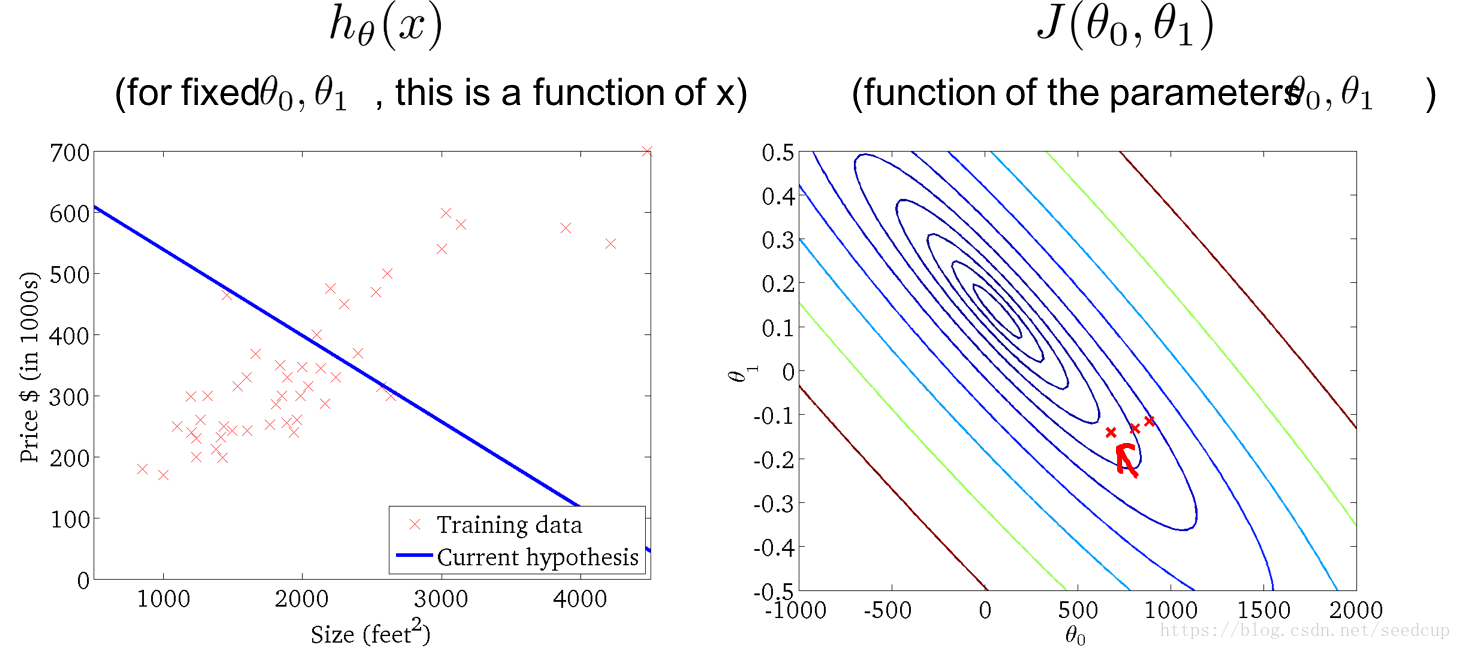
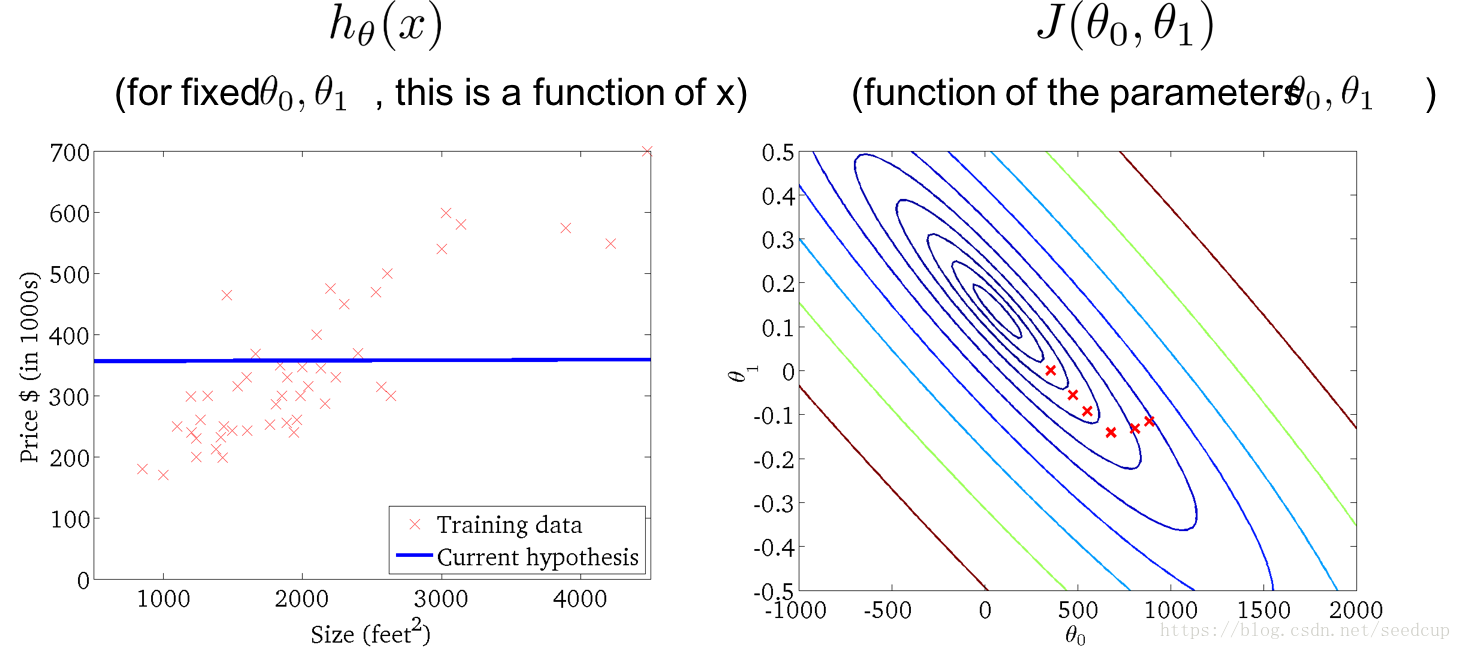
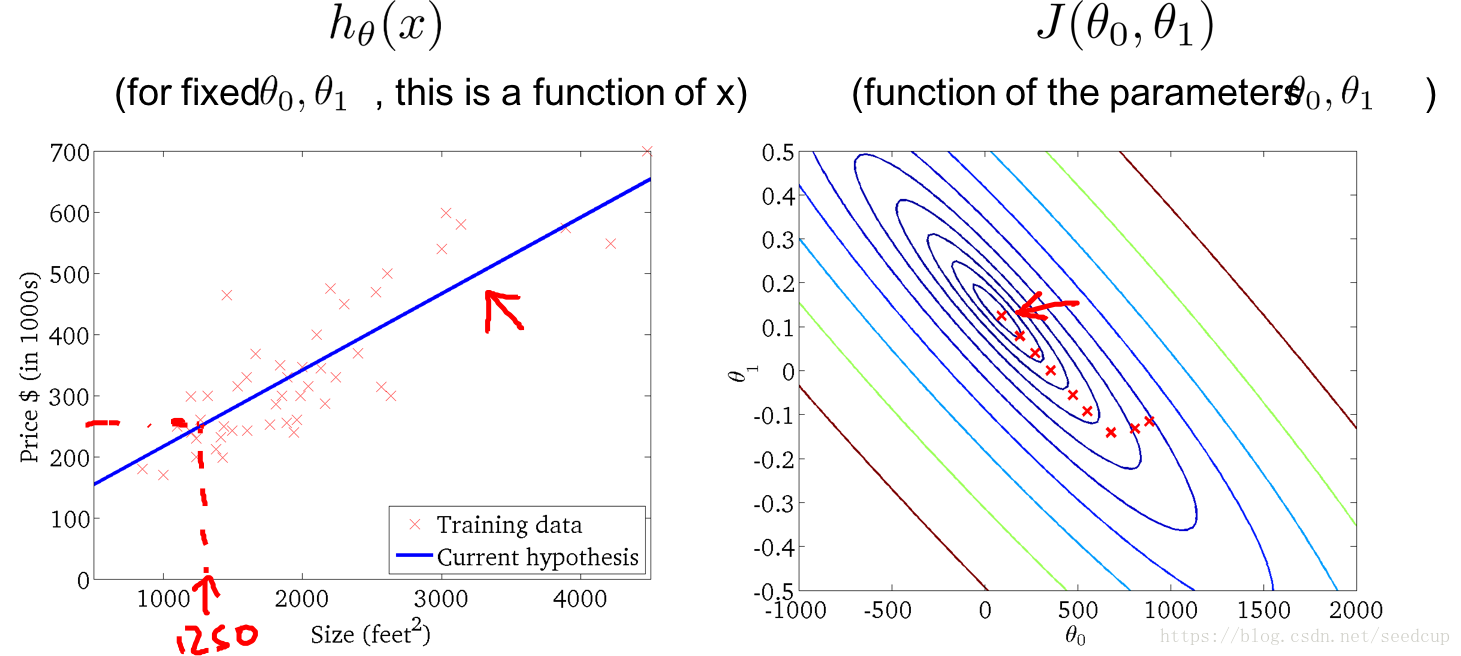
这里写图片描述