算法基础篇（10）递归型枚举与回溯剪枝

搜索，是一种枚举，通过穷举所有情况来找到最优解或者统计合法解的个数。搜索一般分为深度优先搜索（DFS）与 宽度优先搜索（BFS）

回溯：在搜索过程中，遇到走不通或者走到底的情况，就回头

剪枝：剪掉在搜索过程中重复出现或者不是最优解的分支

1、枚举子集

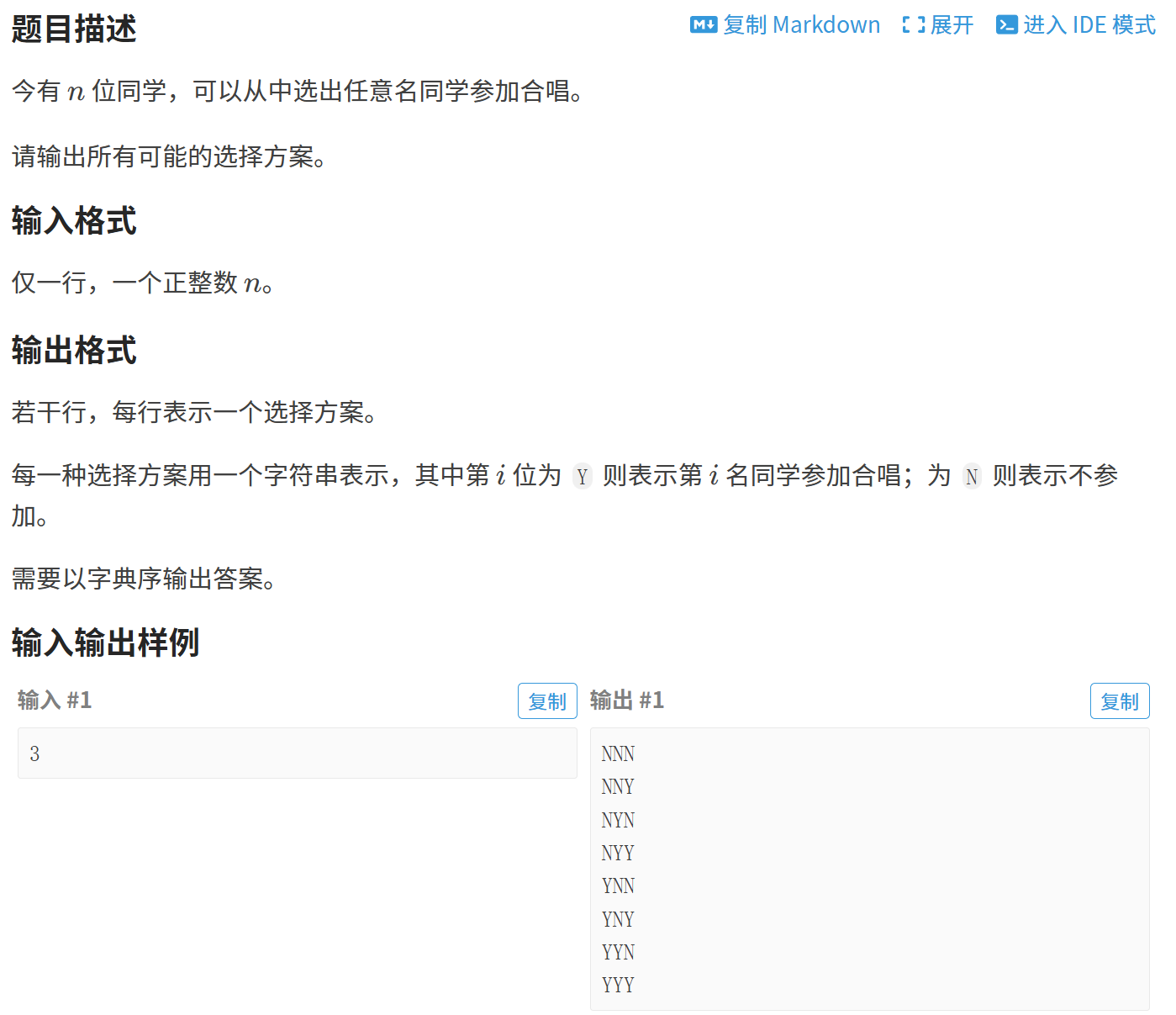
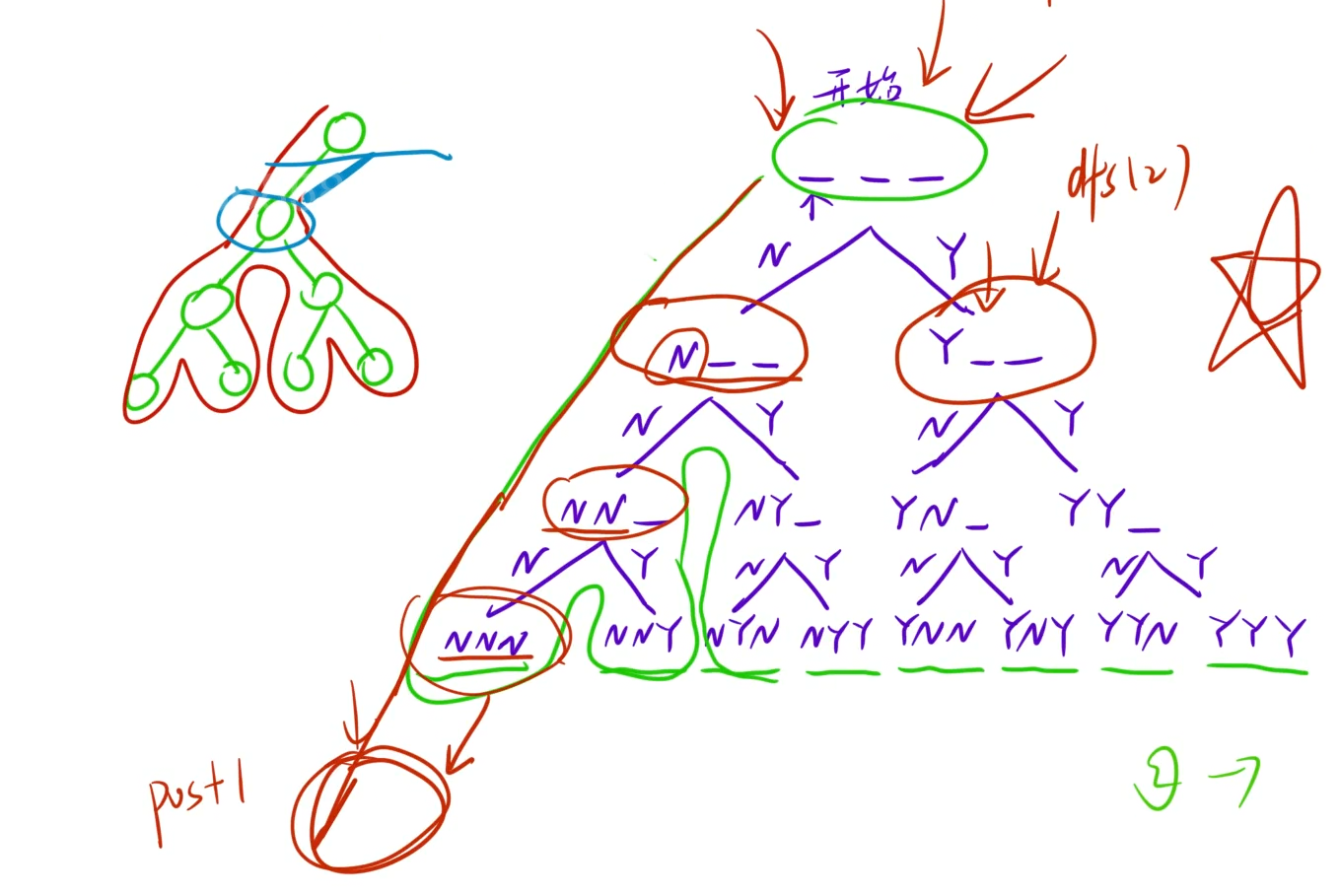
#define  _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;

int n;
string path; //记录递归过程中，每一步的决策

void dfs(int pos)
{
	if (pos > n)
	{
		//path存着前n个人的决策
		cout << path << endl;
		return;
	}

	//不选
	path += "N";
	dfs(pos + 1);
	path.pop_back(); //回溯，清空现场

	//选
	path += "Y";
	dfs(pos + 1);
	path.pop_back();
}

int main()
{
	cin >> n;

	dfs(1);

	return 0;
}

1.2 组合型枚举

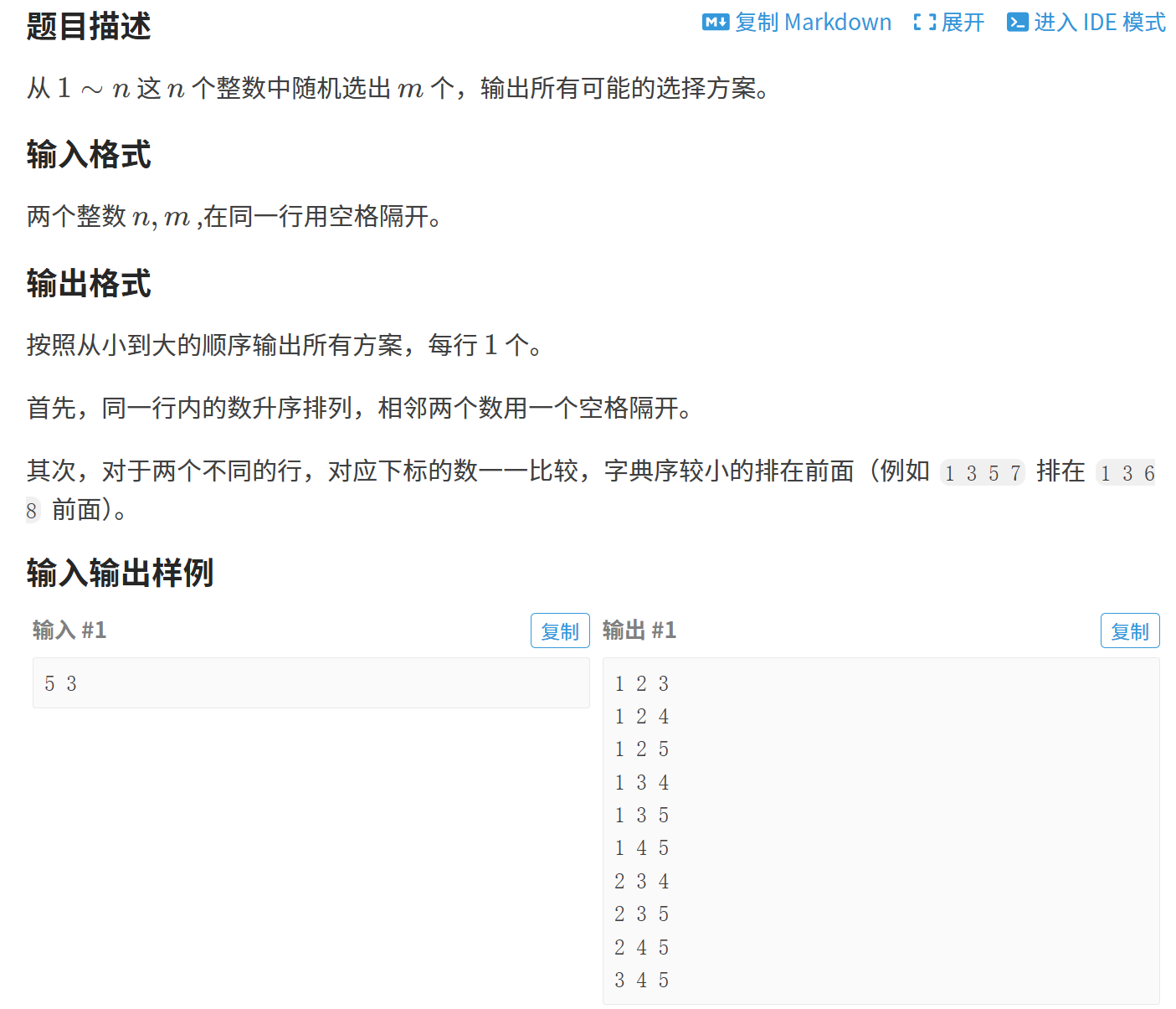
#define  _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <vector>
using namespace std;

int n, m;
vector<int> path;

void dfs(int begin)
{
	if (path.size() == m)
	{
		for (auto e : path)
			cout << e << " ";

		cout << endl;
		return;
	}

	for (int i = begin;i <= n;i++)
	{
		path.push_back(i);
		dfs(i + 1);
		path.pop_back();
	}
}

int main()
{
	cin >> n >> m;

	dfs(1);

	return 0;
}

1.3 枚举排列

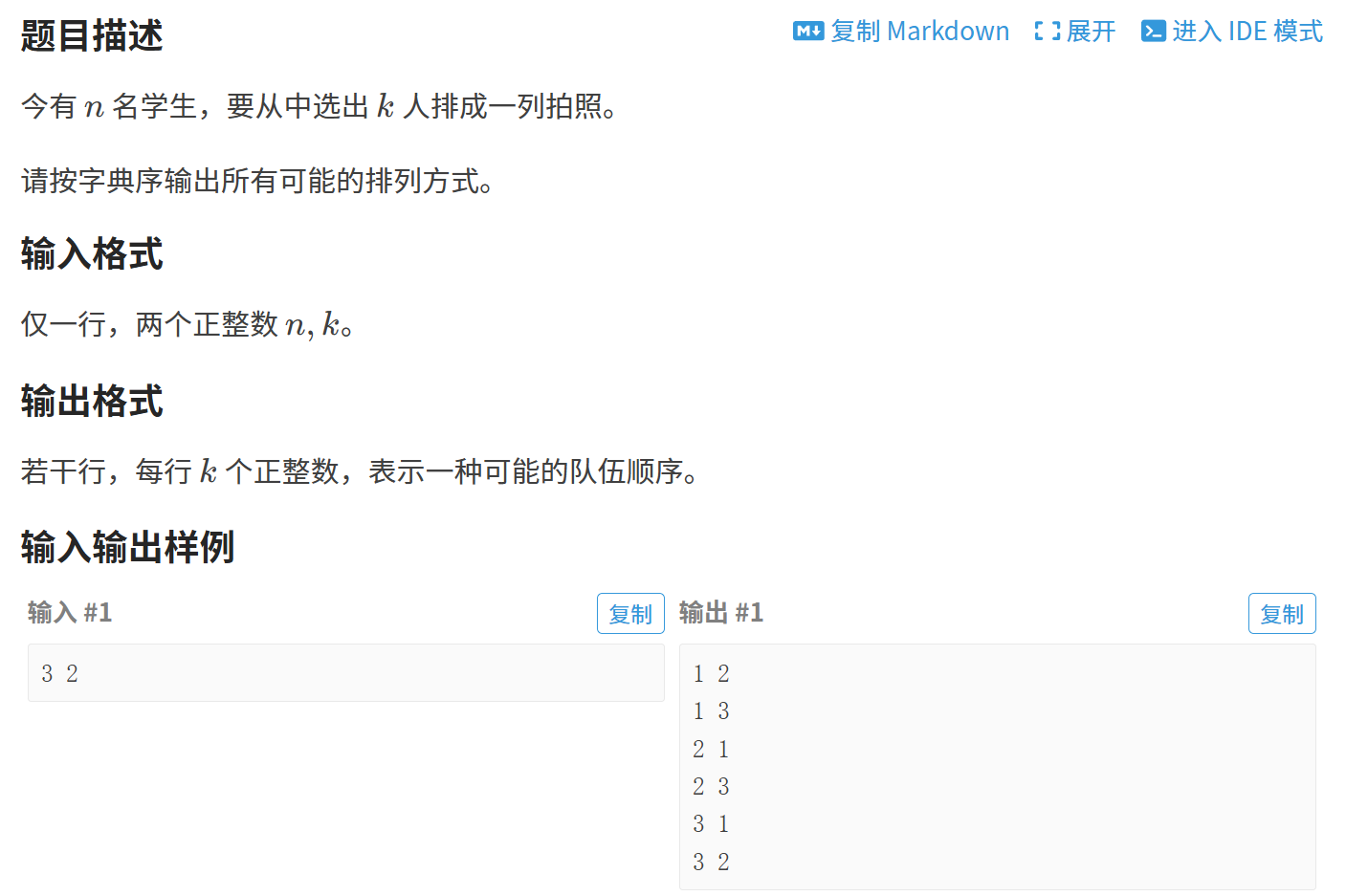
#define  _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <vector>
using namespace std;

int n, k;
vector<int> path;

const int N = 20;
bool st[N];

void dfs()
{
	if (path.size() == k)
	{
		for (auto e : path)
			cout << e << " ";

		cout << endl;
		return;
	}

	for (int i = 1;i <= n;i++)
	{
		if (st[i])
			continue;
		
		path.push_back(i);
		st[i] = true;					
		dfs();

		//恢复现场
		st[i] = false;
		path.pop_back();
	}
}

int main()
{
	cin >> n >> k;

	dfs();

	return 0;
}

1.4 全排列

#define  _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstdlib>
#include <vector>
using namespace std;

int n;
vector<int> path;

const int N = 10;
bool st[N];

void dfs()
{
	if (path.size() == n)
	{
		for (auto e : path)
		{
			printf("%5d", e);
		}
		cout << endl;
		return;
	}
		
	for (int i = 1;i <= n;i++)
	{
		if (st[i])
			continue;

		path.push_back(i);
		st[i] = true;
		dfs();

		path.pop_back();
		st[i] = false;
	}
	
}

int main()
{
	cin >> n;

	dfs();

	return 0;
}