算法基础篇（1）位运算与操作符属性

最新推荐文章于 2025-12-04 22:00:44 发布

原创

最新推荐文章于 2025-12-04 22:00:44 发布 · 771 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#算法

一、原码、反码、补码

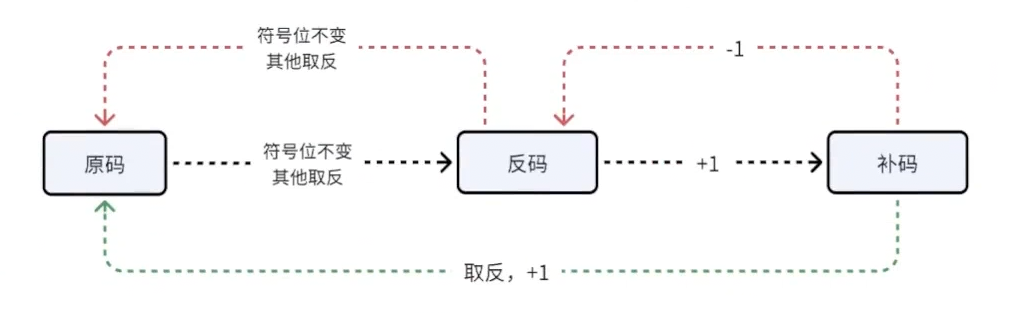
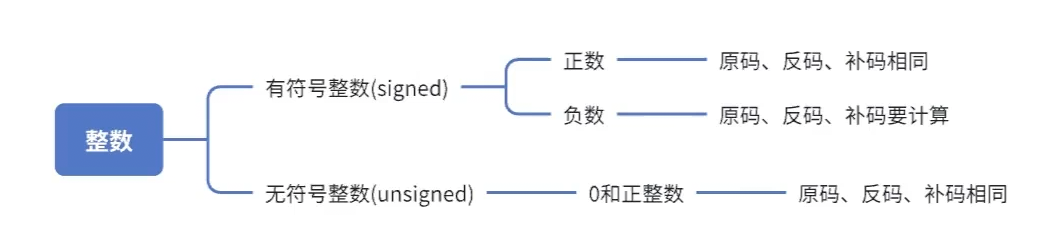
整数的二进制表示方法有三种，分别是原码、反码和补码；整数分为有符号整数（signed）和无符号整数（unsigned）。有符号整数的原码、反码和补码的二进制表示中均由符号位和数值位两部分组成，二进制序列中，最高位的一位是被当做符号位，剩余的都是数值位。符号位都是用0表示“正”，用1表示“负”（如下图所示）。

正整数的原、反、补码都相同

负整数的三种表示方式各不相同，需要计算

原码：直接将数值按照正负数的形式翻译成二进制得到的就是原码。

反码：将原码的符号位不变，其他位依次按位取反就可以得到反码。

补码：反码 + 1 就得到补码。

注：由补码得到原码也可以使用 取反 + 1 的操作。

举个例子：

#include <iostream>
using namespace std;

int main()
{
	int a = 10;
	// 00000000 00000000 00000000 00001010 ---> 原码
	// 00000000 00000000 00000000 00001010 ---> 反码	
	// 00000000 00000000 00000000 00001010 ---> 补码
	
	int b = -10;
	// 10000000 00000000 00000000 00001010 ---> 原码
	// 11111111 11111111 11111111 11110101 ---> 反码
	// 11111111 11111111 11111111 11110110 ---> 补码
		
	return 0;
}

无符号整数三种二进制表示方式相同，没有符号位，每一位都是数值位。

1.1 练习一：十进制转其他进制

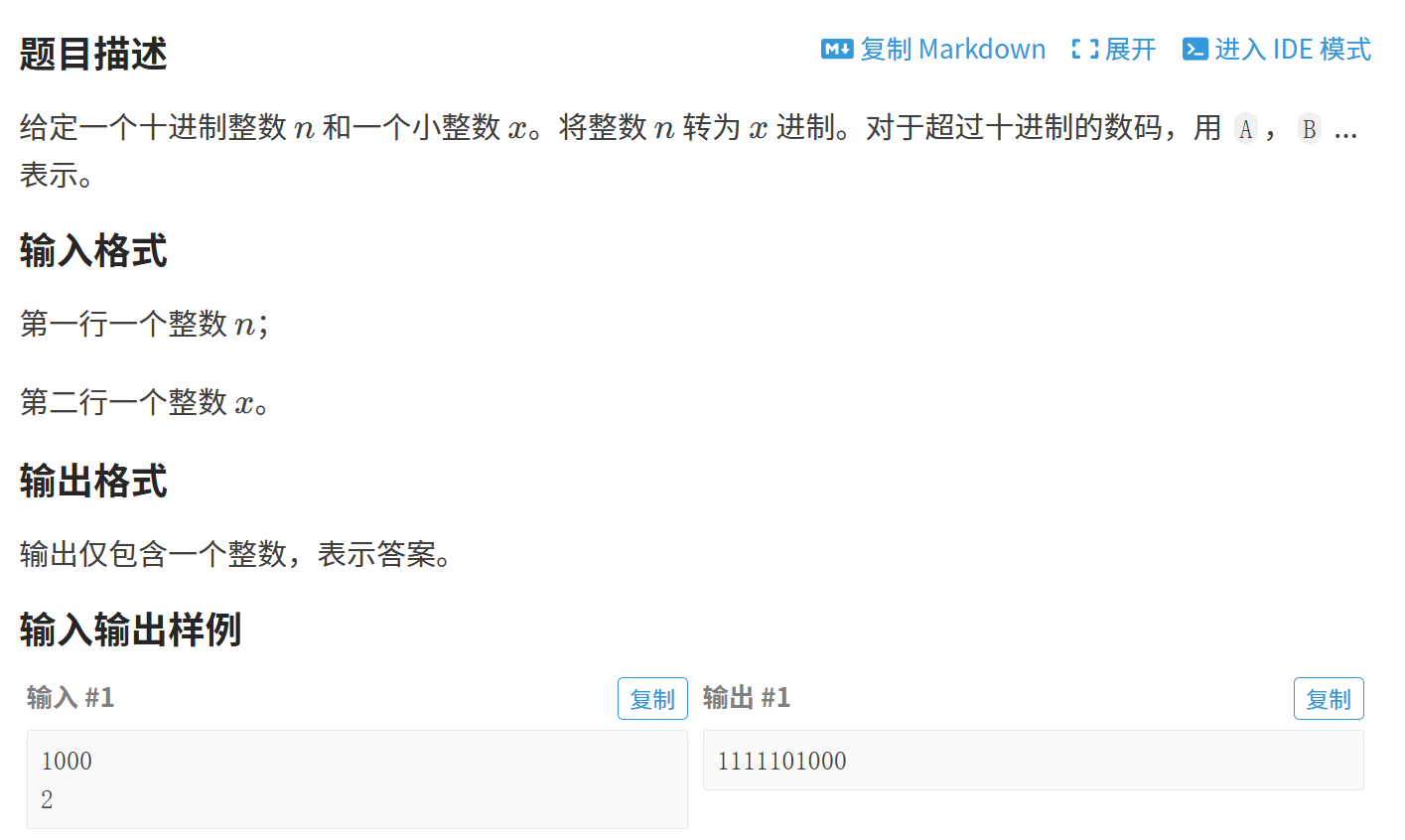
思路分析：我们知道，十进制数字13转换为二进制是1101，最容易得到的就是末尾加红的这个1，直接用 13 % 2 就可以得到。那我们就可以吧 1101 这个二进制序列拆成两部分来看，一半是110，另一半就是末尾的1。而二进制序列110对应的十进制数字是6，那这个6又该怎么得到呢？我们发现13 / 2 得到的值就是6。以此类推，6对应的二进制序列110又可以用刚才的办法得到，所以这道题就可以用递归的思想。

参考代码：

#include <iostream>
using namespace std;

string s = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ";

void n_to_x(int n, int x)
{
	//1
	if(n >= x)
		n_to_x(n / x, x);
	//2
	cout << s[n % x];
}

int main()
{
	int n, x;
	cin >> n >> x;
	n_to_x(n, x);
		
	return 0;
}

1.2 练习二：其他进制转十进制

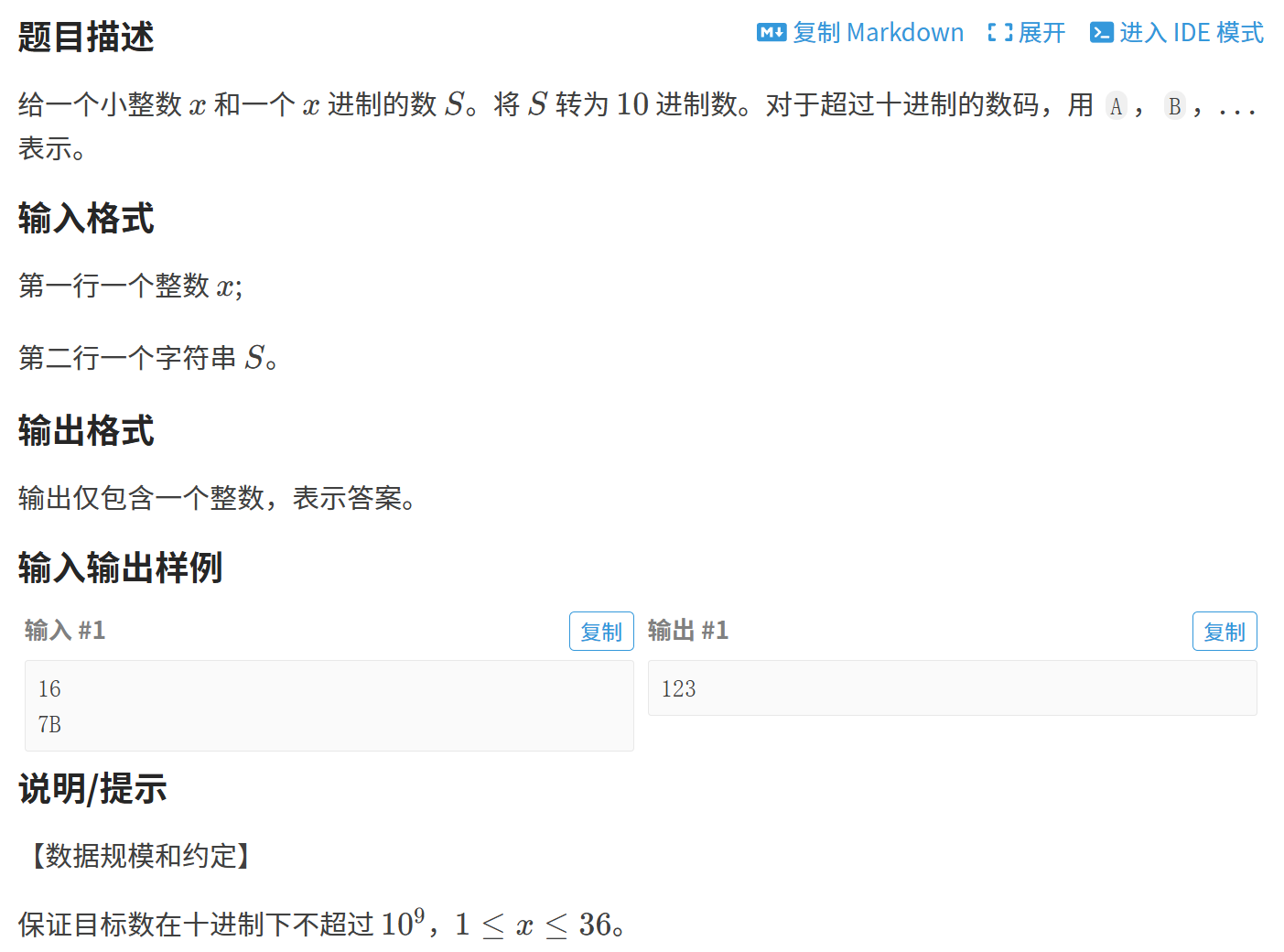
思路分析：像题目中举的这个例子，十六进制的7B该如何转换到十进制对应的数字123呢？其实就是把它的每一位乘上对应的权重就可以得到十进制数字，B × 16^0 == 11，7 × 16^1 == 112，二者相加就得到123。所以，X进制数字转换成10进制的方式就是根据X的每一位乘以自己位的权重，然后求和。

参考代码：

#include <iostream>
#include <string>
#include <cmath>
using namespace std;

// 1.输入x, s
// 2.求出s的长度
// 3.遍历字符串(从后往前遍历), 找出每一个字符转换成整数
//再乘以这一位的权重，最终求和
int main()
{
	int x;
	string s;
	cin >> x >> s;
	int n = s.size() - 1;
	int i = 0;
	int ret = 0;
	while(n >= 0)
	{
		if(s[n] <= '9')
		{
			ret += (s[n] - '0') * pow(x, i);
		}
		else
		{
			ret += (s[n] - 'A' + 10) * pow(x, i);
		}
		n--;
		i++;
	}
	cout << ret << endl;
		
	return 0;
}

当然，这道题还有第二种解法。C++提供了一个函数stoi，用来将字符串转换成int类型的值。