数据结构（15）二叉树算法题

最新推荐文章于 2025-12-02 22:37:42 发布

原创最新推荐文章于 2025-12-02 22:37:42 发布 · 976 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构

C语言篇专栏收录该内容

23 篇文章

订阅专栏

注：本章题目算法思想均采用到了递归，因此前两题算法分析部分只给出了递归流程图

一、单值二叉树

1、题目描述

https://leetcode.cn/problems/univalued-binary-tree

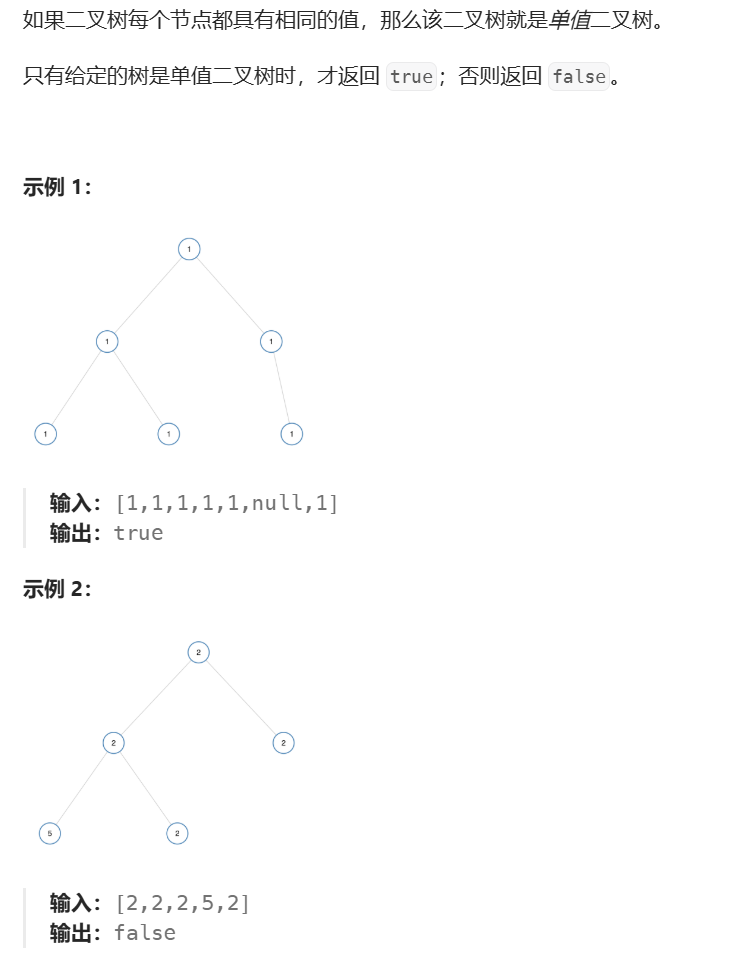
2、算法分析

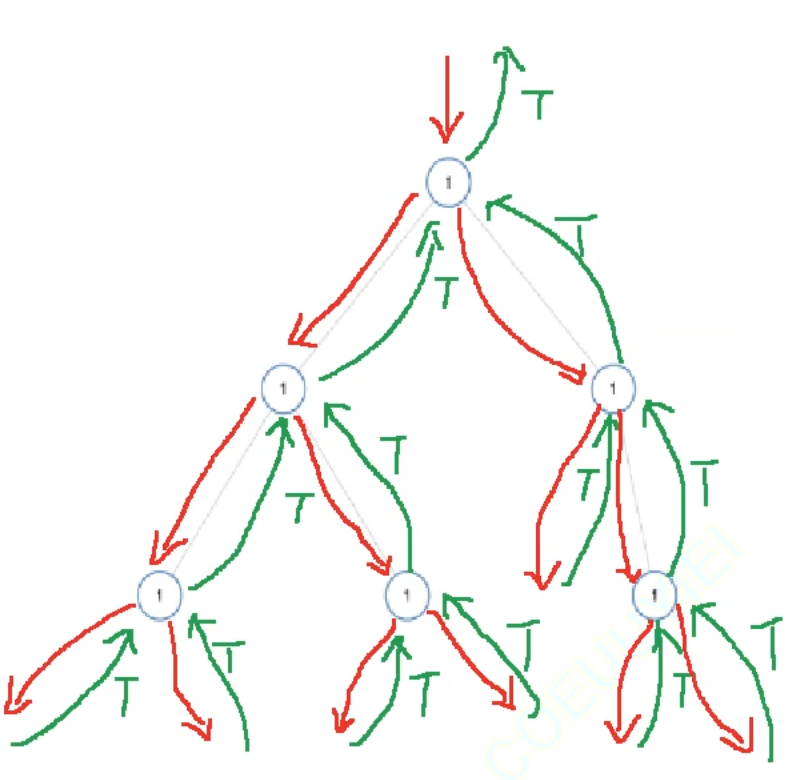
3、参考代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isUnivalTree(struct TreeNode* root) 
{
    if(root == NULL)
    {
        return true;
    }
    if(root->left && root->val != root->left->val)
    {
        return false;
    }
    if(root->right && root->val != root->right->val)
    {
        return false;
    }
    //根结点和左右孩子的值都是相同的
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

二、相同的树

1、题目描述

https://leetcode.cn/problems/same-tree

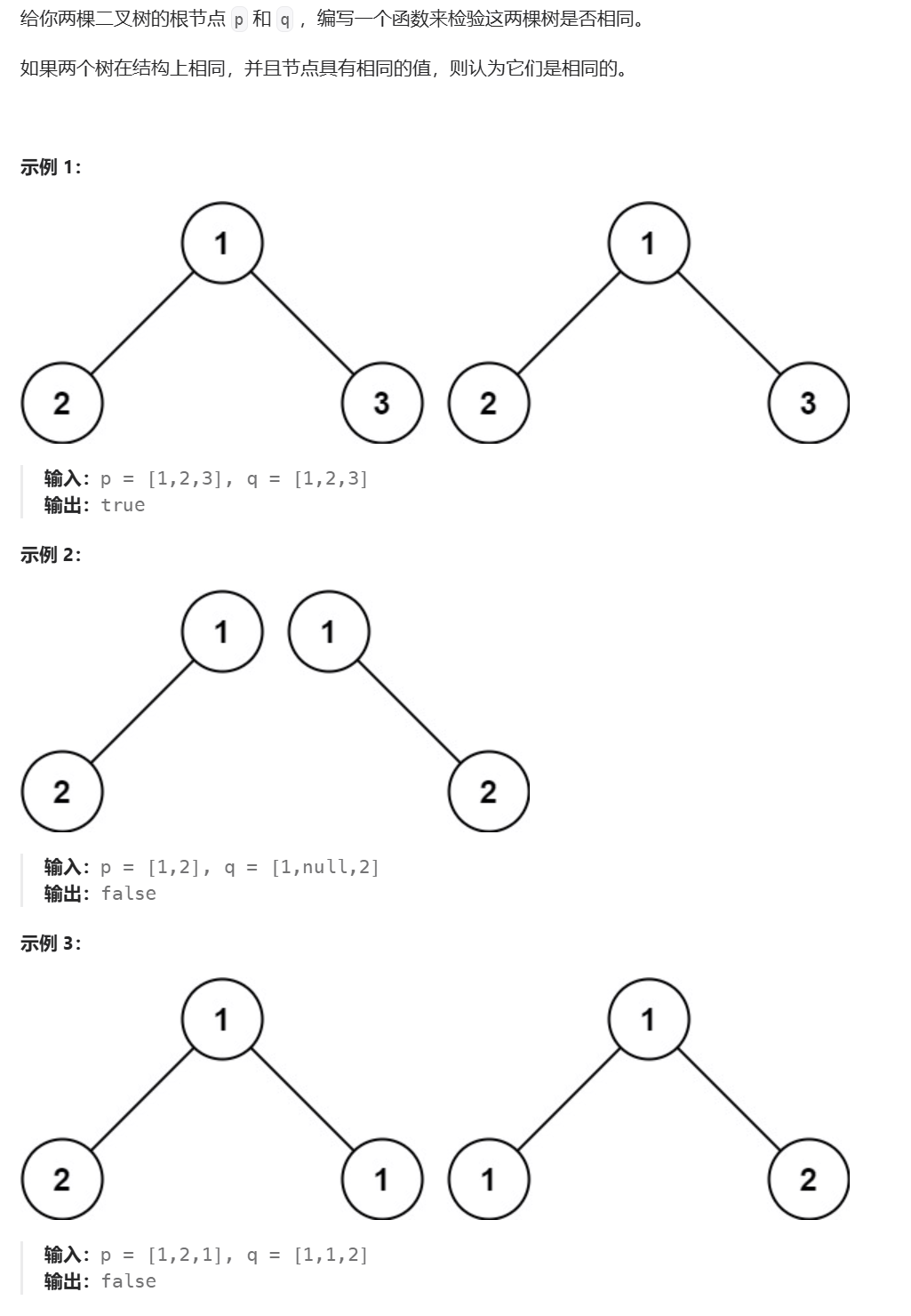
2、算法分析

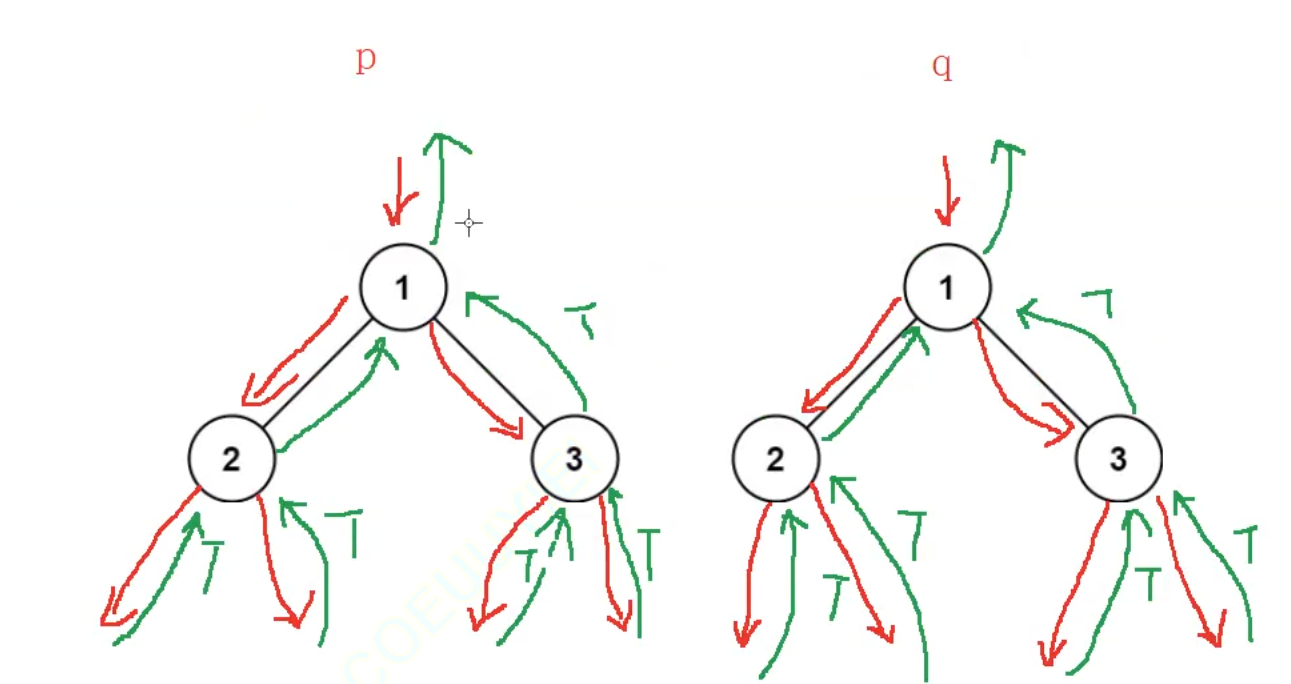
3、参考代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p, struct TreeNode* q) 
{
    //都为空
    if(p == NULL && q == NULL)
    {
        return true;
    }
    //其中一个为空
    if(p == NULL || q == NULL)
    {
        return false;
    }
    //都不为空
    if(p->val != q->val)
    {
        return false;
    }
    //结构相同 + 值相同
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

三、对称二叉树

1、题目描述

https://leetcode.cn/problems/symmetric-tree

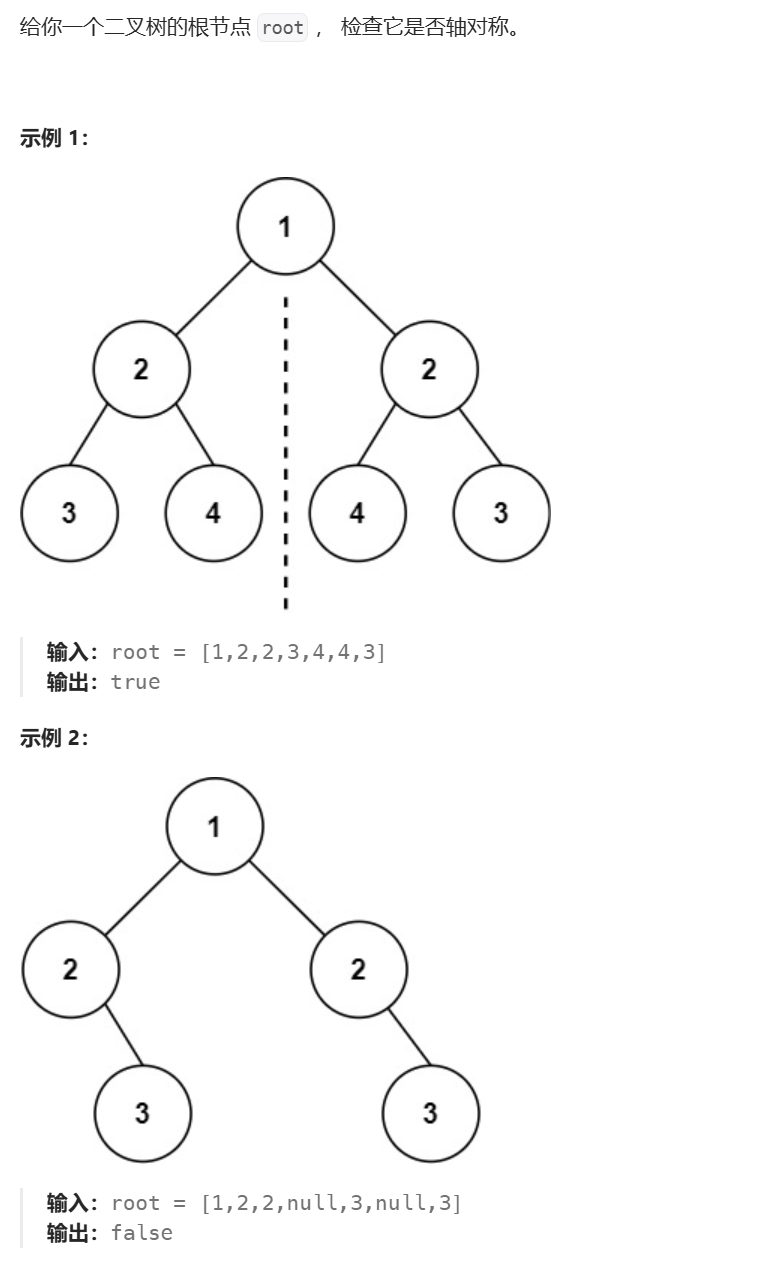
2、算法分析

有了第二题的铺垫，这道题的思路就很简单。那么，这两道题的关系在哪呢？上一道题参数部分提供了两个树的根结点p和q，这道题只提供了一个根结点root。我们把这道题的根结点的左子树看成p，根结点的右子树看成q。然后判断p和q这两棵二叉树是否是相等的。这里要注意一点，这道题判断二叉树是否相同，是要用p的左子树（p->left）和q的右子树（q->right）进行判断，如果相同，再判断p的右子树（p->right）和q的左子树（q->left）是否相同。如果都相同，那我们就能说明p和q是两棵轴对称的二叉树。

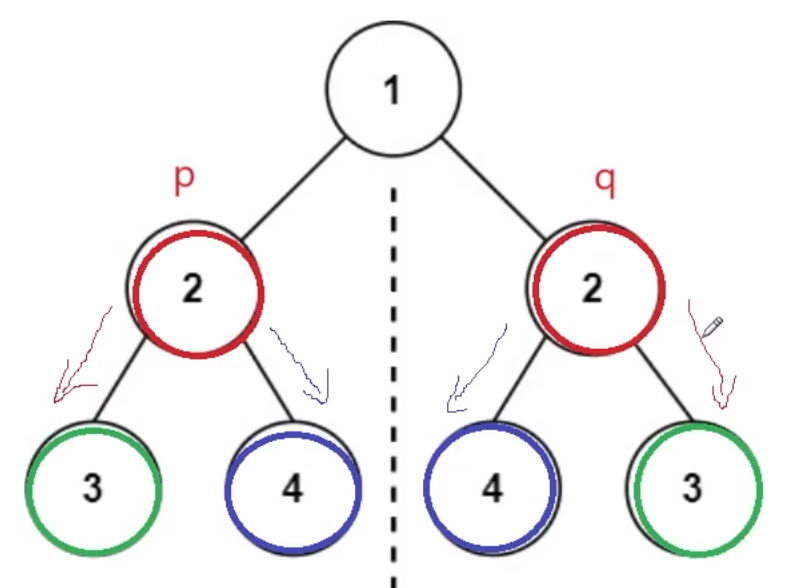
3、参考代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    if(p == NULL && q == NULL)
    {
        return true;
    }
    if(p == NULL || q == NULL)
    {
        return false;
    }
    if(p->val != q->val)
    {
        return false;
    }
    return isSameTree(p->left, q->right) && isSameTree(p->right, q->left);
}
bool isSymmetric(struct TreeNode* root) 
{
    return isSameTree(root->left, root->right);
}

四、另一棵树的子树

1、题目描述

https://leetcode.cn/problems/subtree-of-another-tree

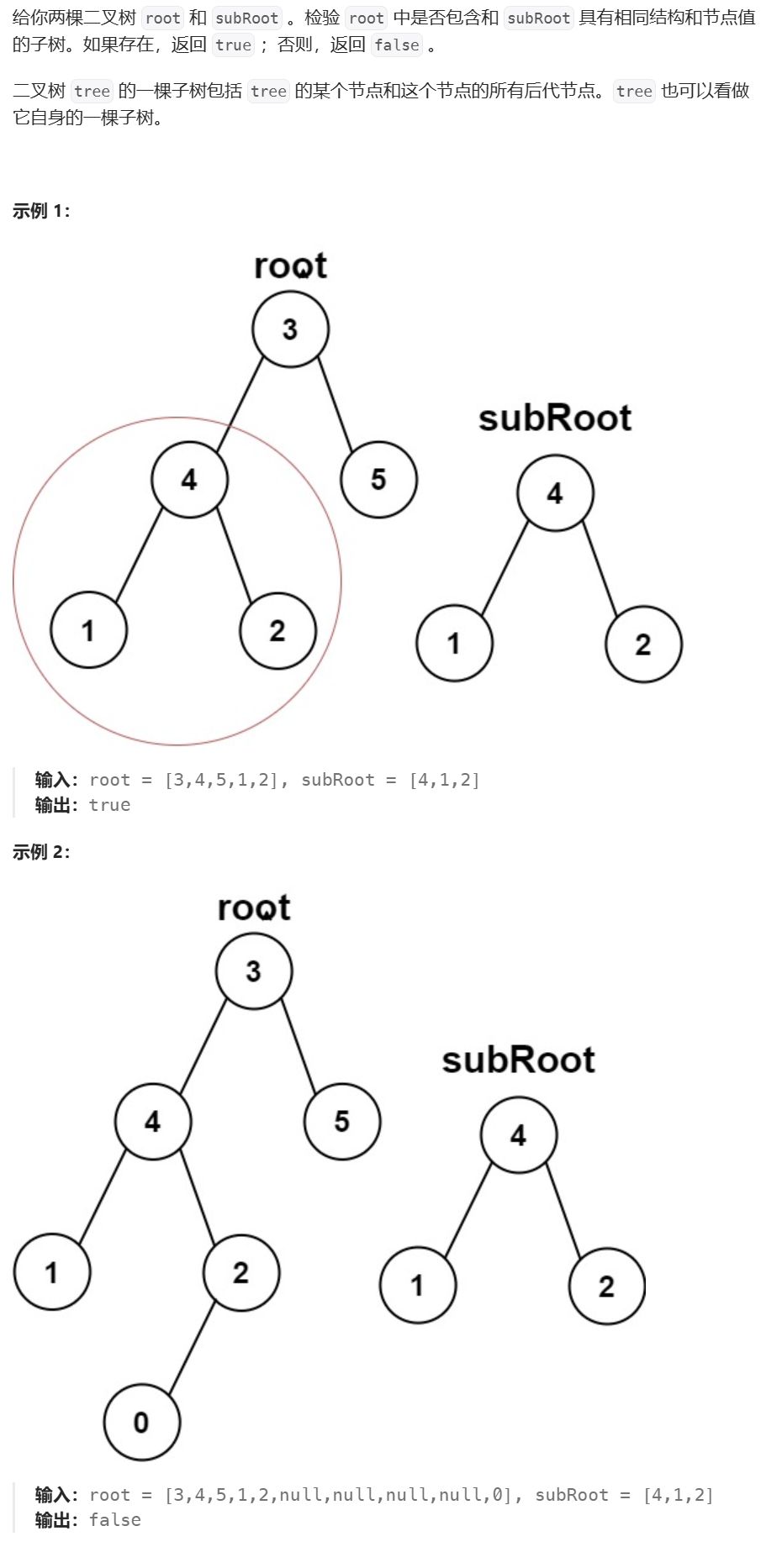
2、算法分析

本题和第二题仍然有相似之处，从根节点出发，判断root和subRoot是否是相同的树，如果不是，继续递归当前二叉树的左子树和subRoot比较，如果不是，就继续递归右子树。

3、参考代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    if(p == NULL && q == NULL)
    {
        return true;
    }
    if(p == NULL || q == NULL)
    {
        return false;
    }
    if(p->val != q->val)
    {
        return false;
    }
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) 
{
    if(root == NULL)
    {
        return false;
    }
    if(isSameTree(root, subRoot))
    {
        return true;
    }
    return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

五、二叉树的前序遍历

1、题目描述

https://leetcode.cn/problems/binary-tree-preorder-traversal

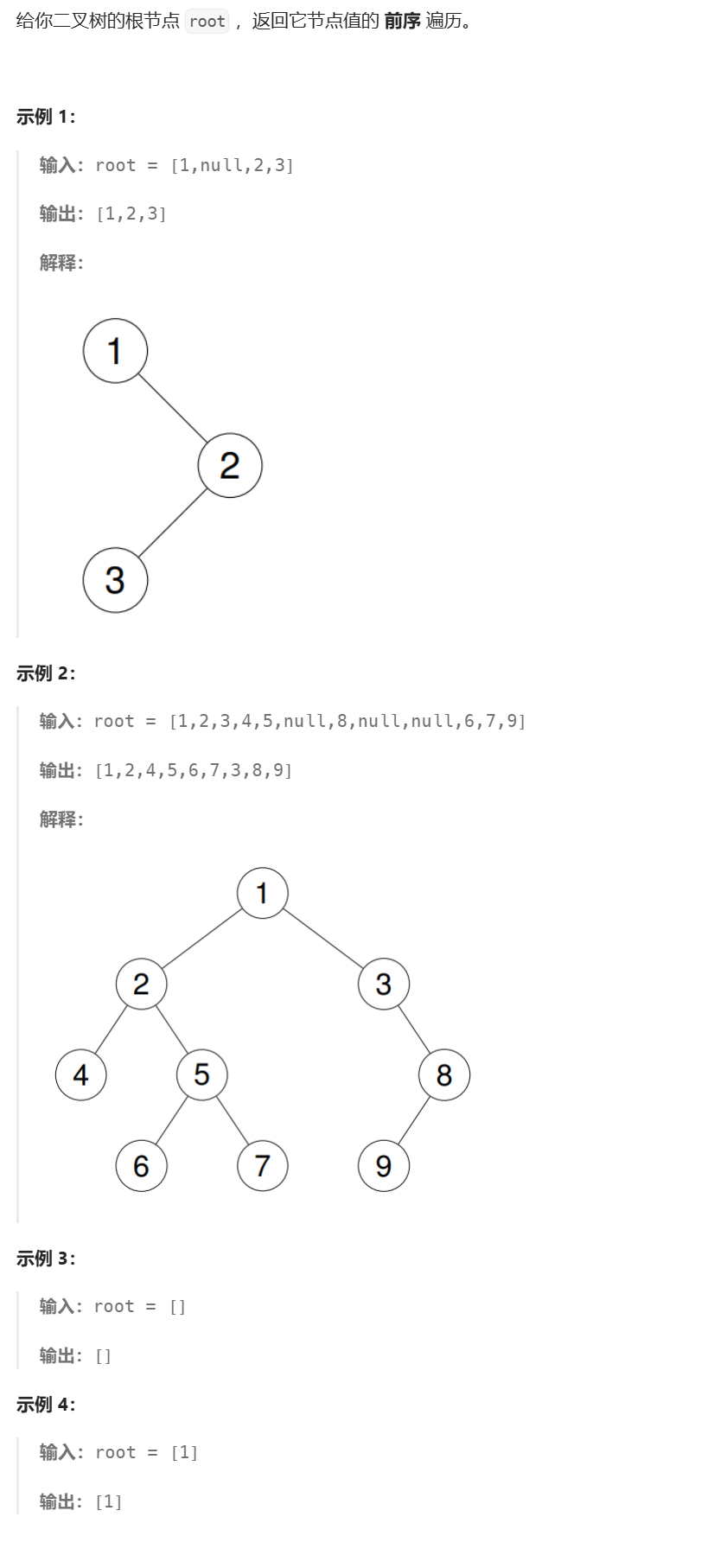
2、算法分析

本题和之前说的前序遍历有所区别，之前所说的前序遍历是直接把结点的值打印出来，而本题是要把结点的值存储到数组里，然后返回该数组的地址。首先是要确定我们需要开辟多大空间的数组，因为数组里存储的是二叉树的结点，所以数组大小取决于结点的个数。第二个问题在于如何把前序遍历的结点的值存储到数组中。注意，我们不能像平常一样定义一个变量i = 0，然后向arr[i]中存储数据，再让i++，原因在上一章也说过了，因为函数栈帧的销毁，形参的改变不影响实参，所以我们要传的是变量i的地址。（具体可以看下面这张图）

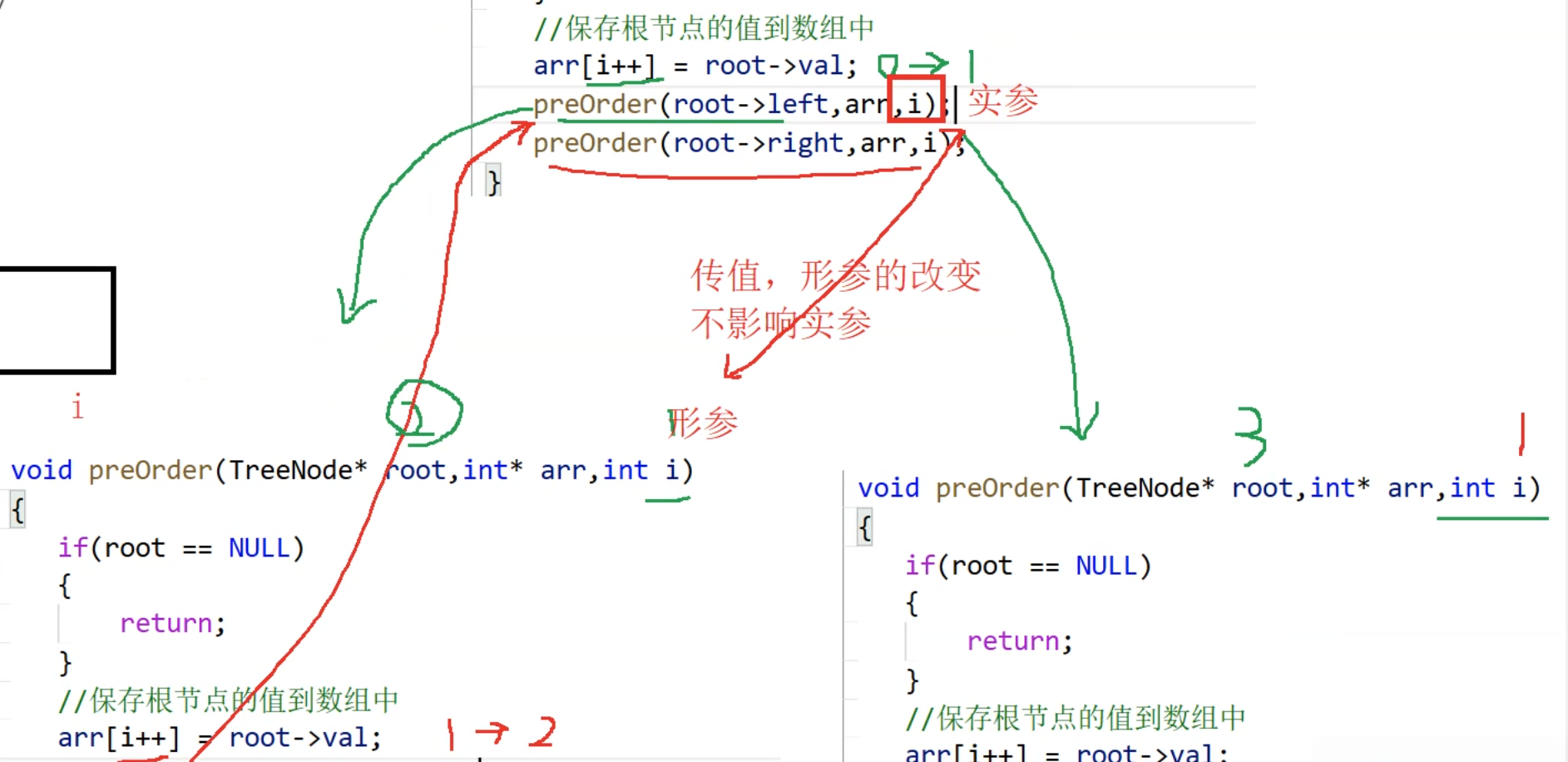
3、参考代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
typedef struct TreeNode TreeNode;
//结点总数 = 1 + 左子树结点个数 + 右子树结点个数
int TreeSize(TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    return 1 + TreeSize(root->left) + TreeSize(root->right);
}
void preOrder(TreeNode* root, int* arr, int* pi)
{
    if(root == NULL)
    {
        return;
    }
    //保存根结点的值到数组中
    arr[*pi] = root->val;
    (*pi)++;
    preOrder(root->left, arr, pi);
    preOrder(root->right, arr, pi);
}
//数组的大小————求二叉树所有节点的个数
int* preorderTraversal(struct TreeNode* root, int* returnSize) 
{
    //求二叉树结点个数
    *returnSize = TreeSize(root);
    //数组要申请*returnSize个int空间
    int* arr = (int*)malloc((*returnSize) * sizeof(int));
    //前序遍历
    int i = 0;
    preOrder(root, arr, &i);

    return arr;
}

六、二叉树的创建与遍历

1、题目描述

2、算法分析

运用递归创建二叉树

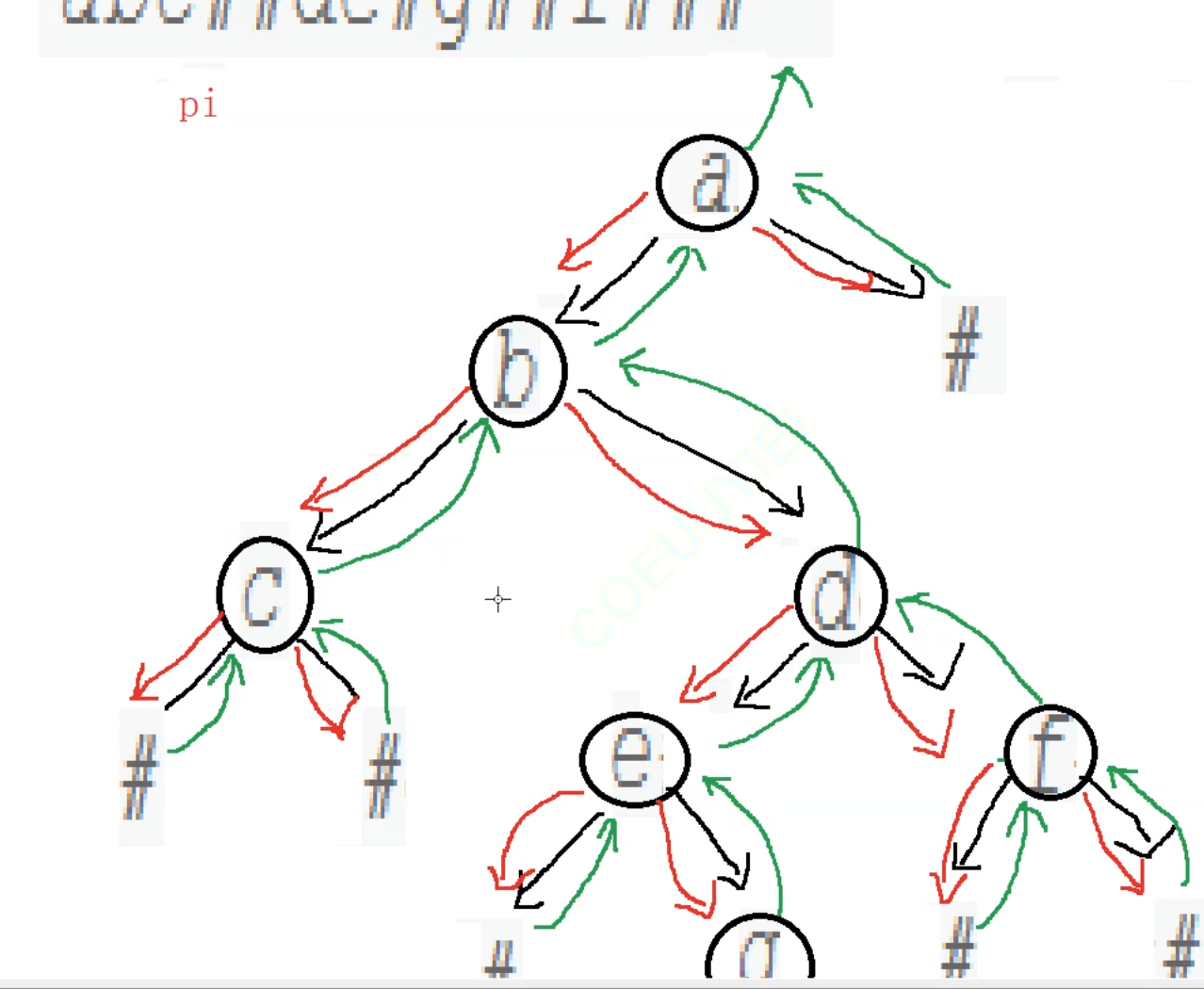
3、参考代码

#include <stdio.h>
#include <stdlib.h>

//二叉树的链式结构
typedef struct TreeNode
{
	char data;
	struct TreeNode* left;
	struct TreeNode* right;
}TreeNode;

TreeNode* buyNode(char ch)
{
	TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));
	if(newNode == NULL)
	{
		perror("malloc fail");
		exit(1);
	}
	newNode->data = ch;
	newNode->left = newNode->right = NULL;
	
	return newNode;
}

TreeNode* createTree(char* arr, int* pi)
{
	if(arr[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}
	TreeNode* root = buyNode(arr[*pi]);
	(*pi)++;
	root->left = createTree(arr, pi);
	root->right = createTree(arr, pi);
	
	return root;
}

void inOrder(TreeNode* root)
{
	if(root == NULL)
	{
		return;
	}
	inOrder(root->left);
	printf("%c ", root->data);
	inOrder(root->right);
}

int main()
{
	//读取输入的前序遍历字符串
	char arr[100];
	scanf("%s", arr);
	//根据前序遍历字符串创建二叉树
	int i = 0;
	TreeNode* root = createTree(arr, &i);
	//二叉树的中序遍历
	inOrder(root);
	
	return 0;
}

———————————————————————————————————————————

二叉树的性质（拓展）

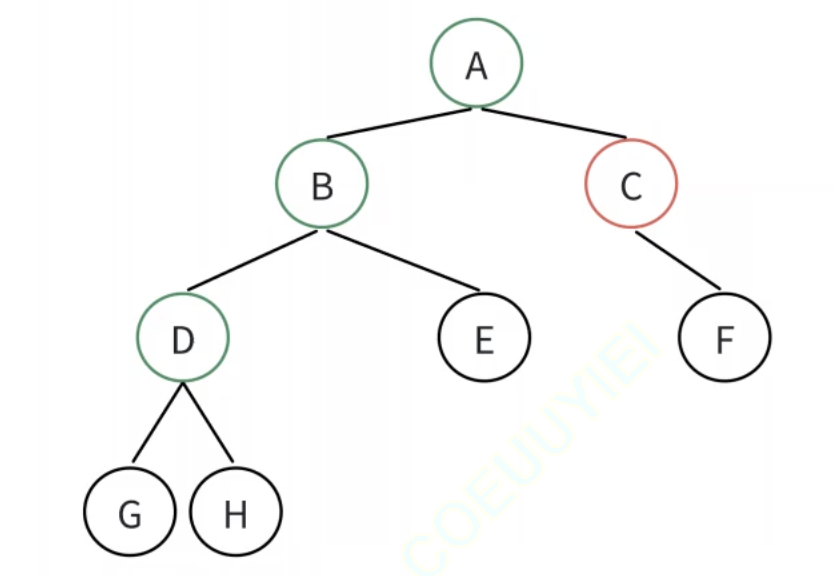
对于任何一棵二叉树，如果度为0（叶子结点）个数为n0，度为2的分支结点个数为n2，则有n0 = n2 + 1

下面给出证明：

假设二叉树度为0的结点个数为n0，度为1的结点个数为n1，度为2的结点个数为n2。那么这棵二叉树的节点总数 n = n0 + n1 + n2，所以二叉树的边数为n - 1，也就是n0 + n1 + n2 -1。又因为度为2的结点边数为2，度为1的结点边数为1，所以边数又可以表示成2 * n2 + n1。

所以 n0 + n1 + n2 - 1 = 2 * n2 + n1，化简得n2 = n0 - 1，得证。