六月GESP

原创已于 2025-08-01 08:47:06 修改 · 置顶 · 417 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #GESP考级

于 2025-07-31 10:56:50 首次发布

GESP 同时被 2 个专栏收录

1 篇文章

订阅专栏

#2025GESP

1 篇文章

订阅专栏

反馈情况

网上经常有人说今年六月二级GESP贼难，出来的人难哭一大片，是真是假？

网上有人传六级比往月要难一些~~（个人感觉简单了一些(^雾^)）~~可我作为一名六级考生，却20分钟做好，40分钟磨洋工，得分96。

一、题目

一、1. 难哭人的二级题目

先看A题

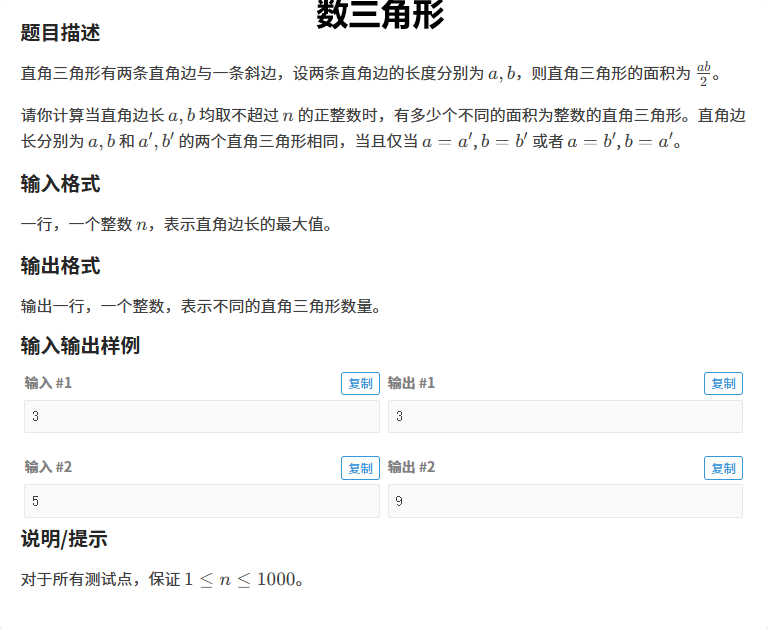
对于我这种在圈子混了几年的高手而言，嵌套for来搞定，判断x为整数就用(int(x)*1.0==x)，

但对于二级的新手宝宝来说，难度适中。

第二道题才是难哭新手宝宝的重点。

如果暴力枚举的话，n有10000种选法，x、y取值在log(10000)以内，暴力要O(N·log(N)·log(N))(N为l、r的最大值。）这么来说，暴力需要19.6ms，可以试试（但在一通加速后只有4ms）。

GESP官方估计怎么也想不到，居然可以暴力。~~二级不本来就靠暴力吗。（雾）~~

但是如果你是大佬，你肯定第一眼就看出来了新做法——二进制编码！看他二进制编码有没有含有2个或1个1。诶！这时候肯定有人要问了，为什么1个1也算呢？4！2！他们只有1个1，但却可以这样拆：4=2^1+2^1、2=2^0+2^0。但要注意一个事情：1它也算了，1顶多拆成2^(-1)+2^(-1)，但因为x、y是非负整数，不能为-1。时间复杂度：O(N·log(N))，只需1.4ms！

哎呀，考生新手宝宝怎么就没想到！有位老师给出了答案——他们太小了不懂什么是幂，因为CSP低龄化，被禁了一大堆，于是这些新手宝宝就到GESP了，谁知遇上最难二级——还有就是考二级的人基本很菜，因为他们一级60~89.5分区间上来的，二级分数自然不会高。

一、2. 简单的六级题目

话不多说，直接上题目。

这道题其实就是一维背包，讨论积极度是价值，第i个数据他的价格就是i。

简直可以称为一坨！

再看第二题。

这题只要学过图论都懂，无非就是一个求质数判断函数改一点为求最大因数，然后RCA就搞定。

二、求解

思路说过了，直接上代码。

新手宝宝别问我下代码有什么用，只是个人习惯，关流（让输出跟输入不要同时进行）加速。

ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);

二、1. 难哭人的二级题目

A、

#include<bits/stdc++.h>
using namespace std;
int n;
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	int cnt=0;
	for(int a=1;a<=n;a++)for(int b=a;b<=n;b++)cnt+=(int((a*1.0*b)/2)*1.0==(a*1.0*b)/2);
	cout<<cnt;
	return 0;
}

B、

暴力（100AC）

#include<bits/stdc++.h>
using namespace std;
int l,r;
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>l>>r;
	int cnt=0;
	for(int n=l;n<=r;n++){
		for(int x2=1;x2<n;x2*=2){
			bool flag=false;
			for(int y2=1;y2+x2<=n;y2*=2)if(x2+y2==n){
				flag=true;
				break;
			}if(flag){
				cnt++;
				break;
			}
		}
	}cout<<cnt;
	return 0;
}

二进制（100AC）

#include<bits/stdc++.h>
using namespace std;
int l,r;
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>l>>r;
	int cnt=0;
	for(int n=max(l,2);n<=r;n++){
		int num=0,tmp=n;
		while(tmp){
			if(tmp%2==1){
				num++;
				if(num==3)break;
			}tmp/=2;
		}if(num<=2)cnt++;
	}cout<<cnt;
	return 0;
}

max(l,2)是为了预防上述1的情况。

二、2. 简单的六级题目

A、

#include<bits/stdc++.h>
using namespace std;
int n,a;
int dp[1010];
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a;
		for(int j=i;j<=n;j++)dp[j]=max(dp[j],dp[j-i]+a);
	}cout<<dp[n];
	return 0;
}

B、

#include<bits/stdc++.h>
using namespace std;
int n,x,y;
map<int,int>dep,father;
int fun(int x){
	if(father[x])return father[x];
	for(int i=2;i*i<=x;i++)if(x%i==0)return father[x]=x/i;
	return father[x]=1;
}
int depf(int x){
	if(dep[x])return dep[x];
	if(x==1)return dep[x]=1;
	return dep[x]=depf(fun(x))+1;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	while(n--){
		cin>>x>>y;
		depf(x);
		depf(y);
		int d=0,u=x,v=y;
		while(dep[u]>dep[v])u=father[u],d++;
		while(dep[v]>dep[u])v=father[v],d++;
		while(u!=v)u=father[u],v=father[v],d+=2;
		cout<<d<<'\n';
	}return 0;
}