蓝桥杯-杨辉三角Ⅱ-力扣

最新推荐文章于 2023-02-27 10:32:45 发布

原创最新推荐文章于 2023-02-27 10:32:45 发布 · 99 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #蓝桥杯 #算法 #idea #java

开发同时被 2 个专栏收录

108 篇文章

订阅专栏

算法

74 篇文章

订阅专栏

本文介绍了一个Java程序来解决杨辉三角的第rowIndex行问题，提供了两种不同的解决方案：递推和线性递推。递推方法通过构建整个三角形逐步计算，而线性递推则直接计算目标行，提高了效率。这两种方法都展示了动态规划的应用。

119. 杨辉三角 II

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。
在「杨辉三角」中，每个数是它左上方和右上方的数的和。

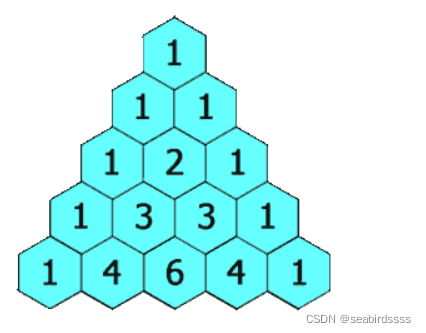
在这里插入图片描述

示例 1:

输入: rowIndex = 3
输出: [1,3,3,1]

示例 2:

输入: rowIndex = 0
输出: [1]

示例 3:

输入: rowIndex = 1
输出: [1,1]

记录题解


import java.util.ArrayList;
import java.util.List;

public class PascalsTriangleIi{
    public static void main(String[] args) {
        Solution solution = new PascalsTriangleIi().new Solution();
        List<Integer> row = solution.getRow(13);
        System.out.println(row);
    }
//leetcode submit region begin(Prohibit modification and deletion)
    class Solution {
        public List<Integer> getRow(int rowIndex) {

            List<List<Integer>> ret = new ArrayList<List<Integer>>();
            for (int i = 0; i < rowIndex+1; ++i) {
                List<Integer> row = new ArrayList<Integer>();
                for (int j = 0; j <= i; ++j) {
                    if (j == 0 || j == i) {
                        row.add(1);
                    } else {
                        row.add(ret.get(i - 1).get(j - 1) + ret.get(i - 1).get(j));
                    }
                }
                ret.add(row);
            }

            return ret.get(rowIndex);
        }
    }
//leetcode submit region end(Prohibit modification and deletion)

}

力扣官方题解

递推

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> row = new ArrayList<Integer>();
        row.add(1);
        for (int i = 1; i <= rowIndex; ++i) {
            row.add(0);
            for (int j = i; j > 0; --j) {
                row.set(j, row.get(j) + row.get(j - 1));
            }
        }
        return row;
    }
}

线性递推

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> row = new ArrayList<Integer>();
        row.add(1);
        for (int i = 1; i <= rowIndex; ++i) {
            row.add((int) ((long) row.get(i - 1) * (rowIndex - i + 1) / i));
        }
        return row;
    }
}