POJ 2187 Beauty Contest (平面最远点对 旋转卡壳)

http://poj.org/problem?id=2187
题意：求平面上点的最远点对间的距离的平方。

平面最近点对是用分治的方法达到$O(nlogn)$的时间复杂度，而平面最远点对是旋转卡壳的应用之一，旋转卡壳的具体说明可参考这篇博客，这里仅写一点我的小小理解。
https://blog.youkuaiyun.com/qq_36172505/article/details/80228394

要求平面最远点对间的距离，显然这两点是位于点集的凸包上的，于是转化成了求凸多边形的直径的问题，凸多边形的直径是由凸多边形的对踵点(即平面最远点对)决定的，要在$O(n)$时间复杂度内完成就要用到旋转卡壳了。
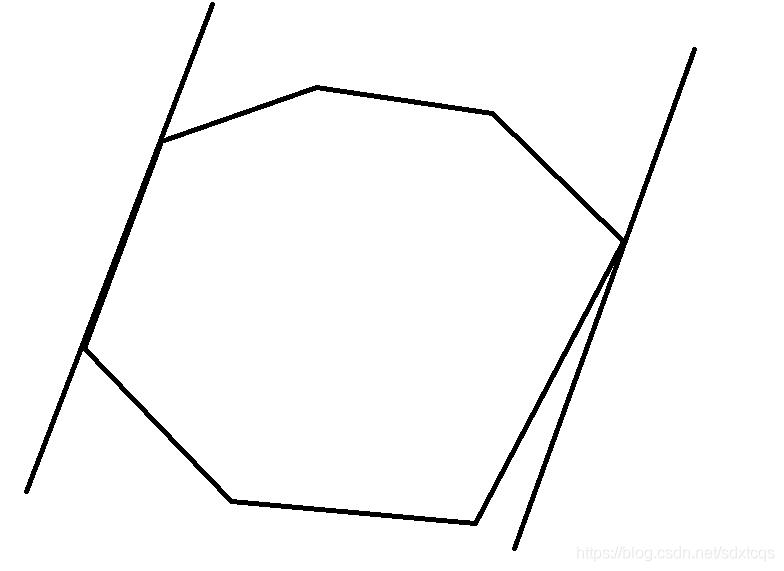
旋转卡壳的原理也不难，对踵点可以理解成凸多边形被两条平行的直线卡住，要这两条直线间的距离最大，此时卡住的两个点就是对踵点。而卡住的情况有两种，第一种是卡住了两个点，第二种是卡住了一个点和其对边，当然其实这两种情况是相通的。在第二种情况中，我们可以看到，对踵点的一个点和对应边之间的距离比其他点到那条边的距离要大，也就是一个对踵点和对应边所形成的三角形面积是最大的。
如果A，B是对踵点，必然可以分别过A，B画出一对平行线。通过旋转这对平行线，我们可以让它和凸包上的一条边重合，可以注意到，A是凸包上离P和B所在直线最远的点。于是我们的思路就是枚举凸包上的所有边，对每一条边找出凸包上离该边最远的顶点，计算这个顶点到该边两个端点的距离，并记录最大的值。直观上这是一个$O(n^2)$的算法，和直接枚举任意两个顶点一样了。
然而我们可以发现，凸包上的点依次与对应边产生的距离成单峰函数，利用这个关键的单调性我们就可以将时间复杂度优化到$O(n)$了，写起来也很简单，逆时针枚举边的同时，逆时针枚举点，而利用单峰性，不需要从头枚举对应点，而是接着上次枚举到的点继续枚举即可。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cmath>
using namespace std;
struct Point
{
	int x,y;
	Point(){}
	Point(int _x,int _y)
	{
		x=_x;y=_y;
	}
	Point operator -(const Point &b)const
	{
		return Point(x-b.x,y-b.y);
	}
	int operator ^(const Point &b)const
	{
		return x*b.y-y*b.x;
	}
	int operator *(const Point &b) const
	{
		return x*b.x+y*b.y;
	}
	void input()
	{
		scanf("%d%d",&x,&y);
	}
};
//距离的平方
int dist2(Point a,Point b)
{
	return (a-b)*(a-b);
}
//二维凸包(int)
const int MAXN=50010;
Point list[MAXN];
int Stack[MAXN],top;
//相对于list[0]进行极角排序
bool _cmp(Point p1,Point p2)
{
	double tmp=(p1-list[0])^(p2-list[0]);
	if(tmp>0)
		return true;
	else if(tmp==0&&dist2(p1,list[0])<=dist2(p2,list[0]))
		return true;
	else return false;
}
void Graham(int n)
{
	Point p0;
	int k=0;
	p0=list[0];
	//找最左下的点
	for(int i=1;i<n;i++)
	{
		if((p0.y>list[i].y)||(p0.y==list[i].y&&p0.x>list[i].x))
		{
			p0=list[i];
			k=i;
		}
	}
	swap(list[k],list[0]);
	sort(list+1,list+n,_cmp);
	if(n==1)
	{
		top=1;
		Stack[0]=0;
		return ;
	}
	if(n==2)
	{
		top=2;
		Stack[0]=0;
		Stack[1]=1;
		return ;
	}
	Stack[0]=0;
	Stack[1]=1;
	top=2;
	for(int i=2;i<n;i++)
	{
		while(top>1&&((list[Stack[top-1]]-list[Stack[top-2]])^(list[i]-list[Stack[top-2]]))<=0)
			top--;
		Stack[top++]=i;
	}
}
//旋转卡壳，求两点间距离的平方的最大值
int rotating_calipers(Point p[],int n)
{
	int ans=0;
	Point v;
	int cur=1;
	for(int i=0;i<n;i++)
	{
		v=p[i]-p[(i+1)%n];
		while((v^(p[(cur+1)%n]-p[cur]))<0)
			cur=(cur+1)%n;
		ans=max(ans,max(dist2(p[i],p[cur]),dist2(p[(i+1)%n],p[(cur+1)%n])));
	}
	return ans;
}
Point p[MAXN];
int main()
{
	int n;
	scanf("%d",&n);
	for(int i=0;i<n;i++)
		 list[i].input();
	Graham(n);
	for(int i=0;i<top;i++)
		p[i]=list[Stack[i]];
	printf("%d\n",rotating_calipers(p,top));
	return 0;
}