置换群定理 Pólya定理：

最新推荐文章于 2019-01-04 08:22:00 发布

原创最新推荐文章于 2019-01-04 08:22:00 发布 · 649 阅读

0 ·

CC 4.0 BY-SA版权

模板专栏收录该内容

69 篇文章

订阅专栏

本文探讨了Pólya定理在置换群理论中的应用，通过一个具体的编程实例，展示了如何利用该定理计算用不同颜色染色的方案数。在置换群G中，通过对置换ak的循环节进行分析，可以有效地计算出m种颜色染色的n个对象的不同方案数量。

Pólya定理：

在一个置换群G={a1,a2,a3……ak}中，设C(ak)是在置换ak的循环节个数，那么用m种颜色染图这n个对象，则不同的染色方案数为：


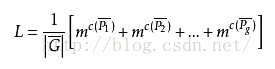
int main()
{
    //用c种颜色给有n*n的格子的墙染色 用m墙围成房子 问不同的房子多少种    
    ll n,m,c,i,ans = 0,x;
    scanf("%lld%lld%lld",&n,&m,&c);

    for(i=0;i<m;i++)
    {
        x = __gcd(i,m);
        ans += pow_mod(c,n*n*x);
        ans %= mod;
    }
    ans = ans * pow_mod(m,mod-2)%mod;
    printf("%lld\n",ans);
    return 0;
}