GBDT用负梯度代替残差的推导

今天在B站看了GDBT的入门；GBDT模型是一个集成模型，是很多CART树的线性相加。
GBDT模型可以表示为以下形式，我们约定f­­­t­(x)表示第t轮的模型，ht(x)表示第t颗决策树，模型定义如下：

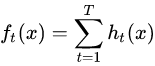
提升树采用前向分步算法。第t步的模型由第t-1步的模型形成，可以写成：

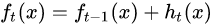
损失函数自然定义为这样的：

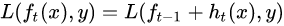
对于一般的回归树，采用平方误差损失函数，这时根据前向分布每次只需要达到最优化，就能保证整体上的优化。由于平方误差的特殊性，可以推导出每次只需要拟合残差（真实值-预测值）。而对于其他损失函数， Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值，进而拟合一个CART回归树。即每次需要拟合的是模型的负梯度：

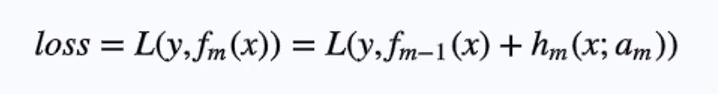
公式不太好打，偷个小懒，然后这里的m就是前面的t，αm就是第m根树的参数。按照泰勒对损失函数求f(x)(m-1)（这里的m-1表示下标）的一节展开式如下：

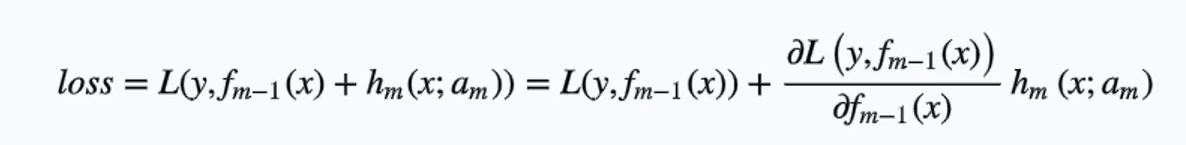
就是这个地方的泰勒展开式把我整懵了，并且我看弹幕里面有几个小伙伴也是一脸懵逼，所以以为是什么高深的东西，还在百度找了半天，后来发现竟然没有人说这个东西！然后就开始怀疑自己，是不是这是很基础的东西，只是因为自己忘记了所以。。。
事实证明，确实如此，这里只是泰勒公式的一个形式而已 ：

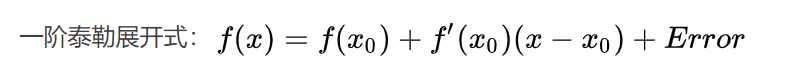
然后泰勒公式里面的x就相当于损失函数里的（y，f(x)(m-1)），泰勒公式里面的x0就相当于h(x，αm)_m，其实是很简单的公式，但是太久没用了，记录一下，嘻嘻。
另外多说一句，我们在理解上述损失函数的泰勒展开式的时候先不用管y，只看x这个维度就好，会容易理解一些。