梯度下降算法

• 梯度下降法 Gradient descent
  
  作用： 用来最小化函数，这里用来最小化代价函数。
  做法是：给定a,b最初值，一般起初都为0，然后不停的一点点（在图像上表示即是360度环绕四周，我下一步要怎么走才能最快下降到山底）的改变a,b来使得代价函数变小，直到找到代价函数的最小值或者局部最小值。从而也就确定了a,b的值
  梯度下降法的特点：最初点选择不同会得到一个不同的最优解。
  简化研究：假设只有一个参数如下图
  

如果梯度下降已经到达了一个局部最优解，那么下一步梯度下降会怎么样？
答：参数将不再改变，如下图解释

• 常存在局部最优解的问题，选择不同的初始值，最后得到的最优解可能不同
• 

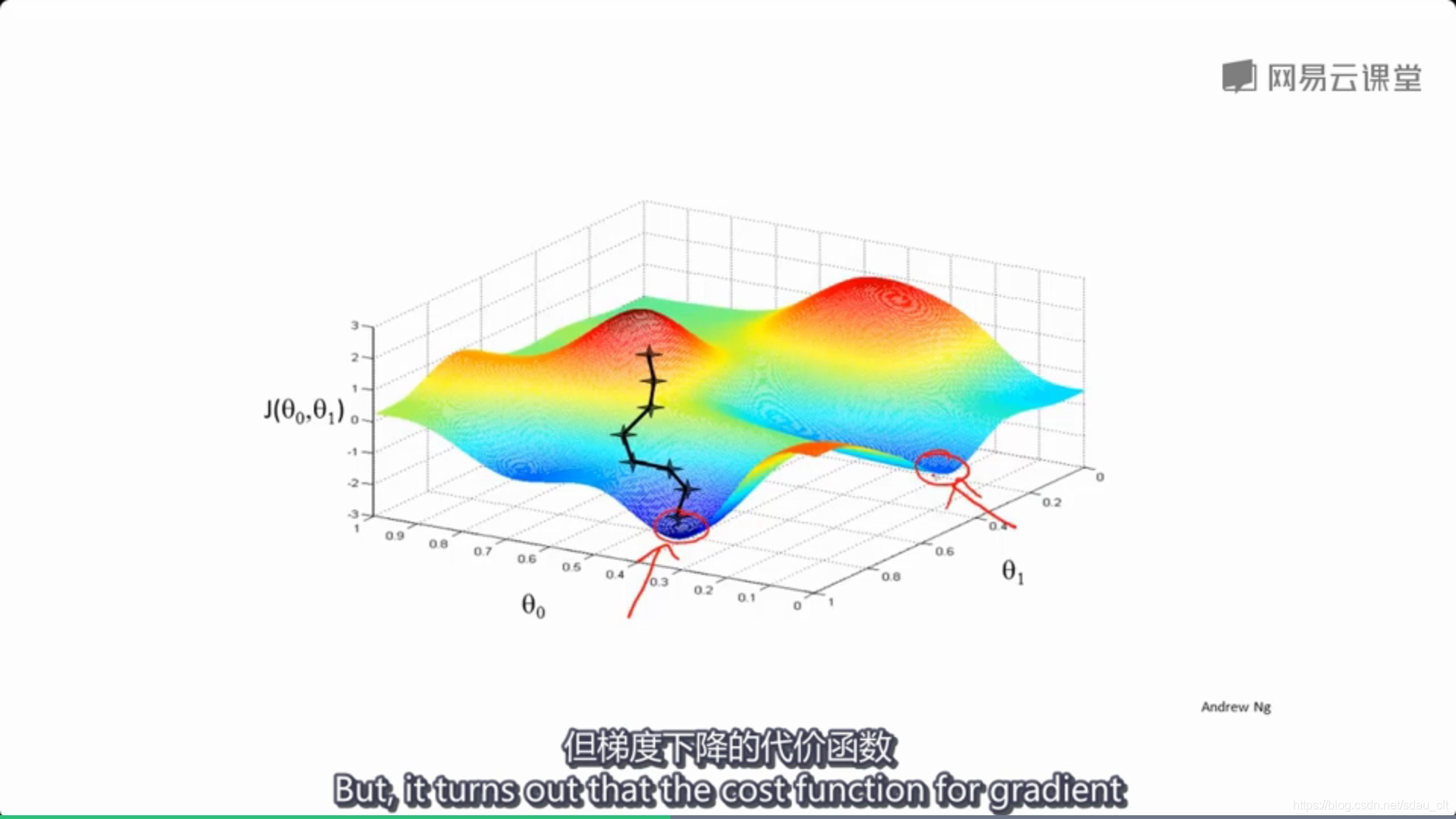
多元梯度下降法

将梯度下降算法应用到多元线性回归中

梯度下降算法中的实用技巧

特征缩放
如果能够确保多个特征值得取值范围相近，会使得梯度下降算法收敛的更快。

关于特征缩放和均值归一化，详见这篇博客，博主总结很全
学习率，如何选择学习率
画出迭代曲线有助于我们判断是否梯度下降正常工作和是否已经收敛

• 当曲线出现下边三种情况时，我们的解决办法是选择更小的学习率
• 
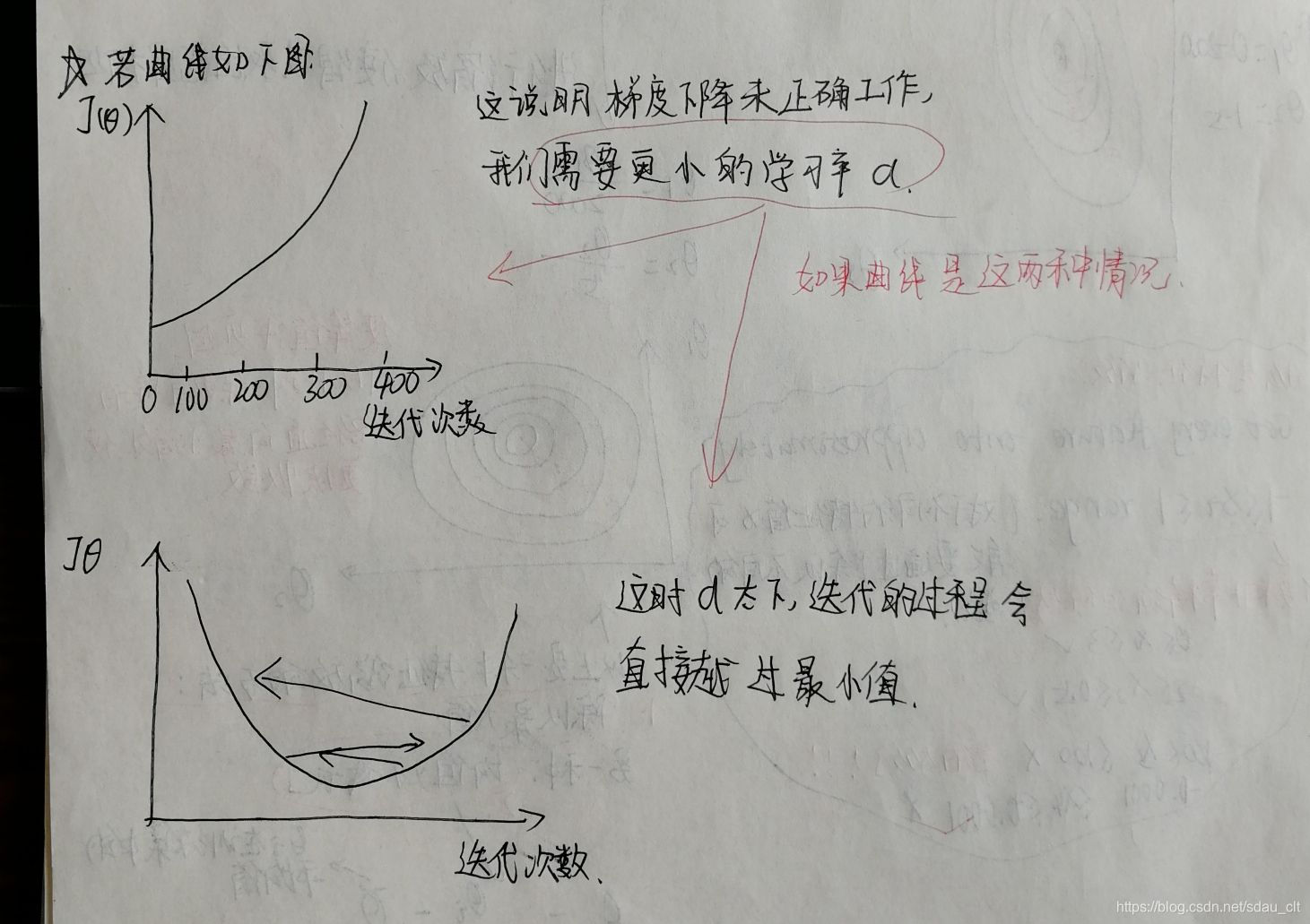
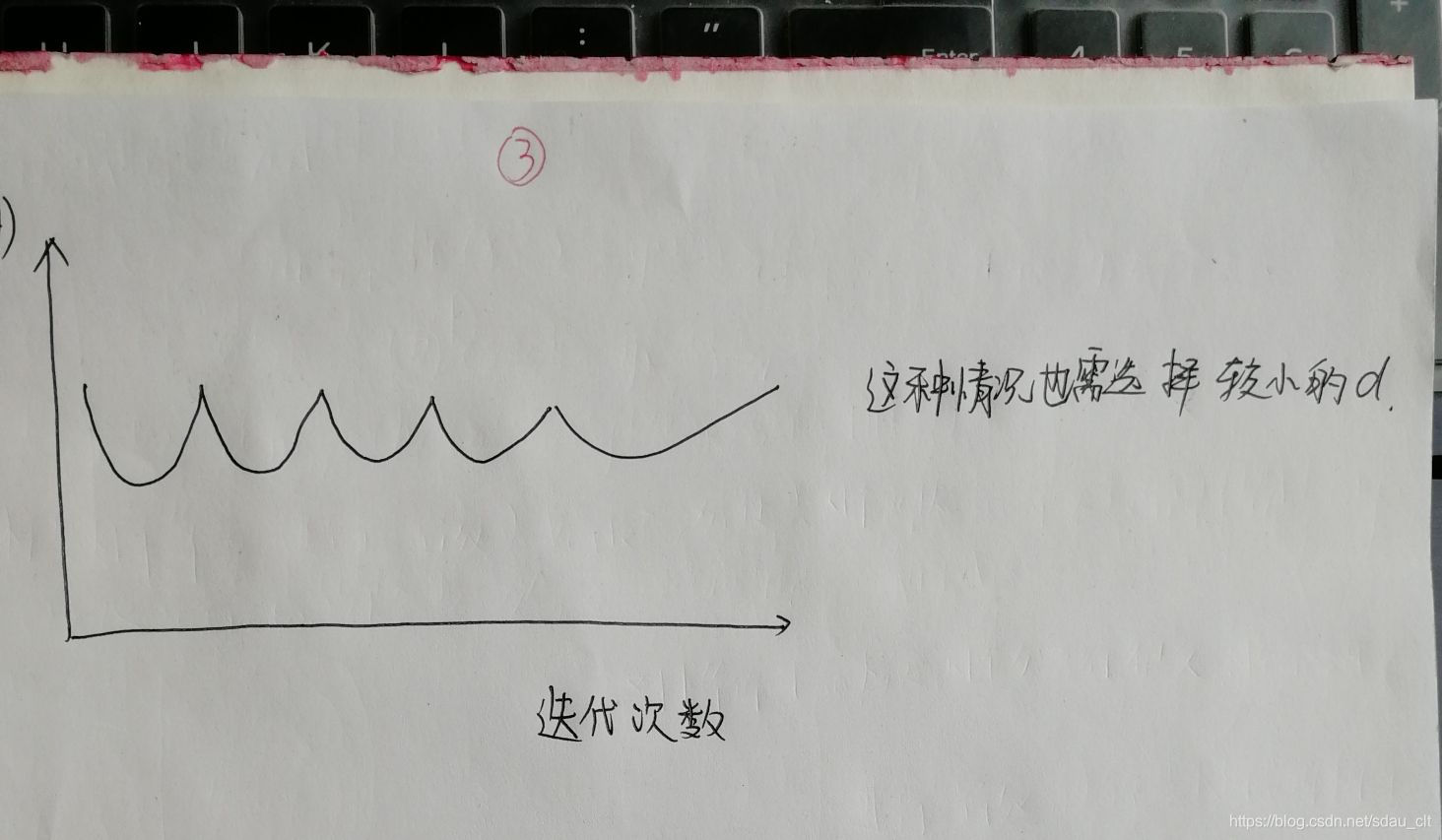
• 学习率太大会出现的问题总结
  代价函数可能不是在每一次迭代都下降，也可能会不收敛，也可能迭代的非常慢

数学家已经证明，如果学习率足够小那么每次迭代都会使得代价函数变小，当然学习率也不能太小，太小的话会收敛的非常慢。

• 经验
  在运行梯度下降算法时，尝试多个学习率，0.001, 0.003，0.01, 0.03， 0.1, 0.3 ，1等，回执迭代步数变化的曲线，选择使得代价函数快速下降的学习率值