AtCoder Beginner Contest 295（DEG）

最新推荐文章于 2023-10-14 17:11:49 发布

原创最新推荐文章于 2023-10-14 17:11:49 发布 · 504 阅读

0 ·

CC 4.0 BY-SA版权

kkk

文章标签：

#哈希算法 #算法 #c++

文章介绍了三道编程竞赛题目，包括D-ThreeDaysAgo、E-KthNumber和G-MinimumReachableCity。D题通过前缀和解决奇偶性问题，E题计算给定条件下数列中数字的期望值，G题利用并查集处理图的连通性和查询问题。每道题都给出了思路和代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

D - Three Days Ago (atcoder.jp)

（1）题目大意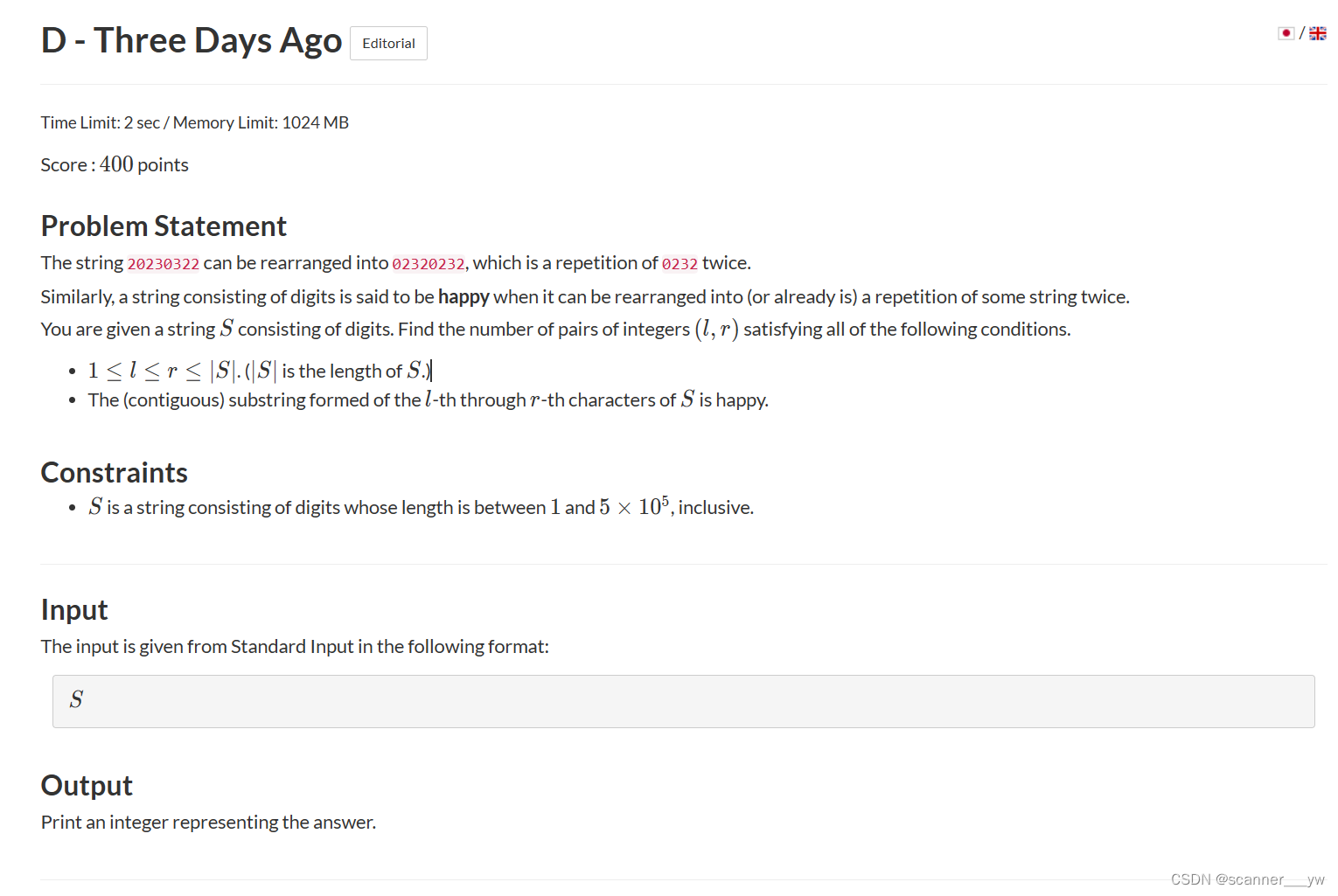

（2）解题思路

考虑使用前缀和的思路，把每一个位置0-9的数量的奇偶表示出来，用一个map或者hash维护一下即可，每一次找到和当前奇偶相同的位置就是答案。

（3）代码实现

#include <iostream>
#include <map>
#include <set>
#include <vector>
#include <cstring>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <cmath>
#include <unordered_map>
#include <deque>
#include <bitset>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
int cnt[10];
void solve()
{
    map <vector<int>,int> mp;
    string s;
    cin >> s;
    ll ans = 0;

    vector <int> v;
    rep(j,0,9) v.pb(0);
    mp[v] ++; 
    for(int i = 0;i < sz(s);i ++) {
        v.clear();
        cnt[s[i] - '0'] ++;
        rep(j,0,9) v.pb(cnt[j] & 1);
        ans += mp[v];
        mp[v] ++;
    }
    cout << ans << endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}

E - Kth Number (atcoder.jp)

（1）题目大意

给你N个数里面有0或者其他，你可以把其中的0替换成其他的数，问你第k个数的期望是多少。

（2）解题思路

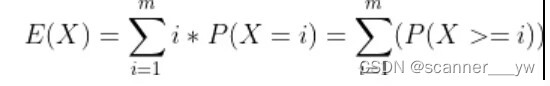
把式子转换一下，然后枚举把第k个位置变为i的期望，等价与有n-k+1个大于>=i的位置，然后算一下选多少个小于等于i的数和多少个大于等于i的数，通过组合数算出来，然后把这些期望相加即可。

（3）代码实现

#include "bits/stdc++.h"

using namespace std;
using ll = long long;
using i64 = long long;
constexpr int P = 998244353;
constexpr int N = 1e6 + 5;
ll ksm(ll a,ll b)
{
    ll res = 1;
    a %= P;
    while(b) {
        if(b & 1) res = res * a % P;
        a = a * a % P;
        b >>= 1;
    }
    return res;
}
struct Combination {
    ll fac[N],inv[N];
    int n;
    Combination(int n = 0) {
        this->n = n;
        init(n);
    }

    void init(int n) {
        inv[0] = fac[0] = fac[1] = 1;
        for(int i = 2;i <= n;i ++) {
            fac[i] = fac[i - 1] * i % P;
        }
        inv[n] = ksm(fac[n],P - 2);
        for(int i = n - 1;i >= 1;i --) {
            inv[i] = inv[i + 1] * (i + 1) % P;
        }
    }

    ll C(ll n,ll m) {
        if(n < 0 || m < 0) return 0;
        return fac[n] * inv[m] % P * inv[n - m] % P;
    }

    ll A(ll n,ll m) {
        assert(n >= m);
        return fac[n] * inv[n - m] % P;
    }

    ll rev(ll x) {
        return ksm(x,P - 2);
    }

    ll vfac(int n) {
        return inv[n];
    }

    ll mfac(int n) {
        return fac[n];
    }
}comb(2010);
int Vnorm(int x) {
    if (x < 0) {
        x += P;
    }
    if (x >= P) {
        x -= P;
    }
    return x;
}
template<class T>
T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}
struct Mint {
    int x;
    Mint(int x = 0) : x(Vnorm(x)) {}
    Mint(i64 x) : x(Vnorm(x % P)) {}
    int val() const {
        return x;
    }
    Mint operator-() const {
        return Mint(Vnorm(P - x));
    }
    Mint inv() const {
        assert(x != 0);
        return power(*this, P - 2);
    }
    Mint &operator*=(const Mint &rhs) {
        x = i64(x) * rhs.x % P;
        return *this;
    }
    Mint &operator+=(const Mint &rhs) {
        x = Vnorm(x + rhs.x);
        return *this;
    }
    Mint &operator-=(const Mint &rhs) {
        x = Vnorm(x - rhs.x);
        return *this;
    }
    Mint &operator/=(const Mint &rhs) {
        return *this *= rhs.inv();
    }
    friend Mint operator*(const Mint &lhs, const Mint &rhs) {
        Mint res = lhs;
        res *= rhs;
        return res;
    }
    friend Mint operator+(const Mint &lhs, const Mint &rhs) {
        Mint res = lhs;
        res += rhs;
        return res;
    }
    friend Mint operator-(const Mint &lhs, const Mint &rhs) {
        Mint res = lhs;
        res -= rhs;
        return res;
    }
    friend Mint operator/(const Mint &lhs, const Mint &rhs) {
        Mint res = lhs;
        res /= rhs;
        return res;
    }
    friend std::istream &operator>>(std::istream &is, Mint &a) {
        i64 v;
        is >> v;
        a = Mint(v);
        return is;
    }
    friend std::ostream &operator<<(std::ostream &os, const Mint &a) {
        return os << a.val();
    }
};
int a[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int n,m,k;
    cin >> n >> m >> k;
    Mint ans;
    for(int i = 1;i <= n;i ++) cin >> a[i];
    for(int i = 1;i <= m;i ++) {
        int zer = 0,rem = n - k + 1;
        for(int j = 1;j <= n;j ++) {
            if(a[j] >= i) rem --;
            if(a[j] == 0) zer  ++;
        } 
        if(rem < 0 || rem > zer) {
            ans = ans + (rem < 0 ? 1 : 0);
            continue;
        }
        Mint p = (m - i + 1) * ksm(m,P - 2);
        vector <Mint> dp1(zer + 1,1),dp2(zer + 1,1);
        for(int j = 0;j < zer;j ++) {
            dp1[j + 1] = dp1[j] * p;
            dp2[j + 1] = dp2[j] * (1 - p);
        }   
        for(int j = rem;j <= zer;j ++) ans = ans + comb.C(zer,j) * dp1[j] * dp2[zer - j];
    }
    cout << ans << endl;
    return 0;
}

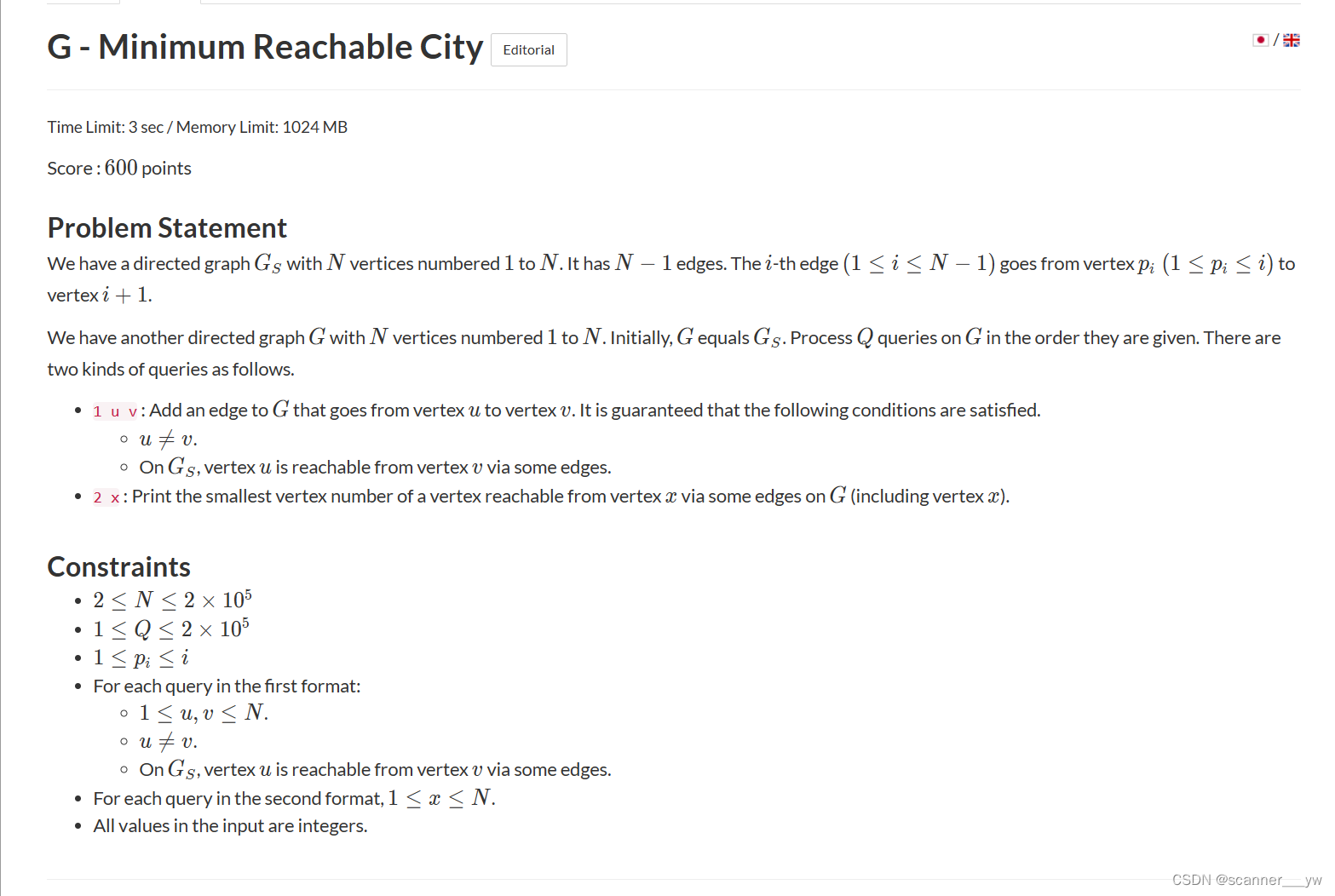
G - Minimum Reachable City (atcoder.jp)

（1）题目大意

给你N个顶点，N-1条有向边，有Q个询问，第一种类型的询问u-->v连接一条有向边，第二种类型的询问是查询x这个节点能到的最小节点的编号是多少？

（2）解题思路

考虑并查集，第一个询问若x，y不在同一个集合，则查询x的根节点，并把当前根节点和该根节点的父亲并起来即可，第二个询问直接输出x的根节点即可。

（3）代码实现

#include <iostream>
#include <map>
#include <set>
#include <vector>
#include <cstring>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <cmath>
#include <unordered_map>
#include <deque>
#include <bitset>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 3e5 + 10;
int p[N],f[N];
int find(int x)
{
    if(x == f[x]) return x;
    return f[x] = find(f[x]);
}
bool same(int x,int y)
{
    return find(x) == find(y);
}
void merge(int x,int y)
{
    x = find(x);
    y = find(y);
    f[x] = y;
}
void solve()
{
    int n,x;
    cin >> n;
    rep(i,2,n) cin >> p[i];
    rep(i,1,n) f[i] = i;
    int Q;
    cin >> Q;
    while(Q --) {
        int op,x,y;
        cin >> op;
        if(op == 1) {
            cin >> x >> y;
            while(!same(x,y)) {
                x = find(x);
                merge(x,p[x]);
            }
        }
        else {
            cin >> x;
            cout << find(x) << endl;
        }
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int T = 1;
    // cin >> T;
    while(T --) solve();
    return 0;
}