Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
Follow up:
Can you solve it without using extra space?
Analysis
First, think strightforward, use Linked List Cycle I method, to see if there is cycle. if does, scan from start node for each node to check whether it is in a cycle, this is O(n^2). But think deeply, this is mathmatical question.
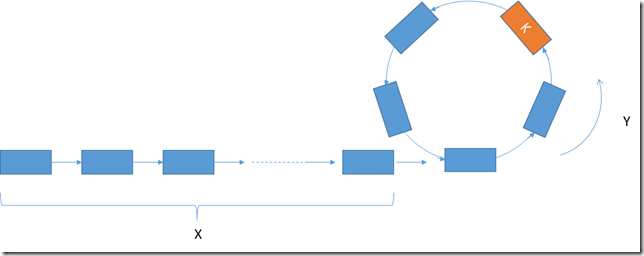
Like the picture shows below: assume linked list has cycle,the length of cycle is Y,the length outside cycle is X.
two pointers, one goes one step per time, another goes two steps per time. If they went t times and meet at the K node
for pointer 1: t = X+nY+K
for pointer 2: 2t = X+mY+K (m,n is unknown)
From above equation, we could get:
2X + 2nY + 2K = X + mY + K
=> X+K = (m-2n)Y
It is clear that the relationship between X and K is complementary based on Y. Which is to say, if pointer 1 goes X steps from start node and pointer 2 goes
X steps form K node. They will meet at the start place of cycle. Complexity is O(n)
Java
public ListNode detectCycle(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while(fast != null && fast.next != null){
slow = slow.next;
fast = fast.next.next;
if(slow == fast)
break;
}
if(fast == null || fast.next == null)
return null;
slow = head;
while(slow != fast){
slow = slow.next;
fast = fast.next;
}
return fast;
}c++
ListNode *detectCycle(ListNode *head) {
ListNode *slow = head;
ListNode *fast = head;
while(fast != NULL && fast->next != NULL){
slow = slow->next;
fast = fast->next->next;
if(slow == fast)
break;
}
if(fast == NULL || fast->next == NULL)
return NULL;
slow = head;
while(slow != fast){
slow = slow->next;
fast = fast->next;
}
return fast;
}







 本文介绍了一种高效的方法来确定链表中循环的起始节点,通过使用快慢指针并结合数学分析,避免了额外空间的使用,实现了O(n)的时间复杂度。
本文介绍了一种高效的方法来确定链表中循环的起始节点,通过使用快慢指针并结合数学分析,避免了额外空间的使用,实现了O(n)的时间复杂度。
















 788
788

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








