二叉树

树的几个概念：父节点、子节点、兄弟节点、根节点、叶子节点（叶节点）、高度、深度、层。
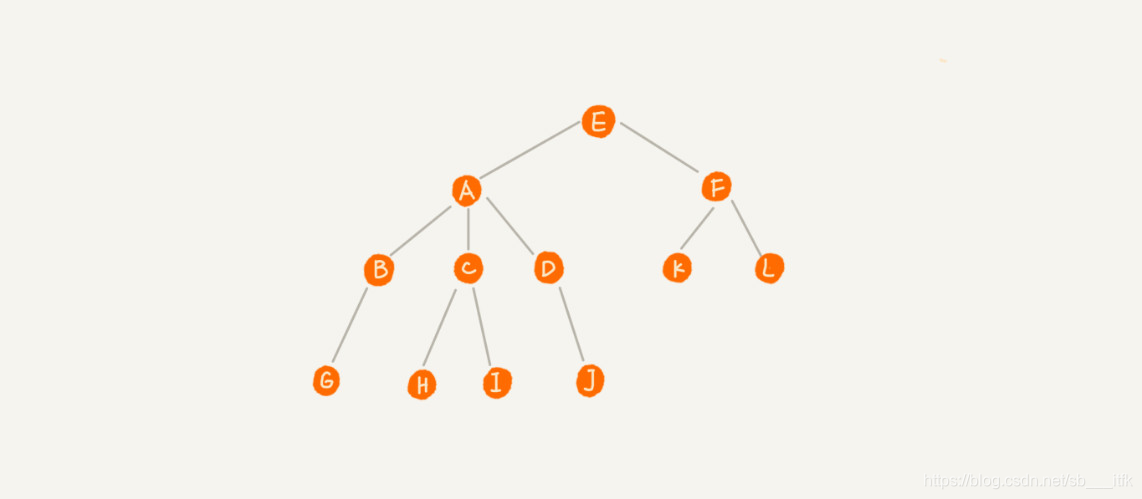A 节点就是 B 节点的父节点，B 节点是 A 节点的子节点。B、C、D 这三个节点的父节点是同一个节点，所以它们之间互称为兄弟节点。我们把没有父节点的节点叫作根节点，也就是图中的节点 E。我们把没有子节点的节点叫作叶子节点或者叶节点，比如图中的 G、H、I、J、K、L 都是叶子节点。
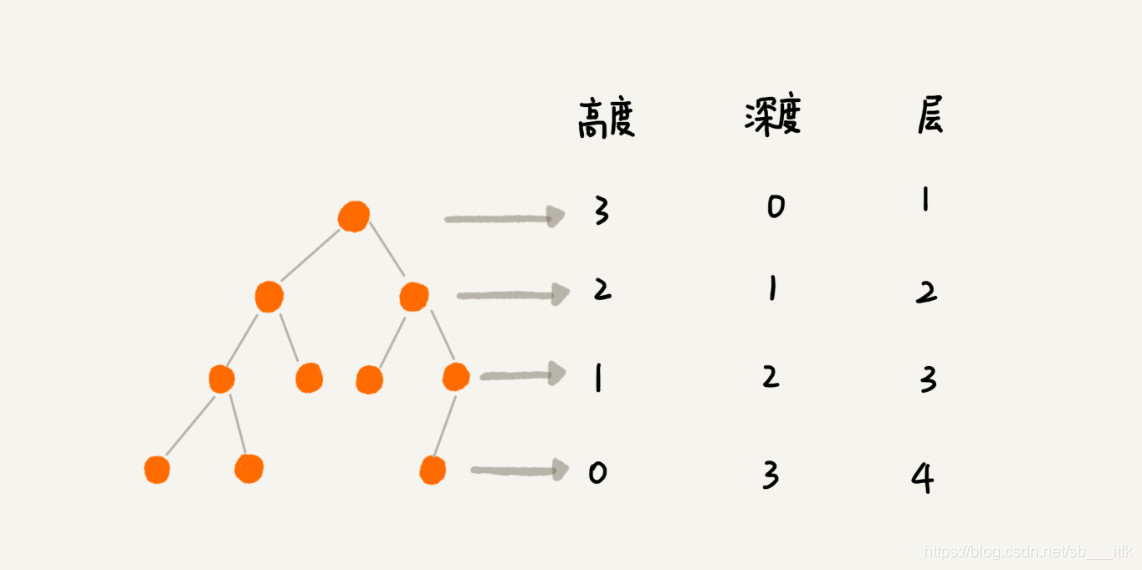二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子节点和右子节点。
除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫作满二叉树。
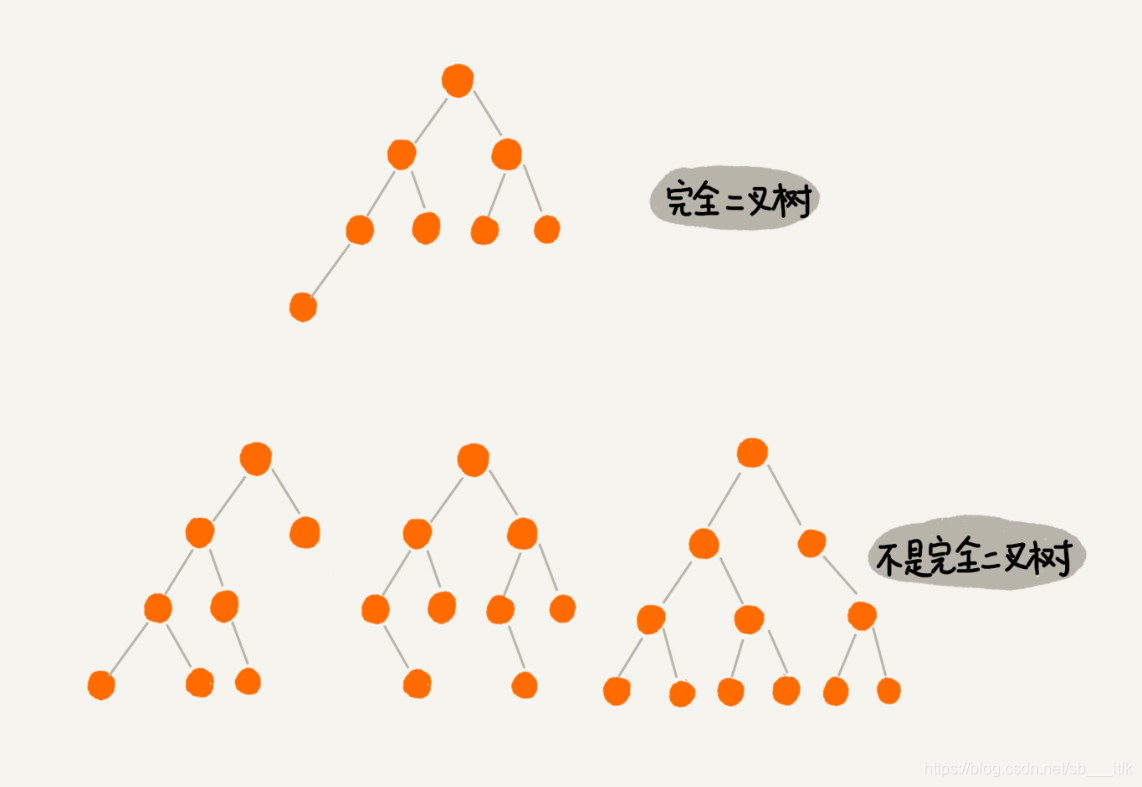
叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫作完全二叉树。满二叉树又是完全二叉树的一种特殊情况。
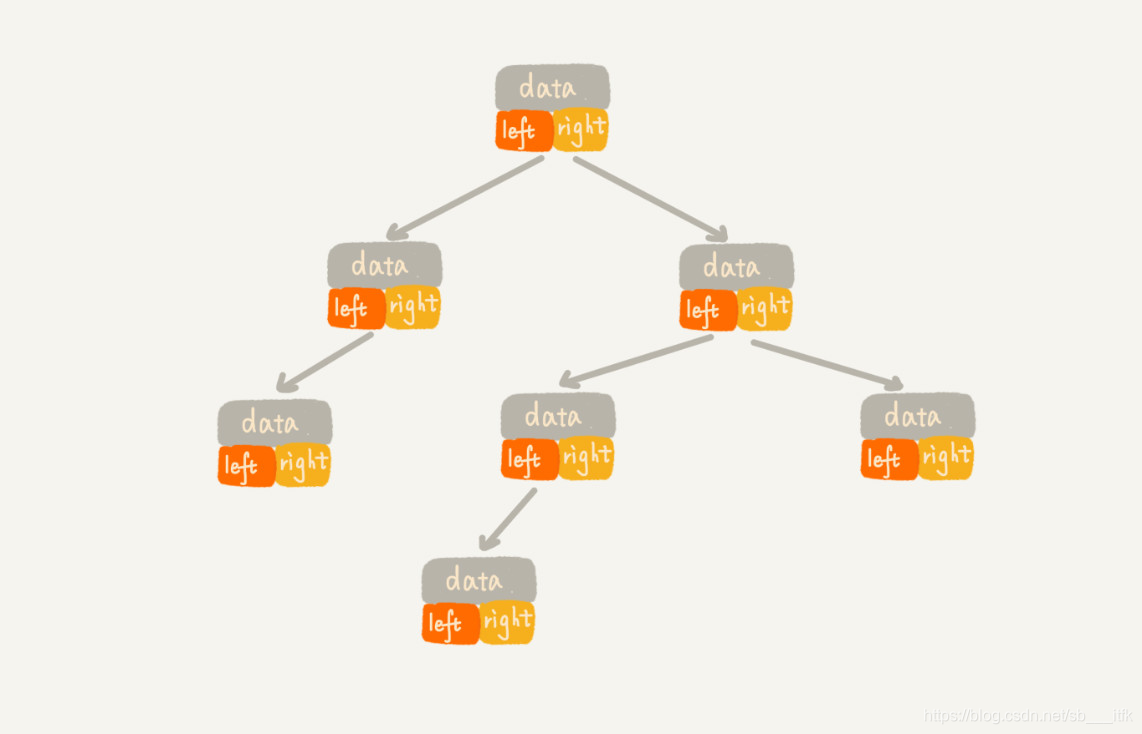
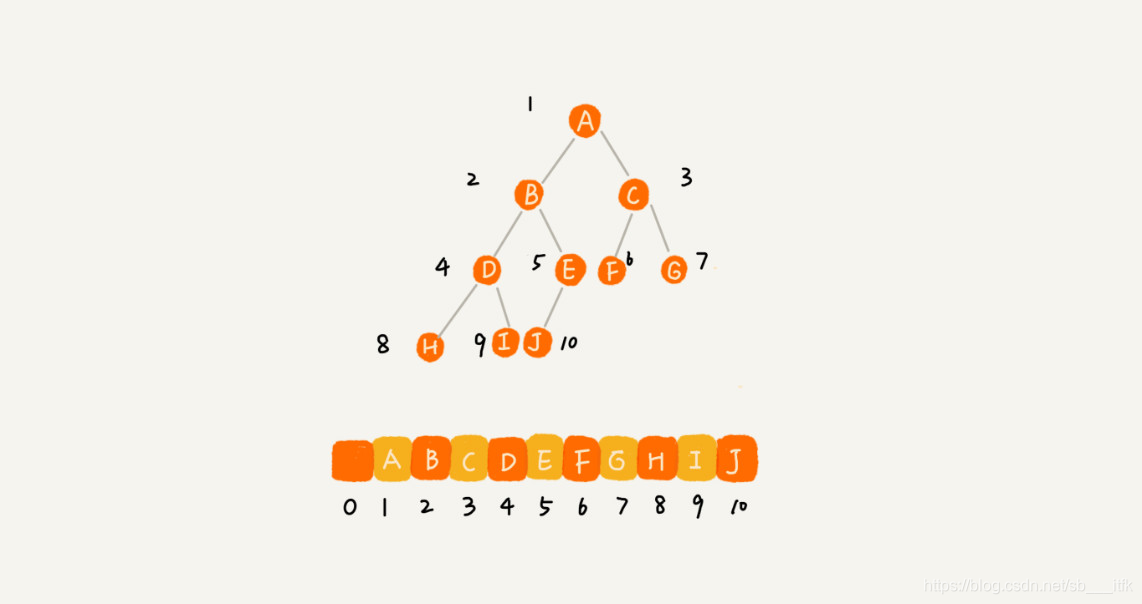
存储一棵二叉树两种方法，一种是基于指针或者引用的二叉链式存储法，一种是基于数组的顺序存储法。
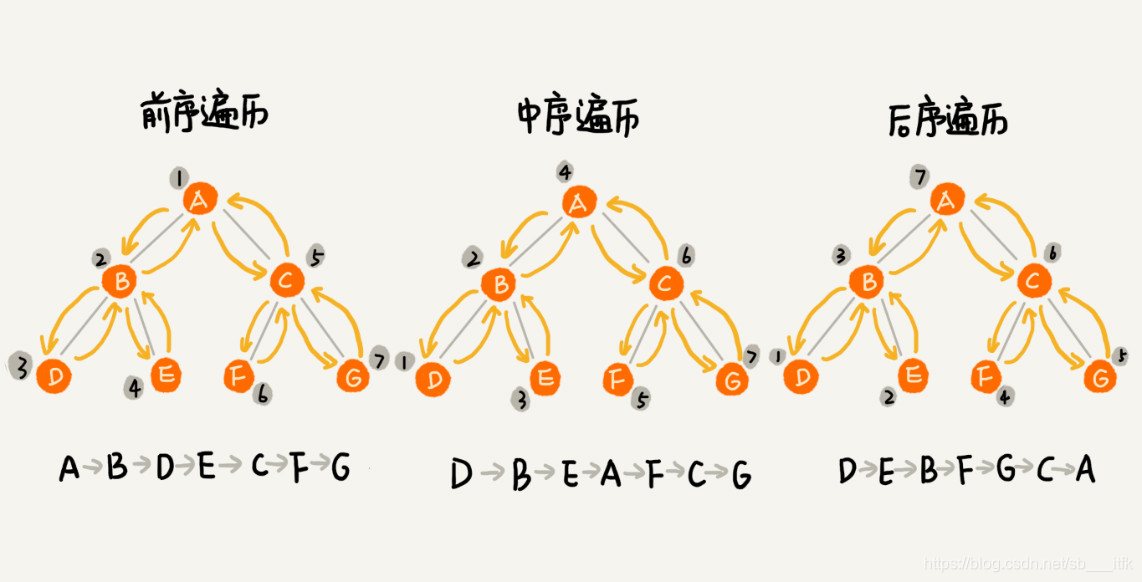
二叉树的遍历，前序遍历、中序遍历和后序遍历。
前序遍历是指，对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。
中序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。
后序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。
二叉树遍历的时间复杂度是 O(n)。

package binarytree

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func preOrderTraversal(root *TreeNode) []int {
	if root == nil {
		return nil
	}
	if root.Left == nil && root.Right == nil {
		return []int{root.Val}
	}
	var stack []*TreeNode
	var res []int
	stack = append(stack, root)
	for len(stack) != 0 {
		e := stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		res = append(res, e.Val)
		if e.Right != nil {
			stack = append(stack, e.Right)
		}
		if e.Left != nil {
			stack = append(stack, e.Left)
		}
	}
	return res
}

func inOrderTraversal(root *TreeNode) []int {
	if root == nil {
		return nil
	}
	if root.Left == nil && root.Right == nil {
		return []int{root.Val}
	}
	res := inOrderTraversal(root.Left)
	res = append(res, root.Val)
	res = append(res, inOrderTraversal(root.Right)...)

	return res
}

func postOrderTraversal(root *TreeNode) []int {
	if root == nil {
		return nil
	}
	var res []int
	if root.Left != nil {
		lres := postOrderTraversal(root.Left)
		if len(lres) > 0 {
			res = append(res, lres...)
		}
	}
	if root.Right != nil {
		rres := postOrderTraversal(root.Right)
		if len(rres) > 0 {
			res = append(res, rres...)
		}
	}
	res = append(res, root.Val)
	return res
}

以上内容摘自《数据结构与算法之美》课程，来学习更多精彩内容吧。