Octave Convolution 八度卷积

最新推荐文章于 2023-10-30 17:12:56 发布
原创 最新推荐文章于 2023-10-30 17:12:56 发布 · 2.5k 阅读 · 15 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文介绍了Facebook提出的Octave Convolution（八度卷积），一种旨在减少计算量和显存占用的卷积方法。通过将特征图分为高频和低频部分，八度卷积在低频部分降低维度，同时保持高频信息。实验表明，这种方法在ResNet/ResNeXt系列网络中提高了性能，降低了计算复杂度，并且适用于不同类型的卷积操作。

Facebook在2019年时推出了一种新的卷积方法，叫做Octave Convolution，中文名是八度卷积。这个名字借鉴了音乐中高音低音的命名方法，来表示图像中高低频的数据。

图像和特征图的高低频表示

对于一张图片来说，低频的数据是比较平滑的部分，也就是图像的整体结构，高频的数据是那些细节的纹理，也就是边缘像素变化比较大的部分。如图1(a)所示。

图1. 图像和特征图的高低频表示
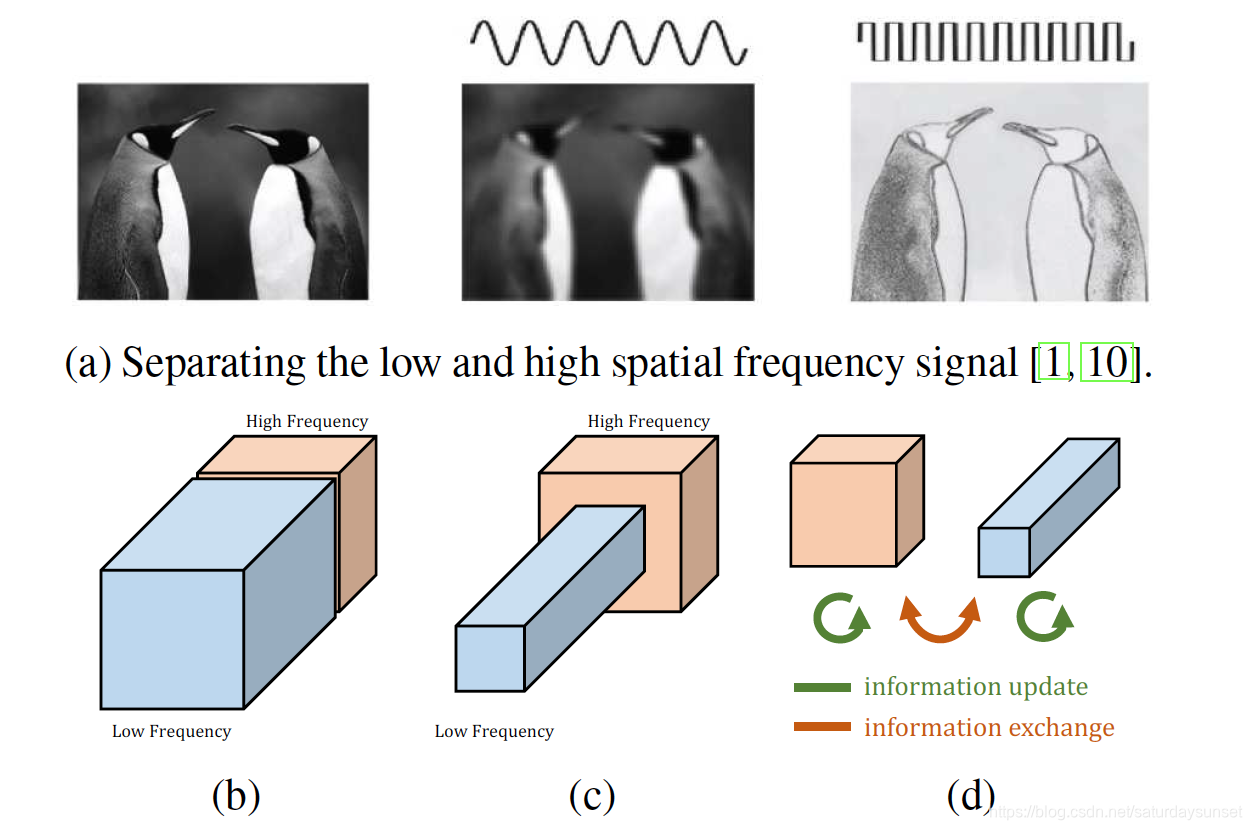
在这里插入图片描述

图1(a)中左图是一张企鹅的原始图片，中间是图片分离出来的低频的部分，也就是整体轮廓图，右图是图像的高频部分，也就是图片的边缘图（有点像素描）。

图1(b)是普通卷积特征图，通常情况下可以分成高频和低频两个部分。由于低频部分的特征基本上比较平滑，所以在特征图上其实不需要和高频一样的维度去表达图像的信息，如图1（c）所示，论文在低频的特征图上将宽高维度降了一半。

图1(d)表示高低频的特征信息的更新和交换，高低频的特征既有各自频率内的卷积操作，也有低频向高频和高频向低频的特征交换和融合，具体怎么操作下面会介绍。

八度卷积的操作

图2. 八度卷积的操作方式
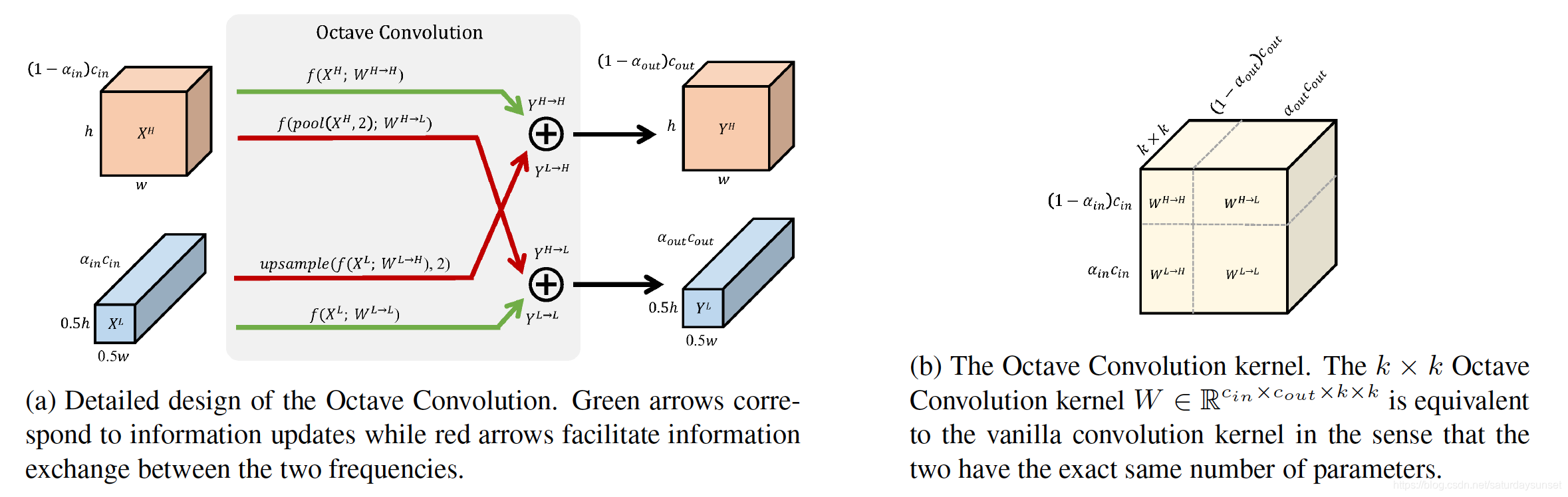
在这里插入图片描述

八度卷积的具体操作方式如图2(a)所示。其中αin\alpha_{in}αin​和αout\alpha_{out}αout​是输入和输出特征图的低频维度在总维度中的占比，在论文中一般假设αin=αout\alpha_{in}=\alpha_{out}αin​=αout​。图2(b)中间绿色的线表示高低频在各自频域内的卷积，卷积核分别是WH→HW^{H\rightarrow H}WH→H和WL→LW^{L\rightarrow L}W

最低0.47元/天 解锁文章
神经网络学习之OctConv：八度卷积
qq_41726230的博客
11-13 6197
八度卷积的学习。特征图可以根据频率大小分为高频和低频，其中低频特征图又因为存在大量冗余信息，需要降低其分辨率。不同频率的特征图对应不同大小的卷积核，八度卷积核由四部分组成。八度卷积时，不仅有同一频率内的更新还有不同频率之间的交流。
Octave Convolution卷积
吴建明wujianming_110117
03-15 594
Octave Convolution卷积 MXNet implementation 实现for: Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution ImageNet Ablation • Loss: Softmax • Learning rate: Cosine (warm-up: 5 epochs, lr: 0.4) • MXNet API: Symbol
Octave卷积学习笔记
月见樽
05-05 2365
本文首发于个人博客 Octave卷积 Octave卷积的主题思想来自于图片的分频思想，首先认为图像可进行分频： 低频部分：图像低频部分保存图像的大体信息，信息数据量较少 高频部分：图像高频部分保留图像的细节信息，信息数据量较大 由此，认为卷积神经网络中的feature map也可以进行分频，可按channel分为高频部分和低频部分，如图所示： 对于一个feature map，将其按通道分...
Octave Convolution-八度卷积
qq_40723205的博客
12-06 581
来源：ICCV 2019 论文题目：Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution OctConv（Octave Convolution）是一个即插即用的结构在提高精度的同时，节约计算资源的消耗。 (a)自然图像可以分解为低空间频率和高空间频率两部分。 (b)卷积层的输出图也可以根据其空间频率分解和分组。 因此文章使用一个系数将特征图显示因式分解为
『深度概念』一文读懂Octave Convolution（OctConv）八度卷积
简明AI工作室
08-15 9736
RyanXing Multimedia Processing & Computer Vision. Paper | Octave Convolution（OctConv） 论文：Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution 1....
学习记录——Octave Convolution、LSK
Chaoy6565的博客
07-31 485
自然世界中的图像存在高低频，卷积层的输出特征图以及输入通道，也都存在高、低频分量。低频分量支撑的是整体轮廓，高频分量则关注细节，显然，低频分量是存在冗余的，在编码过程中可以节省。下图直观地展示了八度卷积的卷积核，可以看出四个部分共同组成了大小为 k*k 的卷积核。其中，in和out分别表示输入和输出特征图的相关属性，在这篇文章中，输入的低频占比、通道数量都和输出的一致。八度卷积的思想是为处理输入数据提供两个单独的路径：一个用于高频（细粒度）信息，另一个用于低频（粗粒度）信息。
精选资源
OctaveConv-Pytorch:拖放八度的PyTorch实现
03-16
OctaveConv-Pytorch 程的PyTorch实现 （培训进行中） 用法 from resnet import octResnet50 ... model = octResnet50 () 从
八度卷积代码实现
shananshuibei的博客
04-25 780
忘记从哪个大佬那摘下来了
Octave Convolution
10-24 269
Paper：Octave Convolution Github：Offical 和 UnOffical Octave是指八音阶，在音乐中降低八音阶代表频率减半。 Abstract 自然图像中的信息可以被分解为低频信息和高频信息，低频信息通常是全局结构而高频信息通常是细节信息。类似，卷积的输出特征图也可看作是低频信息和高频信息的混合。 Ocave Convolution将特征图进行分解，...
Octave Convolution学习笔记 （附代码）
PLANTTHESON的博客
10-30 852
Octave Convolution学习笔记 （附代码）
【轻量级网络】Octave Convolution
筱
05-13 1160
Paper：OctConv Github：Offical 和 UnOffical
【Paper & Code】（CVPR2019）Octave Convolution
穆友航的博客
05-19 530
亮点 分离图像数据中的高频和低频信息，降低低频信息的分辨率，保持高频信息的分辨率，减少了整体运算量。 论文介绍 代码 MXNet Symbol接口下的实现：OctConv ...
八分音符(频率)卷积算子 Octave Convolution
zhy_Learn的博客
08-14 147
为什么读此系列文章？ 优化数学和计算理论帮助机器学习完成问题分类： 1)按照领域划分，比如计算机视觉，自然语言处理，统计分析预测形； 2)按照算法复杂划分，比如是否是NP-Hard问题，是否需要精确解； 3)按照方法分类，监督性学习问题，非监督性学习问题，半监督性学习模型，和有先验信息的交互学习模型...
OctConv：八度卷积复现
华为云官方博客
04-12 1940
不同于传统的卷积，八度卷积主要针对图像的高频信号与低频信号。
基于深度学习的铁路异物侵限检测算法研究_整体认知感觉欠点意思，但是有一个新的变形卷积-Octave 卷积
白水空空
08-19 2179
相似的，对于卷积层输出的特征图也能够看成是不同频率分量的组合，对于输出特征图的低频部分，每一个位置都独立的储存着自己的特征描述子，而忽略了那些可以共同储存和处理的相邻区域的特征描述子，这就造成了在进行卷积运算时不必要的计算量的产生，因此可以将经过卷积层处理后的特征图分解成不同频率的两个部分，在卷积神经网络中，传统的卷积方式是使用一定大小的卷积核上的每一个元素乘以原图片或特征图上相应位置的特征值，最后相加，将得到的数值作为经过卷积操作的到的特征图上对应位置的特征值，具体计算公式如式。
Octave Convolution[论文详解]
热门推荐
gdtop的个人笔记
04-16 2万+
Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution[github] 传统的卷积运算，要成为过去时了。Facebook和新加坡国立大学联手提出了新一代替代品：OctConv（OctaveConvolution），效果惊艳，用起来还非常方便。Oct...
模型压缩与加速:Octave Convolution
撸猫写博客
04-28 863
  自AlexNet刷新了ImageNet比赛的最佳记录以来,神经网络的又一次高潮猛烈的到来了.一些列各种各样的网络层出不穷,图像/音频/文本等各种任务下都开始了神经网络一统天下的声音.然而神经网络虽然很火,近些年在落地端却鲜有比较成功的案例,其中一个很重要的原因是这些网络需要很强的计算资源,基本都要跑在PC或者服务器上.因此个人认为深度学习如果想在工业上获得比较大的推广和应用,解决模型大小与推理...
实验笔记之——基于RRDBNet的Octave Convolution实验记录
gwpscut的博客
05-09 6916
本博文对RRDBNET进行改进，将里面的conv层改为octave conv层。 关于ESRGAN可以参考本文之前的博客《基于pytorch的ESRGAN（论文阅读笔记+复现）》 先复现RRDBNET ​ ​ 网络结构 #############################################################################...
实验笔记之——基于SRResNet的Octave Convolution实验记录
gwpscut的博客
04-30 3815
先给出论文的链接（https://arxiv.org/pdf/1904.05049.pdf） github连接（https://github.com/terrychenism/OctaveConv/） 本博文为文章《Drop an Octave Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Co...
八度卷积
最新发布
04-02
### 八度卷积概述 八度卷积（Octave Convolution, OctConv）是一种旨在降低计算成本并提高模型效率的卷积方法。它通过将特征图分为高分辨率和低分辨率两部分来减少冗余计算，从而优化资源利用[^4]。 具体来说，在传统的卷积神经网络中，每一层都会对整个输入图像进行密集的操作，这可能导致大量的重复计算以及不必要的内存消耗。而八度卷积则引入了一种分层次的方法：一部分数据保持较高的分辨率用于捕捉细节信息；另一部分被下采样到较低分辨率以提取更广泛的上下文信息。这种方法不仅能够有效减少运算次数，还能够在一定程度上维持甚至提升最终性能表现[^5]。 以下是关于八度卷积的具体概念及其算法实现： --- ### 八度卷积的核心原理 八度卷积的主要思想在于将输入张量拆分成高低频两个分支，并分别应用不同尺度上的卷积核对其进行处理后再重新组合起来形成输出结果。这样做的好处是可以让高频部分专注于局部区域内的精细结构变化检测，同时允许低频路径负责更大范围的空间模式识别任务，进而达到节省算力的目的[^6]。 #### 数学表达形式 假设 \( X_h \) 和 \( X_l \) 分别代表原始输入中的高频率子集与低频率子集，则经过一次标准八度变换后的对应输出可以表示如下： \[ Y_h = W_{hh} * D(X_h) + U(W_{lh} * A(X_l)) \] \[ Y_l = V(W_{hl} * P(X_h)) + W_{ll} * D(X_l) \] 其中， - \( W_{ij}, i,j\in{h,l}\): 表示连接各维度间关系权重矩阵； - \( D(\cdot)\),\(P(\cdot)\): 下/上取样的操作符； - \(U,V:\) 调整大小适配器函数。 上述公式清晰展示了如何通过跨级别交互完成端到端训练流程的同时保留足够的灵活性去适应多种应用场景需求[^7]。 --- ### Python 实现代码片段 下面提供了一个基于 PyTorch 的简单版本八度卷积层定义方式作为参考实例: ```python import torch.nn as nn from functools import partial class OctConv(nn.Module): def __init__(self, in_channels, out_channels, kernel_size=3, alpha_in=0.5, alpha_out=0.5, stride=1, padding=1): super(OctConv, self).__init__() self.alpha_in = alpha_in self.alpha_out = alpha_out hi_in_ch = int((1-alpha_in)*in_channels) lo_in_ch = in_channels - hi_in_ch hi_out_ch = int((1-alpha_out)*out_channels) lo_out_ch = out_channels - hi_out_ch self.h2h = None if hi_in_ch==0 or hi_out_ch==0 else \ nn.Conv2d(hi_in_ch, hi_out_ch, kernel_size, stride=stride, padding=padding) self.l2l = None if lo_in_ch==0 or lo_out_ch==0 else \ nn.Conv2d(lo_in_ch, lo_out_ch, kernel_size, stride=stride, padding=padding) self.h2l = None if hi_in_ch==0 or lo_out_ch==0 else \ nn.Sequential( nn.AvgPool2d(kernel_size=(2, 2), stride=2), nn.Conv2d(hi_in_ch, lo_out_ch, kernel_size, stride=stride, padding=padding)) self.l2h = None if lo_in_ch==0 or hi_out_ch==0 else \ nn.Sequential( nn.Upsample(scale_factor=2, mode='nearest'), nn.Conv2d(lo_in_ch, hi_out_ch, kernel_size, stride=stride, padding=padding)) def forward(self,x): x_h, x_l = x if isinstance(x,tuple) else (x,None) h2h = self.h2h(x_h) if self.h2h is not None and x_h is not None else None l2l = self.l2l(x_l) if self.l2l is not None and x_l is not None else None h2l = self.h2l(x_h) if self.h2l is not None and x_h is not None else None l2h = self.l2h(x_l) if self.l2h is not None and x_l is not None else None y_h = h2h.clone() if h2h is not None else 0. y_l = l2l.clone() if l2l is not None else 0. if l2h is not None: y_h += l2h if h2l is not None: y_l += h2l return ((y_h,y_l),(y_h,) )[self.alpha_out<1e-8 ] ``` 此段程序实现了基本功能框架下的前向传播逻辑描述[^8]。 --- ### 深度学习中的实际应用案例分析 在现代计算机视觉领域内，诸如目标检测、语义分割等复杂任务均可以从采用八度卷积技术获得显著收益。例如 MobileNetV3 中便融入了此类机制使得整体架构更加紧凑高效而不失精度优势[^9]。 此外，在视频理解方向也有不少研究探索将其应用于动作分类或者异常事件监测等方面取得不错效果。由于其天然具备多尺度特性因此非常适合用来建模长时间序列依赖关系等问题情境之中[^10]。 ---
评论 6
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值