逻辑回归python实现

对线性函数进行逻辑回归用python实现

前面主要是用octave实现了逻辑回归的算法，但是觉得在实际开发过程中用到octave的并不多，因此还是需要学习python，希望能通过这两天的学习把算法流程搞清楚，需要做什么事情。也使用了sklearn这个库，可以直接调用方法实现，因此缺点是不能看到一些算法的实现过程。

先介绍一下使用python的基本包的作用：

matplotlib帮助画图，numpy处理数值型的数组，pandas处理很多类型的数据。

matplotlib能够将数据可视化，使数据更加客观，更具有说服力，他是用python实现，是最流行的python底层绘图库，主要做数据可视化图表。

plt.xticks()函数设置x轴的刻度

numpy帮助我们处理数值型数据，用于大型、多维数组上执行数值运算

下面这个是进行逻辑回归使用的数据集的展示：

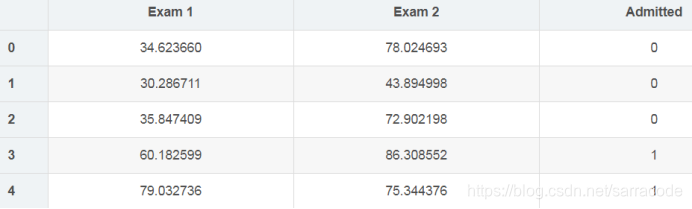
代码如下：

import matplotlib.pyplot as plt
import numpy as np
import scipy.optimize as opt
from sklearn.metrics import classification_report
import pandas as pd


def raw_data(path):
    """
       从文件中读取数据，并把每一列存储到一个列表中，那么存储完之后就如上图所示    
    """

    data=pd.read_csv(path,names=['exam1','exam2','admit'])
    return data


def draw_data(data):
    """
       我的理解是把admit那一列中值为1的那一行数据存储到列表accept中，同理refuse，其中1代表样本是正的（被接纳），0代表样本是负的（未被接纳），并把这两种数据点在图中标注出来，被接纳的用绿色表示，不被接纳的用红色表示
    """

    accept=data[data['admit'].isin([1])]
    refuse=data[data['admit'].isin([0])]
     plt.scatter(accept['exam1'],accept['exam2'],c='g',label='admit')
    plt.scatter(refuse['exam1'],refuse['exam2'],c='r',label='not admit')
    plt.title('admission')
    plt.xlabel('score1')
    plt.ylabel('score2')
    return plt

def sigmoid(z):
    """
       根据公式定义sigmoid函数    
    """
    return 1/(1+np.exp(-z))

def cost_function(theta,x,y):
    """
        百度查了查，发现shape[0]就是读取矩阵第一维度的长度，在这里m就是样本的数量   
a.dot(b) 与 np.dot(a,b)效果相同，都是计算两个矩阵相乘
但需注意，矩阵积计算不遵循交换律,np.dot(a,b) 和 np.dot(b,a) 得到的结果是不一样的

    """
    m=x.shape[0]
    j=(y.dot(np.log(sigmoid(x.dot(theta))))+(1-y).dot(np.log(1-sigmoid(x.dot(theta)))))/(-m)
    return j



def gradient_descent(theta,x,y):
    """
       计算偏导数也就是梯度下降法求最优值 
    """

    return ((sigmoid(x.dot(theta))-y).T).dot(x)

def predict(theta,x):
    """
       这个是根据sigmoid函数的图像得出的结论 
    """
    h=sigmoid(x.dot(theta))
    return [1 if x>=0.5 else 0 for x in h]

def boundary(theta,data):
    """
       绘制出边界曲线
    """
    x1=data['exam1']
    x2=(theta[0]+theta[1]*x1)/-theta[2]
    plt=draw_data(data)
    plt.title('boundary')
    plt.plot(x1,x2)
    plt.show()


def main():
    data=raw_data('venv/lib/dataset/ex2data1.txt')
    x1=data['exam1']
    x2=data['exam2']

    """
       np.c_中的c是column（列）的缩写，是按列叠加两个矩阵的意思，
       也可以说是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等
    
    """
    x=np.c_[np.ones(x1.shape[0]),x1,x2]
    y=data['admit']
    theta=np.zeros(x.shape[1])
      theta=opt.minimize(fun=cost_function,x0=theta,args=(x,y),method='tnc',jac=gradient_descent)
    theta=theta.x
    print(classification_report(predict(theta,x),y))
    boundary(theta,data)

main()

其中有些代码不会查了查，总结如下：

Q（1）x2=(theta[0]+theta[1]*x1)/-theta[2] 什么意思？

A：我把线性回归和逻辑回归给弄混了，线性回归是线性的，只有x0和x1两个特征。其中x0=1。而逻辑回归是分类问题，他需要拟合这两类数据画一条直线，因此其实有x0，x1，x2这三个特征，其中x0=1。那么h(x)=0时，就会变成一个线性函数，x1和x2充当了坐标轴，用来拟合数据，因此正好可以得到上面的式子。

Q（2）我定义了代价函数和梯度下降函数，怎么来最小化目标函数呢？

A：我认为优化的过程是要先求出theta的值，然后把theta带入代价函数中计算，经过很多次的迭代下降，最后使J的值最小。在具体实现时利用了这个函数theta=opt.minimize(fun=cost_function,x0=theta,args=(x,y),method='tnc',jac=gradient_descent)，那么这个函数会返回优化问题的目标数组x，因此再调用theta=theta.x得到优化的对象theta。

代码测试结果如下：

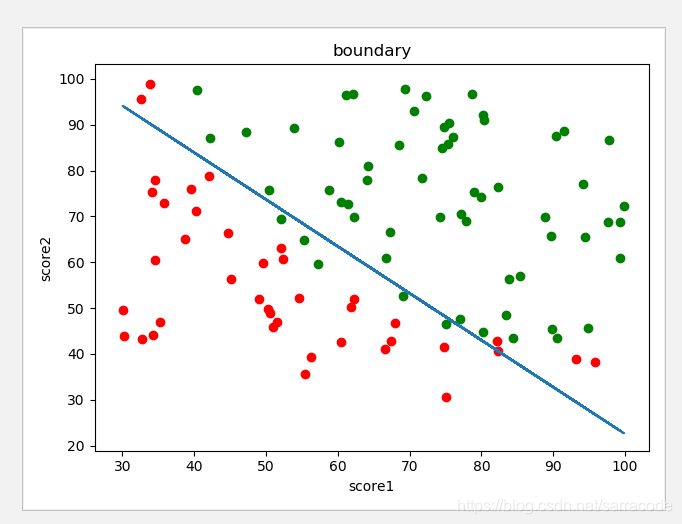
对非线性函数进行逻辑回归用python实现

这个数据集的展示：

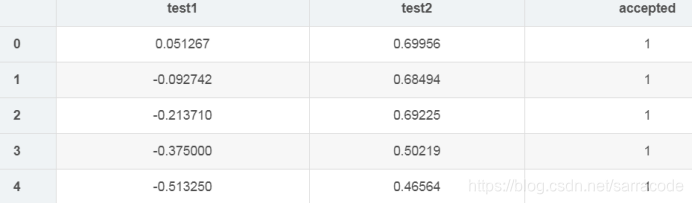
代码如下：

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import linear_model
import scipy.optimize as opt
from sklearn.metrics import classification_report


def raw_data(path):

    """
          调用这个函数读取文件中的数据，然后以上图的格式存储到列表中 
    """

    data=pd.read_csv(path,names=['test1','test2','accept'])
    return data


def draw_data(data):
    accept=data[data['accept'].isin(['1'])]
    reject=data[data['accept'].isin(['0'])]
    plt.scatter(accept['test1'],accept['test2'],c='g')
    plt.scatter(reject['test1'],reject['test2'],c='r')
    plt.title('raw_data')
    plt.xlabel('test1')
    plt.ylabel('test2')
    return plt

def feature_mapping(x1,x2,power):
    """
          这个函数还不太懂 
    """

    datamap={}
    for i in range(power+1):
        for j in range(i+1):
            datamap["f{}{}".format(j,i-j)]=np.power(x1,j)*np.power(x2,i-j)
    return pd.DataFrame(datamap)


def sigmoid(z):
    return 1/(1+np.exp(-z))


def regularized_cost_function(theta,x,y,lam):
    """
          先获取样本的数量m，然后写出吴老师讲的公式
penalty就是偏置项用来正则化
    """

    m=x.shape[0]
    j=((y.dot(np.log(sigmoid(x.dot(theta)))))+((1-y).dot(np.log(1-sigmoid(x.dot(theta))))))/-m
    penalty=lam*(theta.dot(theta))/(2*m)
    return j+penalty


def regularized_gradient_descent(theta,x,y,lam):
    m=x.shape[0]
    partial_j=((sigmoid(x.dot(theta))-y).T).dot(x)/m
    partial_penalty=lam*theta/m
    partial_penalty[0]=0
    return partial_j+partial_penalty


def predict(theta,x):
    h=x.dot(theta)
    return [1 if x>=0.5 else 0 for x in h]


def boundary(theta,data):

    """
          这个函数还不太懂 
    """

    x = np.linspace(-1, 1.5, 200)
    x1, x2 = np.meshgrid(x, x)
    z = feature_mapping(x1.ravel(), x2.ravel(), 6).values
    z = z.dot(theta)
    z = z.reshape(x1.shape)
    plt=draw_data(data)
    plt.contour(x1,x2,z,0)
    plt.title('boundary')
    plt.show()


def main():
    rawdata=raw_data('venv/lib/dataset/ex2data2.txt')
        data=feature_mapping(rawdata['test1'],rawdata['test2'],power=6)
    
    x=data.values
    y=rawdata['accept']
    theta=np.zeros(x.shape[1])
        theta=opt.minimize(fun=regularized_cost_function,x0=theta,args=(x,y,1),method='tnc',jac=regularized_gradient_descent).x
    boundary(theta,rawdata)


main()

Q（1）feature_mapping(x1,x2,power)这个函数的是干嘛的？

A：这个函数是构建多项式特征值，应该是h(x)=1+x1+x2+x^2+x1x2+x^2+...

那么这个是6次的，因此会很长，就是创建这样的假设函数，然后带入代价函数和梯度函数求最小化的目标值theta，最后使用画图把图画出来。

部分参考此篇博客链接https://blog.youkuaiyun.com/zy1337602899/article/details/84777396