排序技术
定义Sort类
class Sort
{
public:
Sort(int r[], int n);//构造函数,生成待排序序列
~Sort();//析构函数
void InsertSort();//直接插入排序
void ShellSort();//希尔排序
void BubbleSort();//气泡排序
void QuickSort(int first, int last);//快速排序
void SelectSort();//简单选择排序
void HeapSort();//堆排序
void MergeSort1(int first, int last);//二路归并递归排序
void MergeSort2();//二路归并非递归排序
void Print();//输出序列
private:
int Partition(int first, int last);//快速排序,一次划分
void Sift(int k, int last);//堆排序,堆调整
void Merge(int first1, int last1, int last2);//归并排序,合并相邻有序序列
void MergePass(int h);//归并排序,一趟归并
int* data;
int length;
};
-
[插入排序图解]( (14条消息) 插入排序(图解)_RainySouL1994的博客-优快云博客 )
-
[希尔排序图解]( (14条消息) 排序算法 —— 希尔排序(图文超详细)_与大师约会的博客-优快云博客 )(希尔排序可以理解成有增量为d的直接插入排序)
-
[气泡排序]( (14条消息) [排序算法]图解冒泡排序(多图+解决两种无效比较问题)_冒泡排序图解_会敲键盘的肘子的博客-优快云博客 )
-
快速排序

-
[简单选择排序图解]( (14条消息) [排序算法]图解简单选择排序(图解堪比Debug显示每次循环结果)_会敲键盘的肘子的博客-优快云博客 )
-
二路归并排序图解
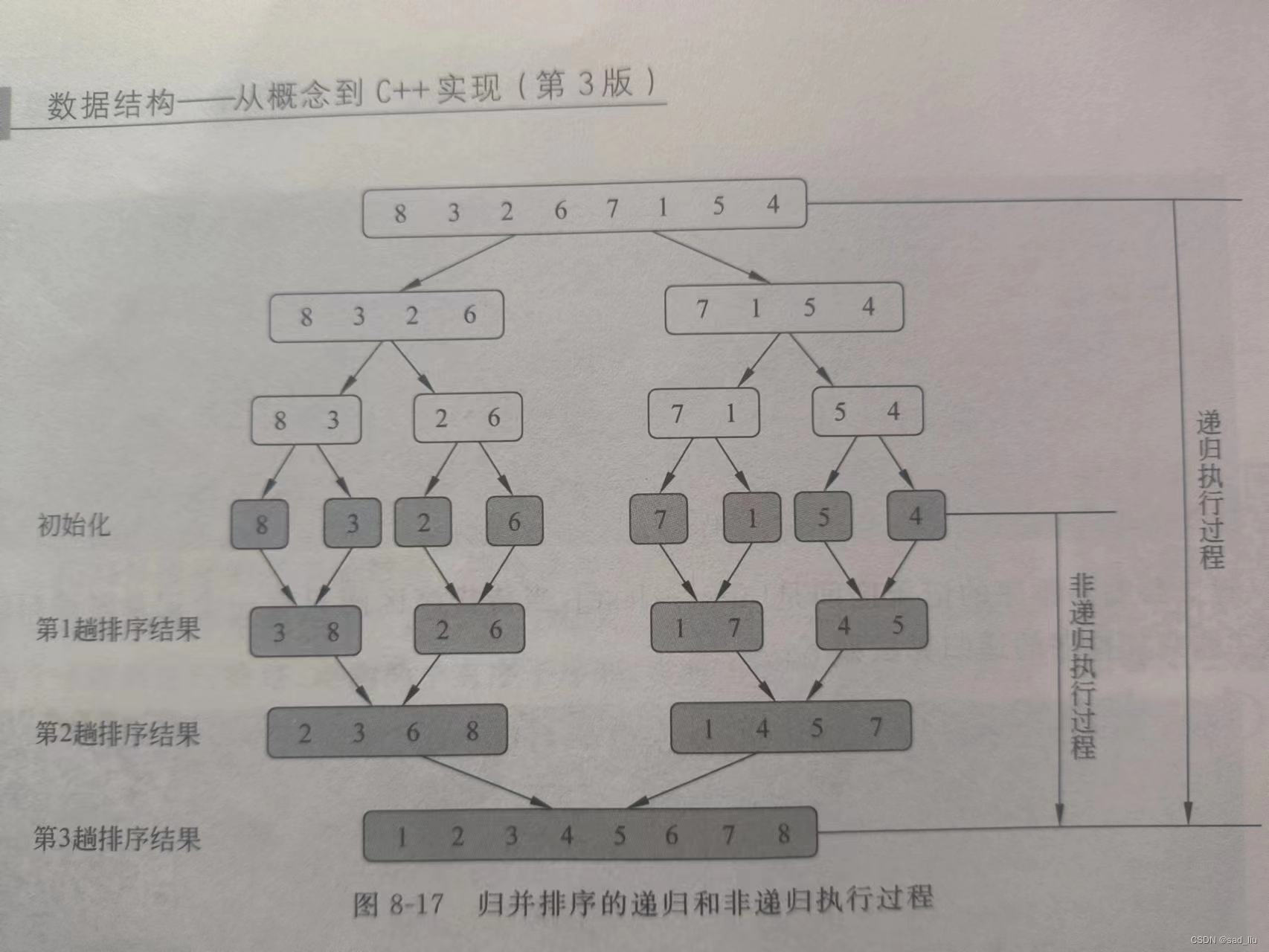
源码展示
Sort.h
#pragma once
#include <iostream>
#include <cmath>
using namespace std;
class Sort
{
public:
Sort(int r[], int n);//构造函数,生成待排序序列
~Sort();//析构函数
void InsertSort();//直接插入排序
void ShellSort();//希尔排序
void BubbleSort();//气泡排序
void QuickSort(int first, int last);//快速排序
void SelectSort();//简单选择排序
void HeapSort();//堆排序
void MergeSort1(int first, int last);//二路归并递归排序
void MergeSort2();//二路归并非递归排序
void Print();//输出序列
private:
int Partition(int first, int last);//快速排序,一次划分
void Sift(int k, int last);//堆排序,堆调整
void Merge(int first1, int last1, int last2);//归并排序,合并相邻有序序列
void MergePass(int h);//归并排序,一趟归并
int* data;
int length;
};
Sort::Sort(int r[], int n)
{
data = new int[n];
for (int i = 0; i < n; i++)
{
data[i] = r[i];
}
length = n;
}
Sort::~Sort()
{
delete[] data;
}
void Sort::Print()
{
for (int i = 0; i < length; i++)
{
cout << data[i] << "\t";
}
cout << endl;
}
void Sort::InsertSort()
{
int i, j, temp;
for (i = 1; i < length; i++)//排序进行length-1躺
{
temp = data[i];//暂存待插记录
for (j = i-1; j >= 0 && temp < data[j]; j--)//寻找插入位置
{
data[j + 1] = data[j];
}
data[j+1] = temp;
}
}
void Sort::ShellSort()
{
int i, j, d, temp;
for (d = length / 2; d >= 1; d = d / 2)//增量为d进行直接插入排序
{
for (i = d; i < length; i++)//进行一趟希尔排序
{
temp = data[i];//暂存待插记录
for (j = i - d; j >= 0 && temp < data[j]; j = j - d)
{
data[j + d] = data[j];//记录后移d个位置
}
data[j + d] = temp;
}
}
}
//冒泡排序优化1
void Sort::BubbleSort()
{
int i, j, temp, flag = 1;
for (i = 1; i < length && flag == 1; i++)
{
flag = 0;
for (j = 0; j < length - i; j++)
{
if (data[j] > data[j + 1])
{
flag = 1;
temp = data[j];
data[j] = data[j + 1];
data[j + 1] = temp;
}
}
}
}
//冒泡排序优化2
//void Sort::BubbleSort()
//{
// int j, exchange, bound, temp;
// exchange = length - 1;
// while (exchange != 0)
// {
// bound = exchange;
// exchange = 0;
// for (j = 0; j < bound; j++)
// {
// if (data[j] > data[j + 1])
// {
// temp = data[j];
// data[j] = data[j + 1];
// data[j + 1] = temp;
// exchange = j;//记载每次交换的位置
// }
// }
// }
//}
int Sort::Partition(int first, int last)
{
int i = first, j = last, temp;//初始化一次划分的区间
while (i < j)
{
while (i < j && data[i] <= data[j])//右侧扫描
{
j--;
}
if (i < j)
{
temp = data[i];
data[i] = data[j];
data[j] = temp;
i++;//不能遗漏
}
while (i < j && data[i] <= data[j])//左侧扫描
{
i++;
}
if (i < j)
{
temp = data[i];
data[i] = data[j];
data[j] = temp;
j--;//不能遗漏
}
}
return i;//i为轴值记录的最终位置 return要写在while外面 看了好久才查出来555...
}
void Sort::QuickSort(int first, int last)
{
if (first >= last)//区间长度为1,递归结束
{
return;
}
else
{
int pivot = Partition(first, last);//一次划分
QuickSort(first, pivot - 1);//对左侧子序列进行快速排序
QuickSort(pivot + 1, last);//对右侧子序列进行快速排序
}
}
void Sort::SelectSort()
{
int i, j, temp, index;
for (i = 0; i < length - 1; i++)
{
index = i;
for (j = i + 1; j < length; j++)
{
if (data[j] < data[index])
{
index = j;
}
}
if (index != i)
{
temp = data[index];
data[index] = data[i];
data[i] = temp;
}
}
}
//大根堆为例
void Sort::Sift(int k, int last)
{
int i, j, temp;
i = k, j = 2 * i + 1;//i是被调整结点,j是i的左孩子
while (j <= last)//还没有进行到叶子节点
{
//确保j是两个孩子中较大的那个
/*
这样做的目的是为了确保在建堆的过程中,选取能够满足堆的性质的节点。通过比较左右孩子节点的值,
选择较大的值作为下一次迭代的节点,以便继续向下调整堆结构,最终使整个数组达到堆的性质。
换句话说,通过这一步的判断,可以保证在每次交换结点后,始终将较大的元素向上移动,从而实现堆的调整和排序。
*/
if (j < last && data[j] <= data[j + 1])//j<last确保j+1不越界
{
j++;
}
if (data[i] > data[j])//已经是堆
{
break;
}
else
{
temp = data[i];
data[i] = data[j];
data[j] = temp;
//被调整结点位于结点j的位置,检索到叶子结点才结束
i = j;
j = 2 * i + 1;
}
}
}
void Sort::HeapSort()
{
int i, temp;
for (i = (length / 2) - 1; i >= 0; i--)//ceil()向上取整函数
{
//从最后一个分支结点至根结点调整
Sift(i, length - 1);
}
for (i = 1; i < length; i++)//length个数据 走length-1趟 下标弄清楚
{
temp = data[0];
data[0] = data[length - i];
data[length - i] = temp;
Sift(0, length - i - 1);//重建堆
}
}
void Sort::Merge(int first1, int last1, int last2)
{
int* temp = new int[length];//数组temp作为合并的辅助空间
memset(temp, 0, length);
int i, j, k;
i = first1, j = last1 + 1, k = first1;
while (i <= last1 && j <= last2)
{
if (data[i] <= data[j])
{
temp[k++] = data[i++];
}
else
{
temp[k++] = data[j++];
}
}
while (i <= last1)//对第一个子序列进行首尾处理
{
temp[k++] = data[i++];
}
while (j <= last2)//对第二个子序列进行首尾处理
{
temp[k++] = data[j++];
}
for (i = first1; i <= last2; i++)//边界是first1和last2 注意是i<=last2
{
data[i] = temp[i];//将合并数组传回数组data
}
delete[]temp;//堆区开辟空间需要释放
}
void Sort::MergeSort1(int first, int last)
{
if (first == last)//递归出口 只有一个记录
{
return;
}
else
{
int mid = (first + last) / 2;
MergeSort1(first, mid);//归并排序前半个子序列
MergeSort1(mid+1, last);//归并排序后半个子序列
Merge(first, mid, last);//将两个已排序的子序列合并
}
}
void Sort::MergeSort2()
{
int h = 1;
while (h < length)
{
MergePass(h);
h = 2 * h;
}
}
void Sort::MergePass(int h)
{
int i = 0;
while (i + 2 * h <= length)
{
Merge(i, i+h-1, i+2*h-1);
i = i + 2 * h;
}
if (i + h < length)
{
Merge(i, i + h-1, length-1);
}
}
Sort.cpp
#include "Sort.h"
int main()
{
int select, r[10] = { 2, 5, 7, 1, 9, 4, 3, 6, 5, 8 };
cout << "原数据是:";
for (int i = 0; i < 10; i++)
cout << r[i] << " ";
cout << endl;
Sort L(r, 10);
cout << "1. 直接插入排序 2. 希尔排序" << endl;
cout << "3. 起泡排序 4. 快速排序" << endl;
cout << "5. 简单选择排序 6. 堆排序" << endl;
cout << "7. 二路归并递归排序 8. 二路归并非递归排序" << endl;
cout << "请输入使用的排序技术编号:";
cin >> select;
switch (select)
{
case 1: L.InsertSort(); break;
case 2: L.ShellSort(); break;
case 3: L.BubbleSort(); break;
case 4: L.QuickSort(0, 9); break;
case 5: L.SelectSort(); break;
case 6: L.HeapSort(); break;
case 7: L.MergeSort1(0, 9); break;
case 8: L.MergeSort2(); break;
default: cout << "输入排序编号错误" << endl; break;
}
L.Print();
return 0;
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








