[Matlab]约束最小二乘解决力的最优化问题

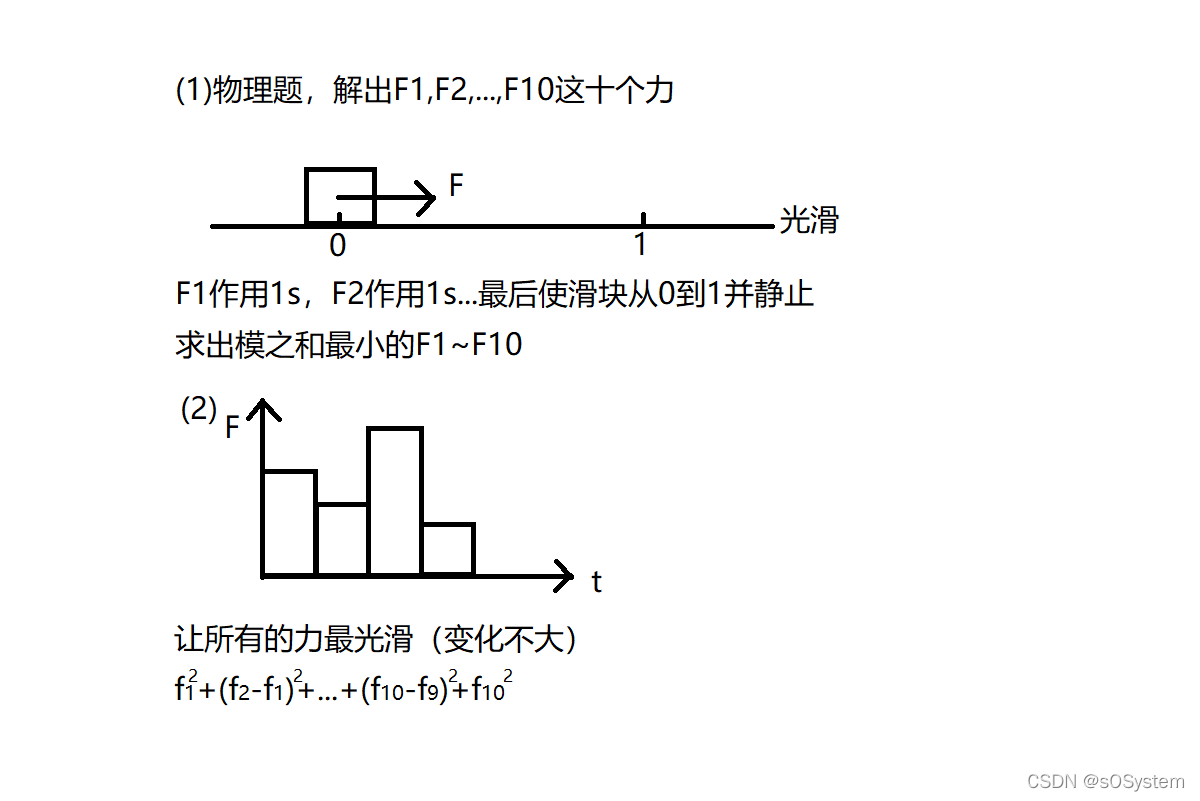
这一整道题是关于约束最小二乘(CLS constrained least squares)的问题。

推导

CLS要解决的问题是：

最小化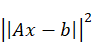           

约束于           

目标函数为

是约束条件

最后要找到的一定满足

我们要找到的满足于  并且对任何满足于  的n维向量x都满足

可以将约束最小二乘想象成加权最小二乘的特殊情况

这是上一个实验中给出的加权目标函数：

改变为：

的形式，而对于，将它视为无穷大，因此对于这个加权最小二乘问题，能够解决的办法就是

对于求解约束最小二乘问题，需要用到拉格朗日(Lagrange)乘数法。为了理解在矩阵中如何使用拉格朗日乘数法，我首先复习了一下高数里学到的用拉格朗日乘数法解决极值问题：

给定约束条件 ，求  的极值。

解决方法为：构造辅助函数  ，然后列出：

三个方程，三个未知数，解得x, y代入可以求得的极值。

拉格朗日乘数法的特点即，对于给定的n个不同的约束，使用n个不同的辅助变量，虽然最后我们并不需要这些辅助变量的值，但这些辅助变量时求解出极值的过程中所必要的。

将拉格朗日乘数法应用于矩阵计算当中

对于求 极值，约束条件为

利用拉格朗日乘数法，辅助变量取

分别对各变量求偏导

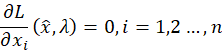
对于第二组的偏导

这个式子是已知的约束条件。

对于第一组的结果：

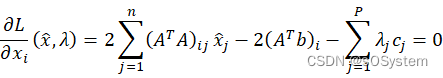
转换为矩阵的形式：

将该式子与  结合得到KKT矩阵(关于)：

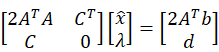
将等式左侧的左边的矩阵放到等式右侧

回到这个实验题目中，这个实验是一种特殊的约束最小二乘的情况。结果是求所有力的模的最小值，即，其中E是单位矩阵，0是0矩阵，即最后要求的结果为，其中为由所有力组成的矩阵。

将代入

得到

进一步简化为

从而推导出

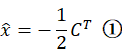
将②式代入①式中得：

其中是C的伪逆矩阵

(1)

根据题目条件构造C矩阵，利用加速度公式

==>

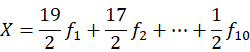
由此可以得出本题的约束条件为：

构造出的C矩阵为：

d矩阵为：

矩阵形式表示约束为：

代入公式

即可得到所求的力的矩阵

Matlab代码实现：

代码中 x_hat 为最终要求的10个力组成的矩阵，res为根据所求的10个力所求的模之和。

计算结果：

10个力分别为

该情况下模之和为0.0030

(2)

第2小问依然是 的特殊情况，解题思路和第1小问一样，不同的是需要改变用到的物理公式。这题要求的是变化力的模之和的最小值，解题时需要从用求最终速度和最终位移转换为用求最终的速度和最终的位移。

由于推到较为复杂，这里直接放了我的手写推导公式的过程：

每时刻的

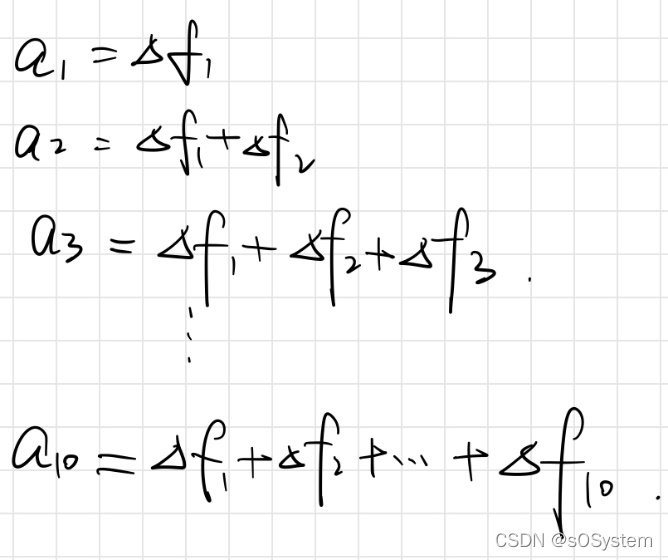
每时刻的v

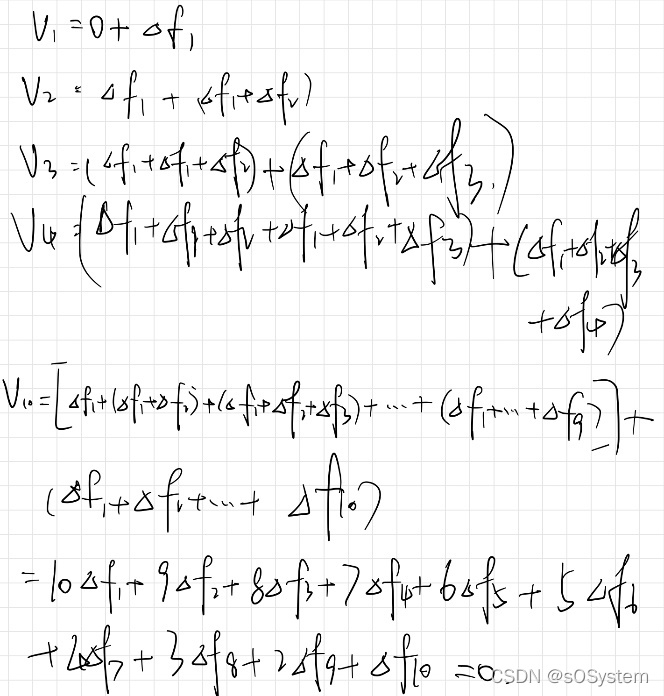
每时刻的位移x

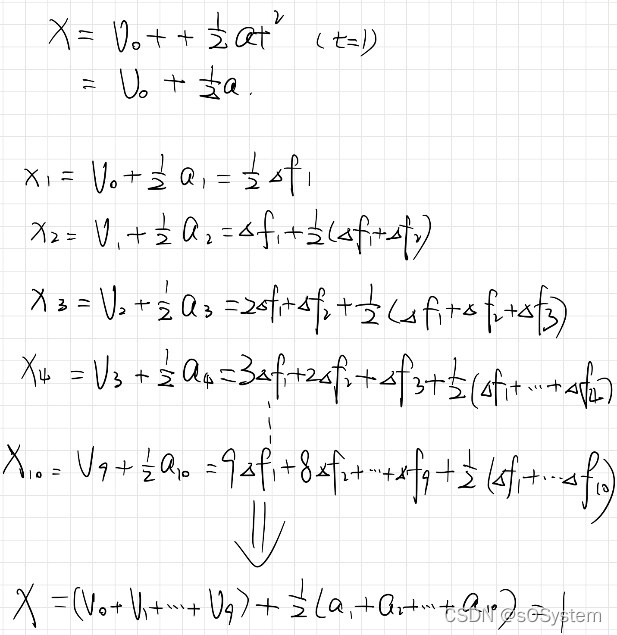
Matlab代码实现：

在Matlab中计算每时刻的a, v, x以及总的位移X

计算结果

因此矩阵为：

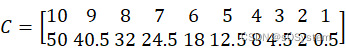
Matlab中的计算结果

这里用的是进行推导，因此最终约束条件为：

方便起见，还是直接代入推导出的公式

最终结果：

这个结果是每时刻的，即每时刻力的变化大小，转化为每时刻的：

计算结果

该情况下力的变化的模值

证明

至此该实验利用推导出的公式结合KKT条件计算出了两个小题，但是反推结果，为什么利用KKT矩阵公式求得x就是最终所需要的结果呢？

对于一般的情况，需求是最小化

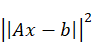
已知x是使得上式最小的结果，且满足约束

其中后项

用上文推导出的KKT矩阵

可以得出

将③代入②

又因为和都满足约束条件 ,即

因此可以得到

将④代回①中：

因此

显然满足于一开始提到的满足条件：

满足于  并且对任何满足于  的n维向量x都满足

因此是解决问题的最终结果。

参考资料

[1] Stanford Online. Constrained least squares https://youtu.be/vOFsja_YmJc