蓝桥杯官网练习题（九宫幻方）

题目描述

小明最近在教邻居家的小朋友小学奥数，而最近正好讲述到了三阶幻方这个部分，三阶幻方指的是将 1~9 不重复的填入一个 3*3 的矩阵当中，使得每一行、每一列和每一条对角线的和都是相同的。

三阶幻方又被称作九宫格，在小学奥数里有一句非常有名的口诀："二四为肩，六八为足，左三右七，戴九履一，五居其中"，通过这样的一句口诀就能够非常完美的构造出一个九宫格来。

4 9 2

3 5 7

8 1 6

有意思的是，所有的三阶幻方，都可以通过这样一个九宫格进行若干镜像和旋转操作之后得到。现在小明准备将一个三阶幻方（不一定是上图中的那个）中的一些数抹掉，交给邻居家的小朋友来进行还原，并且希望她能够判断出究竟是不是只有一个解。

而你呢，也被小明交付了同样的任务，但是不同的是，你需要写一个程序。

输入描述

输入仅包含单组测试数据。

每组测试数据为一个 3*3 的矩阵，其中为 0 的部分表示被小明抹去的部分。

给出的矩阵至少能还原出一组可行的三阶幻方。

输出描述

如果仅能还原出一组可行的三阶幻方，则将其输出，否则输出"Too Many"（不包含引号）。

输入输出样例

示例

输入

0 7 2
0 5 0
0 3 0

输出

6 7 2
1 5 9
8 3 4

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
  static int[] num=new int[10];
  static int[] ans=new int[10];
  static int[] biaoji=new int[10];
  static int m=0;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        for(int i=1;i<=9;i++){
          num[i]=scan.nextInt();
          biaoji[num[i]]=1;
        }
        dfs(1);
        if(m==1){
          System.out.printf(ans[1]+" "+ans[2]+" "+ans[3]+"\n");
          System.out.printf(ans[4]+" "+ans[5]+" "+ans[6]+"\n");
          System.out.printf(ans[7]+" "+ans[8]+" "+ans[9]+"\n");
        }
        else{
          System.out.println("Too Many");
        }
        scan.close();
    }
    public static void dfs(int n){
      if(n==10){
        int a=num[1]+num[2]+num[3];
        int b=num[4]+num[5]+num[6];
        int c=num[7]+num[8]+num[9];
        int d=num[1]+num[4]+num[7];
        int e=num[2]+num[5]+num[8];
        int f=num[3]+num[6]+num[9];
        int g=num[1]+num[5]+num[9];
        int h=num[3]+num[5]+num[7];
        if(a==b&&b==c&&c==d&&d==e&&e==f&&f==g&&g==h){
          for(int i=1;i<=9;i++){
            ans[i]=num[i];
          }
          m=1;
          return;
        }
        else{
          return;
        }
      }
      if(num[n]!=0){
        dfs(n+1);
      }
      for(int i=1;i<=9;i++){
        if(num[n]==0&&biaoji[i]==0){
          num[n]=i;
          biaoji[i]=1;
          dfs(n+1);
          num[n]=0;
          biaoji[i]=0;
        }
      }
    }
}

=========================================================================

类似：蓝桥杯官网填空题(七星填数)

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

如下图所示。在七角星的 1414 个节点上填入 11 ~ 1414的数字，不重复，不遗漏。 要求每条直线上的四个数字之和必须相等。

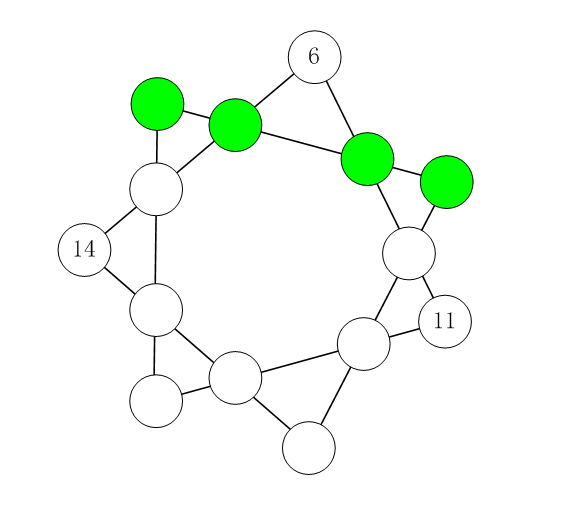
图中已经给出了 33 个数字。 请计算其它位置要填充的数字，答案唯一。

填好后，请输出绿色节点的 44 个数字（从左到右，用空格分开）。

运行限制

• 最大运行时间：1s
• 最大运行内存: 128M

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
  public static void main(String args[]){
  /* static int m=0;
     static int[] arr=new int[]{6,0,0,0,0,0,0,0,0,0,14,0,11,0};
     static int[] arr1=new int[15];
     static int[] ans=new int[15];
     public static void main(String[] args) {
         for(int i=0;i<14;i++){
             if(arr[i]!=0){
                 arr1[arr[i]]=1;
             }
         }
         dfs(0);
         if(m==1){
             System.out.printf(ans[1] + " " + ans[2] + " " + ans[3] + " " + ans[4]);
         }
     }
     public static void dfs(int n){
         if(n==14) {
             int a = arr[0] + arr[3] + arr[5] + arr[12];
             int b = arr[12] + arr[6] + arr[8] + arr[13];
             int c = arr[13] + arr[9] + arr[11] + arr[1];
             int d = arr[1] + arr[2] + arr[3] + arr[4];
             int e = arr[4] + arr[5] + arr[6] + arr[7];
             int f = arr[7] + arr[8] + arr[9] + arr[10];
             int g = arr[10] + arr[11] + arr[2] + arr[0];
             if (a == b && b == c && c == d && d == e && e == f && f == g) {
               for(int i=0;i<14;i++){
                 ans[i]=arr[i];
               }
                 m=1;
                 return;
             }
             else{
                 return;
             }
         }
         if(arr[n]!=0){
             dfs(n+1);
         }
         for(int i=1;i<=14;i++){
             if(arr1[i]==0&&arr[n]==0){
                 arr[n]=i;
                 arr1[i]=1;
                 dfs(n+1);
                 arr[n]=0;
                 arr1[i]=0;
             }
         }
     }  */
     System.out.println(10+" "+3+" "+9+" "+8);
  }
 }

=========================================================================

类似：蓝桥杯官网填空题（幻方填空）

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

幻方是把一些数字填写在方阵中，使得行、列、两条对角线的数字之和都相等。

欧洲最著名的幻方是德国数学家、画家迪勒创作的版画《忧郁》中给出的一个 44 阶幻方。

他把 1,2,3,...161,2,3,...16 这 1616 个数字填写在 4×44×4 的方格中。

如下图所示，即：

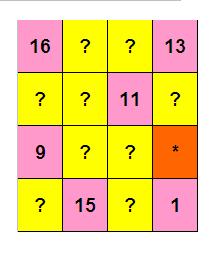
表中有些数字已经显露出来，还有些用 ? 和 ∗ 代替。

请你计算出 ? 和 ∗ 所代表的数字。并把 * 所代表的数字作为本题答案提交。

运行限制

• 最大运行时间：1s
• 最大运行内存: 128M

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
  static int[] ans = new int[16];
     static int flag = 0;
     static int[] a = new int[]{16, 0, 0, 13, 0, 0, 11, 0, 9, 0, 0, 0, 0, 15, 0, 1};
     static int[] biaoji = new int[17];

     public static void main(String[] args) {
         Scanner scan = new Scanner(System.in);
         for (int i = 0; i < 16; i++) {
             if (a[i] != 0) {
                 biaoji[a[i]] = 1;
             }
         }
         dfs(0);
         if (flag == 1) {
             System.out.println(ans[11]);
         }
         scan.close();
     }

     public static void dfs(int n) {
         if (n == 16) {
             int a1 = a[0] + a[1] + a[2] + a[3];
             int a2 = a[4] + a[5] + a[6] + a[7];
             int a3 = a[8] + a[9] + a[10] + a[11];
             int a4 = a[12] + a[13] + a[14] + a[15];
             int a5 = a[0] + a[4] + a[8] + a[12];
             int a6 = a[1] + a[5] + a[9] + a[13];
             int a7 = a[2] + a[6] + a[10] + a[14];
             int a8 = a[3] + a[7] + a[11] + a[15];
             int a9 = a[0] + a[5] + a[10] + a[15];
             int a10 = a[3] + a[6] + a[9] + a[12];
             if (a1 == a2 && a2 == a3 && a3 == a4 && a4 == a5 && a5 == a6 && a6 == a7 && a7 == a8 && a8 == a9 && a9 == a10) {
                 for (int i = 0; i < 16; i++) {
                     ans[i] = a[i];
                 }
                 flag = 1;
                 return;
             } else {
                 return;
             }
         }
         if (a[n] != 0) {
             dfs(n + 1);
         }
         for (int i = 1; i <= 16; i++) {
             if (a[n] == 0 && biaoji[i] == 0) {
                 a[n] = i;
                 biaoji[i] = 1;
                 dfs(n + 1);
                 a[n] = 0;
                 biaoji[i] = 0;
             }
         }
     }
 }