蓝桥杯官网练习题（剪格子）

原创已于 2023-08-07 14:20:27 修改 · 78 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#蓝桥杯 #算法 #职场和发展

于 2023-07-27 22:01:47 首次发布

该编程问题要求判断一个m×n的格子中的整数能否被分割成两部分，使得两部分的数字和相等。给定格子的大小及各单元格的整数值，使用深度优先搜索（DFS）算法来寻找可能的分割，目标是最小化包含左上角格子的区域的大小。如果无法分割，则输出0。

题目描述

如下图所示，3 x 3 的格子中填写了一些整数。

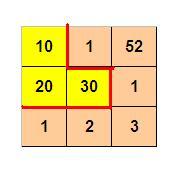
我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是 60。

本题的要求就是请你编程判定：对给定的 m×n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。

如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。

如果无法分割，则输出 0。

输入描述

程序先读入两个整数 m,n 用空格分割 (m,n<10)，表示表格的宽度和高度。

接下来是 n 行，每行 m 个正整数，用空格分开。每个整数不大于10的4次方。

输出描述

在所有解中，包含左上角的分割区可能包含的最小的格子数目。

输入输出样例

示例

输入

输出

运行限制

最大运行时间：5s
最大运行内存: 64M

import java.util.*;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    static Scanner scan = new Scanner(System.in);
    static int m=scan.nextInt();
    static int n=scan.nextInt();
    static int[] dx=new int[]{1,-1,0,0};
    static int[] dy=new int[]{0,0,1,-1};
    static int sum=0;
    static int[][] a=new int[n][m];
    static int min=Integer.MAX_VALUE;
    static int[][] biaoji=new int[n][m];

    public static void main(String[] args) {
        //在此输入您的代码...
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                a[i][j]=scan.nextInt();
                sum=sum+a[i][j];
            }
        }
        dfs(0,0,0,0);
        System.out.println(min);
        scan.close();
    }

    public static void dfs(int i,int j,int gezi,int ans){
        int nx=0,ny=0;
        if(ans==sum/2){
            min=Math.min(gezi,min);
            return;
        }
        if(i>=0&&j>=0&&i<n&&j<m&&ans<sum/2&&biaoji[i][j]==0){
            biaoji[i][j]=1;
            ans=ans+a[i][j];
            for(int k=0;k<dx.length;k++){
                nx=i+dx[k];
                ny=j+dy[k];
                dfs(nx,ny,gezi+1,ans);
            }
            biaoji[i][j]=0;
        }
    }
}