Elmo

Elmo

1 Elmo简介

ELMo是一种新型深度语境化词表征，可对词进行复杂特征(如句法和语义)和词在语言语境中的变化进行建模(即对多义词进行建模)。词向量是深度双向语言模型(biLM)内部状态的函数，在一个大型文本语料库中预训练而成。

2 Elmo原理

模型架构图如下：

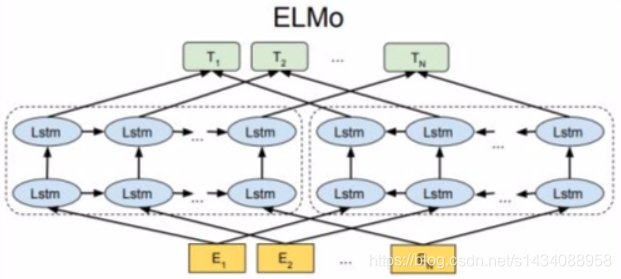
2.1 LSTM

Elmo的基本由LSTM构成 首先理解下何为LSTM
LSTM网络引入一个新的内部状态（internal state）$c_t$ 专门进行
线性的循环信息传递，同时（非线性）输出信息给隐藏层的外部状态$h_t$。
$$c_t=f_t⨀c_t-1+i_t⨀c_t^{\prime }$$
$$h_t=o_t⨀tanh(c_t)$$
其中$f_t，i_t$ 和$o_t$ 为三个门（gate）来控制信息传递的路径；⊙为向量元素乘积；
$c_{t-1}$ 为上一时刻的记忆单元；$c_t^{\prime }$ 是通过非线性函数得到候选状态

在数字电路中，门（Gate）为一个二值变量{0, 1}，0代表关闭状态，不许
任何信息通过；1代表开放状态，允许所有信息通过。

LSTM网络中的“门”是一种“软”门，取值在(0, 1)之间，表示以一定的比例运行信息通过。
LSTM网络中三个门的作用为

• 遗忘门$f_t$ 控制上一个时刻的内部状态$c_{t-1}$ 需要遗忘多少信息。

• 输入门$i_t$ 控制当前时刻的候选状态$c_t^{\prime }$ 有多少信息需要保存。

• 输出门$o_t$控制当前时刻的内部状态$c_t$有多少信息需要输出给外部状态$h_t$。

当$f_t=0,i_t=1$时，记忆单元将历史信息清空，并将候选状态向量$c_t^{\prime }$ 写入。

但此时记忆单元$c_t$ 依然和上一时刻的历史信息相关。

当$f_t=1,i_t=0$时，记忆单元将复制上一时刻的内容，不写入新的信息。

三个门的计算方式为：

$$i_t=\sigma (W_i{x}_t+U_i{h}_{t-1}+b_i)$$
$$f_t=\sigma (W_f{x}_t+U_f{h}_{t-1}+b_f)$$
$$o_t=\sigma (W_o{x}_t+U_o{h}_{t-1}+b_o)$$

其中$\sigma (x)$为Logistic函数，其输出区间为(0, 1)，$x_t$ 为当前时刻的输入，$h_{t-1}$ 为
上一时刻的外部状态。

下图给出了 LSTM 网络的循环单元结构，其计算过程为：

（1）首先利用上一时刻的外部状态$h_{t-1}$ 和当前时刻的输入$x_t$，计算出三个门，以及候选状态
$c_t^{\prime }$；

（2）结合遗忘门$f_t$ 和输入门$i_t$ 来更新记忆单元$c_t$；

（3）结合输出门$o_t$，将内部状态的信息传递给外部状态$h_t$。

循环神经网络中的隐状态h存储了历史信息，可以看作是一种记忆（Memory）。

在简单循环网络中，隐状态每个时刻都会被重写，因此可以看作是一种短期记忆（Short-Term Memory）。

在神经网络中，长期记忆（Long-Term Memory）可以看作是网络参数
，隐含了从训练数据中学到的经验，并更新周期要远远慢于短期记忆。

而在LSTM网络中，记忆单元c可以在某个时刻捕捉到某个关键信息，
并有能力将此关键信息保存一定的时间间隔。

记忆单元c中保存信息的生命周期要长于短期记忆h，但又远远短于长期记忆，
因此称为长的短期记忆（Long Short-Term Memory）。

2.2 Elmo的双向LSTM模型

2.2.1 前向模型

给定一串长度为N的词条$(t_1,t_2,\dots ,t_N)$，前向语言模型通过对给定历史$(t_1,\dots t_{k-1})$预测$t_k$进行建模
$$p\left(t_1,t_2,\dots ,t_N\right)=\prod _{k=1}^{N}p\left(t_k|t_1,t_2,\dots ,t_{k-1}\right)$$
第一步：将单词转换成了n*1的列向量，进行word embedding，得到 LSTM的输入 $x_t$。

第二步：将上一时刻的输出/隐状态$h_{k-1}$及第一步中的 $x_t$送入lstm，

并得到输出及隐状态$h_k$。其中，隐状态$h_k$是一个m*1的列向量。

第三步：将lstm的输出$h_k$，与上下文矩阵$W$相乘，即$W{h}_k$得到一个列向量，再将该列向量经过softmax归一化。其中，假定数据集有V个单词，$W$是$|V|\ast m$的矩阵，$h_k$是$m\ast 1$的列向量，于是最终结果是$|V|\ast 1$的归一化后向量，即从输入单词得到的针对每个单词的概率。

2.2.2 双向模型

对于多层lstm，每层的输出都是1.1节中提到的隐向量$h_t$，在ELMo里，为了区分，前向lstm语言模型的第j层第k时刻的输出向量命名为$h_{k,j}^{L,M\to }$ 。

对于后向语言模型，跟前向语言模型类似，除了它是给定后文来预测前文。
$$p\left(t_1,t_2,\dots ,t_N\right)=\prod _{k=1}^{N}p\left(t_k|t_{k+1},t_{k+2},\dots ,t_N\right)$$

类似的，设定后向lstm的第j层的第k时刻的输出向量命名为$h_{k,j}^{L,M\leftarrow }$。

前向、后向lstm语言模型所要学习的目标函数。elmo使用的双向lstm语言模型，论文中简称biLM。作者将前后向公式结合起来，得到所要优化的目标：最大化对数前向和后向的似然概率。
$$\begin{array}{l}{\sum }_{k=1}^N(\log p\left(t_k|t_1,\dots ,t_{k-1};{\Theta }_x,\vec{\Theta }LSTM,\Theta s\right)\\ +\log p\left(t_k|t_{k+1},\dots ,t_N;{\Theta }_x,\overleftarrow{\Theta }LSTM,\Theta s\right))\end{array}$$

2.2.3 Elmo模型

Elmo就是把输入$x_k^{L,M}$，前向输出$h_{k,j}^{L,M,\to }$ ，后向输出$h_{k,j}^{L,M\leftarrow }$ 结合起来
$$\begin{gathered} R_k=(x_k^{L,M},h_{k,j}^{L,M,\to },h_{k,j}^{L,M\leftarrow }|j=1,...,L) \\ =(h_{k,j}^{L,M}|j=0,...,L) \end{gathered}$$

1.最简单的方法就是使用最顶层的lstm输出
2.对于每层向量，加一个权重$s_j^{task}$，将每层的向量与权重相乘，然后再乘以一个权重$\gamma$。对于每一个$token$，一个L层的biLM要计算出共$2L+1$个表征。
$$ELM{o}_k^{\text{ task }}=E\left(R_k;{\Theta }^{\text{ task }}\right)={\gamma }^{\text{ task }}\sum _{j=0}^L{s}_j^{\text{ task }}{\mathbf{h}}_{k,j}^{LM}$$

3 训练

论文的作者有预训练好的ELMo模型，映射层（单词到word embedding）使用的Jozefowicz的CNN-BIG-LSTM[5]，即输入为512维的列向量。同时LSTM的层数L，最终使用的是2，即L=2。每层的LSTM的单元数是4096。每个LSTM的输出也是512维列向量。每层LSTM（含前、向后向两个）的单元个数是4096个（从1.1节可以知公式4m2 = 4512*2 = 4096）。也就是每层的单个lstm的输入是512维，输出也是512维。

一旦模型预训练完成，便可以用于nlp其他任务。在一些领域，可以对biLM（双向lstm语言模型）进行微调，对任务的表现会有所提高，这种可以认为是一种迁移学习（transfer learning）

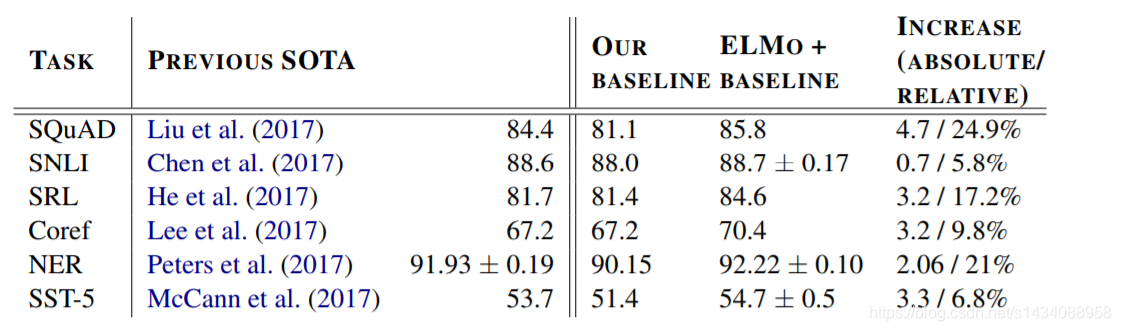
4 模型效果

对于诸多NLP任务 Elmo有少许提升 其中SQuAD 提升4.7%
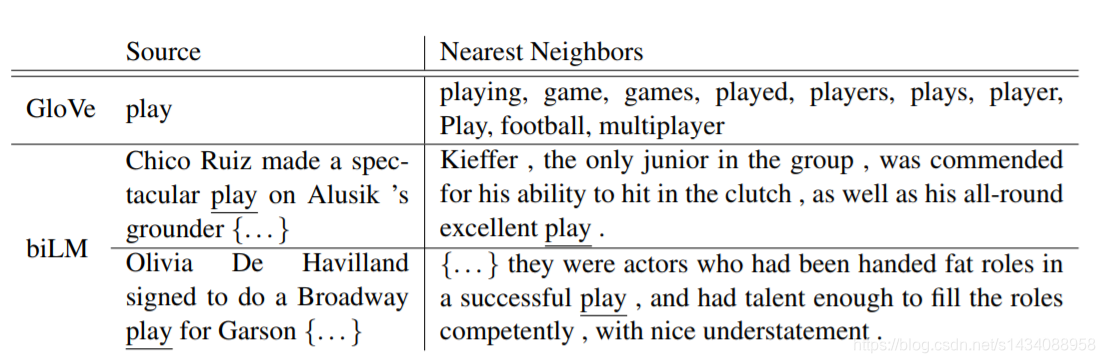
对于多义词不同语义的学习

参考 :
[1]: Peters, Matthew E., et al. “Deep contextualized word representations.” arXiv preprint arXiv:1802.05365 (2018)
[2] :https://zhuanlan.zhihu.com/p/51679783