计算机博弈之国际跳棋入门-棋子可行招搜索

最新推荐文章于 2024-07-12 21:58:09 发布

0x5A52

最新推荐文章于 2024-07-12 21:58:09 发布

阅读量1.7k

点赞数 8

CC 4.0 BY-SA版权

分类专栏：人工智能计算机博弈

本文链接：https://blog.youkuaiyun.com/rzhengbj163/article/details/97797876

人工智能同时被 2 个专栏收录

11 篇文章

订阅专栏

计算机博弈

5 篇文章

订阅专栏

本文详细介绍跳棋AI招法生成的基本思路与实例分析，包括兵与王的可行招法生成，通过具体实例展示了如何利用栈和队列数据结构实现招法搜索与回溯，最终确定合法招法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、基本思路

实现计算机博弈程序需要解决的基础问题之一是生成可行招法，不同的棋类根据规则的不同，生成可行招的方法也有所不同。以围棋为例，可行招的判断要解决哪里放置己方棋子的问题，其核心在于判断空位是否已经被对手棋子所围，因为自杀是不可以的，以及是否违反其它禁手规则。而对于国际跳棋，根据其行棋规则，需要先对每个可走的棋子判断其所有可能的走法，找到该棋子吃子最多的走法，作为候选招法，所有候选招法再进行比较，吃子最多的为可行招，这是根据“有吃必吃，有吃多吃”的规则。而可走的棋子可能为兵，也可能为王，在搜索可能的走法时要考虑其差异，最后还应注意不能违反“不得重吃跳吃”的规则。

如果能将每个棋子的候选招法生成，不同的棋子只需要比较候选招法吃掉棋子的数目即可以得到本次行棋的可行招法。对于每个棋子，首先要判断当前可以行棋的走法，这里实际上可以将王和兵统一考虑，只是对于王来说需要判断其所处的两条交叉直线上所有可以行棋的位置，需要判断的情况多一些，每次搜索到可以吃子的走法，我们就将其保存下来，逐个选择这些走法，并通过将吃掉的棋子标记，来完成当前这个走法，完成当前这个走法后又可以重复上述过程，继续搜索可以吃子的走法，如果搜索不到可以吃子的走法，我们首先将当前跳过的位置保存到某个数组或其它数据结构以待将来比较，然后将吃掉的子标记为没吃掉，回跳到上一个跳点继续完成其它没有搜索过的吃子的走法，重复上述过程直至回到原始位置，这个过程可以通过两个具体例子分析进行理解，在纸上首先记下整个搜索的过程，然后再考虑用程序如何实现这个功能。

二、实例分析

例1：如图所示为一不含王的对弈局面，此时轮到白棋行棋，根据前述搜索思路，具体过程如下：从上自下，从左至右，依次对12、18、41、42四枚白色棋子分别统计候选招法。

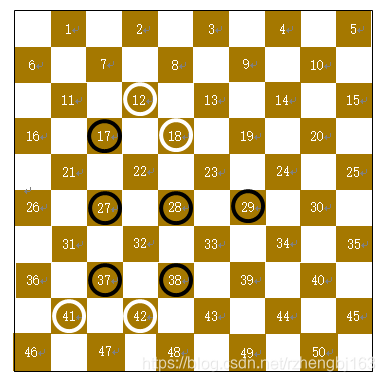
【棋子12】

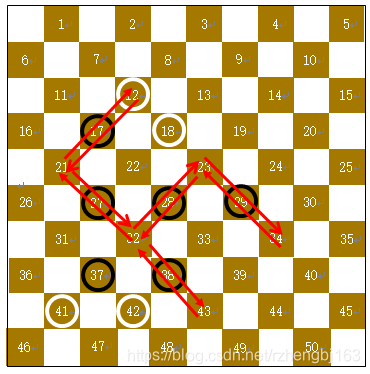
详细步骤

步骤序号	当前步骤执行内容	候选招法	已吃子标记
1	可行走法为7,8和跳吃17至21，由于“有吃必吃”，因此执行跳吃走法至21	12->21	17
2	在21处可跳吃至12、跳吃至32，由于跳吃至12需要吃掉已经被标记的17子，因此可行走法只有吃掉27跳至32	12->21->32	17,27
3	在32处可跳吃至21、跳吃至23、跳吃至43，由于27已经被标记，因此只有跳吃至23和跳吃至43可行，将两个都记录，并选择跳吃至23执行	12->21->32->23	17,27,28
4	在23处可跳吃至32，跳吃至34，由于28已经被标记，因此只有跳吃至34可行	12->21->32->23->34	17,27,28,29
5	在34处可跳吃至23，但29已经被标记，因此此时已经没有可行走法，已完成一个完整的招法，与候选招法中的招法比较，当前招法为唯一招法，因此只记录	【12->21->32->23->34】 12->21->32->23->34	17,27,28,29
6	由于34处已经没有可行走法，开始回溯，回溯到23，并取消相应吃子标记	【12->21->32->23->34】 12->21->32->23	17,27,28
7	在23处检查是否还有已记录的走法未被执行，没有找到，继续回溯到32，并取消相应吃子标记	【12->21->32->23->34】 12->21->32	17,27
8	在32处检查是否还有已记录的走法未被执行，发现跳吃至43未被执行，选择执行，标记38被吃	【12->21->32->23->34】 12->21->32->43	17,27,38
9	在43处可跳吃至32，但38已经被标记，因此此时已经没有可行走法，完成一个完整招法，与候选招法中的招法比较，因为步数小于已保存的候选招法，因此不对候选招法进行改动	【12->21->32->23->34】 12->21->32->43	17,27,38
10	由于43处已经没有可行走法，开始回溯，回溯到32，并取消相应吃子标记	【12->21->32->23->34】 12->21->32	17,27
11	在32处没有已记录的走法未被执行，继续回溯至21，取消相应吃子标记	【12->21->32->23->34】 12->21	17
12	在21处没有已记录的走法未被执行，继续回溯至12，取消相应吃子标记	【12->21->32->23->34】 12	空
13	在12处没有已记录的走法未被执行，亦已不可以回溯，对棋子12的候选招法搜索执行完毕	【12->21->32->23->34】	空

【棋子18】

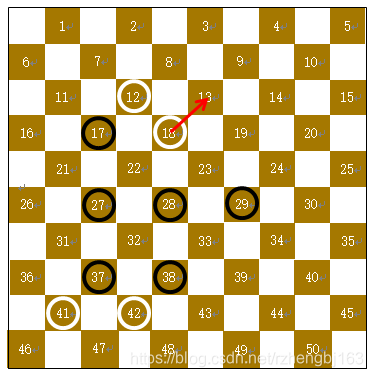
详细步骤

步骤序号	当前步骤执行内容	候选招法	已吃子标记
1	只有一步可行走法为13	行至13	空

【棋子41】

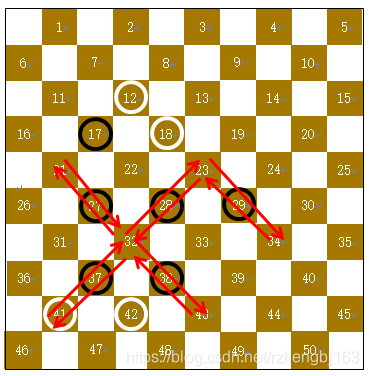
详细步骤

步骤序号	当前步骤执行内容	候选招法	已吃子标记
1	可行走法为36和跳吃37至32，由于“有吃必吃”，因此执行跳吃走法至32	41->32	37
2	在32处可跳吃至21、跳吃至23、跳吃至41、跳吃至43，由于跳吃至41需要吃掉已经被标记的37子，因此可行走法为三个，选择吃掉棋子27跳至21执行	41->32->21	37,27
3	在21处可跳吃至32但27已经被标记，因此此时已经没有可行走法，已完成一个完整的招法，当前招法为唯一招法，因此只记录	【41->32->21】 41->32->21	37,27
4	由于21处已经没有可行走法，开始回溯，回溯到32，并取消相应吃子标记	【41->32->21】 41->32	37
5	在32处发现还有未被执行的走法，选择执行未被执行的走法跳吃至23，标记棋子28为已吃	【41->32->21】 41->32->23	37,28
6	在23处只有一步跳吃29至34可走，执行该走法	【41->32->21】 41->32->23->34	37,28,29
7	在34处已经没有可行走法，已完成一个完整的招法，当前招法的步数大于已保存的招法，因此替换招法为当前招法	【41->32->23->34】 41->32->23->34	37,28,29
8	由于34处已经没有可行走法，开始回溯，回溯到23，并取消相应吃子标记	【41->32->23->34】 41->32->23	37,28
9	由于23处已经没有可行走法，开始回溯，回溯到32，并取消相应吃子标记	【41->32->23->34】 41->32	37
10	在32处发现还有未被执行的走法，选择执行未被执行的走法跳吃至43，标记棋子38为已吃	【41->32->23->34】 41->32->43	37,38
11	在43处已经没有可行走法，已完成一个完整的招法，当前招法的步数小于已保存的招法，因此不修改	【41->32->23->34】 41->32->43	37,38
12	由于43处已经不已经没有可行走法，开始回溯，回溯到32，并取消相应吃子标记	【41->32->23->34】 41->32	37
13	在32处没有已记录的走法未被执行，继续回溯至41，取消相应吃子标记	【41->32->23->34】 41	空
14	在41处没有已记录的走法未被执行，亦已不可以回溯，对棋子41的候选招法搜索执行完毕	【41->32->23->34】	空

【棋子42-1】（分成两部分）

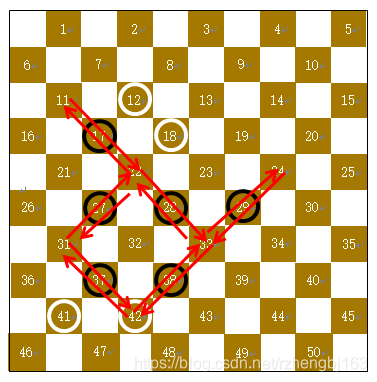
详细步骤（1-15）

步骤序号	当前步骤执行内容	候选招法	已吃子标记
1	可行走法为跳吃37至31和跳吃38至33，先选择吃掉37至31	42->31	37
2	在31处只可跳吃27至22	42->31->22	37,27
3	在22处，可以跳吃17至11也可跳吃28至33，选择跳吃17至11	42->31->22->11	37,27,17
4	在11处已经没有可行走法，已完成一个完整的招法，当前招法为唯一招法，将其保存	【42->31->22->11】 42->31->22->11	37,27,17
5	由于11处已经没有可行走法，开始回溯，回溯到22，并取消相应吃子标记	【42->31->22->11】 42->31->22	37,27
6	在22处选择执行另一可行走法跳吃28至33	【42->31->22->11】 42->31->22->33	37,27,28
7	在33处存在跳吃29至24和跳吃38到42两种走法，先选择跳吃29到24	【42->31->22->11】 42->31->22->33->24	37,27,28,29
8	在24处已经没有可行走法，已完成一个完整的招法，当前招法的步数大于已保存的招法，因此替换招法为当前招法	【42->31->22->33->24】 42->31->22->33->24	37,27,28,29
9	由于24处已经没有可行走法，开始回溯，回溯到33，并取消相应吃子标记	【42->31->22->33->24】 42->31->22->33	37,27,28
10	在33处还有跳吃38到42未执行，选择执行	【42->31->22->33->24】 42->31->22->33->42	37,27,28,38
11	在42处已经没有可行走法，已完成一个完整的招法，当前招法的步数与已保存的招法相同，因此当前招法加入候选招法	【42->31->22->33->24】【42->31->22->33->42】 42->31->22->33->42	37,27,28,38
12	由于42处已经没有可行走法，开始回溯，回溯到33，并取消相应吃子标记	【42->31->22->33->24】【42->31->22->33->42】 42->31->22->33	37,27,28
13	在33处已经没有可行走法，开始回溯，回溯到33，并取消相应吃子标记	【42->31->22->33->24】【42->31->22->33->42】 42->31->22->33	37,27,28
14	在22处已经没有可行走法，开始回溯，回溯到31，并取消相应吃子标记	【42->31->22->33->24】【42->31->22->33->42】 42->31	37
15	在31处已经没有可行走法，开始回溯，回溯到42，并取消相应吃子标记	【42->31->22->33->24】【42->31->22->33->42】 42	空

【棋子42-2】（分成两部分）

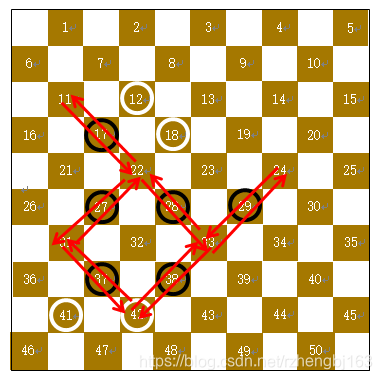
详细步骤（16-31）

16	在42处有跳吃38至33未执行，执行跳吃38至33	【42->31->22->33->24】【42->31->22->33->42】 42->33	38
17	在33处有跳吃28至22和跳吃29至24两种走法，先选择跳吃28至22	【42->31->22->33->24】【42->31->22->33->42】 42->33->22	38,28
18	在22处有跳吃17至11和跳吃27至31两种走法，先选择跳吃17至11	【42->31->22->33->24】【42->31->22->33->42】 42->33->22->11	38,28,17
19	在11处已经没有可行走法，已完成一个完整的招法，当前招法的步数小于已保存的招法，因此不对候选招法修改	【42->31->22->33->24】【42->31->22->33->42】 42->33->22->11	38,28,17
20	由于11处已经没有可行走法，开始回溯，回溯到22，并取消相应吃子标记	【42->31->22->33->24】【42->31->22->33->42】 42->33->22	38,28
21	在22处选择剩余的可行走法跳吃27至31	【42->31->22->33->24】【42->31->22->33->42】 42->33->22->31	38,28,27
22	在31处选择可行走法跳吃37至42	【42->31->22->33->24】【42->31->22->33->42】 42->33->22->31->42	38,28,27,37
23	在42处已经没有可行走法，已完成一个完整的招法，当前招法的步数等于已保存招法步数，因此加入候选招法	【42->31->22->33->24】【42->31->22->33->42】【42->33->22->31->42】 42->33->22->31->42	38,28,27,37
24	由于42处已经没有可行走法，开始回溯，回溯到31，并取消相应吃子标记	【42->31->22->33->24】【42->31->22->33->42】【42->33->22->31->42】 42->33->22->31	38,28,27
25	由于31处已经没有可行走法，开始回溯，回溯到22，并取消相应吃子标记	【42->31->22->33->24】【42->31->22->33->42】【42->33->22->31->42】 42->33->22	38,28
26	由于22处已经没有可行走法，开始回溯，回溯到33，并取消相应吃子标记	【42->31->22->33->24】【42->31->22->33->42】【42->33->22->31->42】 42->33	38
27	在33处选择另一走法跳吃29至24	【42->31->22->33->24】【42->31->22->33->42】【42->33->22->31->42】 42->33->24	38,29
28	在24处已经没有可行走法，已完成一个完整的招法，当前招法的步数小于已保存的招法，因此不对候选招法修改	【42->31->22->33->24】【42->31->22->33->42】【42->33->22->31->42】 42->33->24	38,29
29	由于24处已经没有可行走法，开始回溯，回溯到33，并取消相应吃子标记	【42->31->22->33->24】【42->31->22->33->42】【42->33->22->31->42】 42->33	38
30	由于33处已经没有可行走法，开始回溯，回溯到42，并取消相应吃子标记	【42->31->22->33->24】【42->31->22->33->42】【42->33->22->31->42】 42	空
31	在42处没有已记录的走法未被执行，亦已不可以回溯，对棋子42的候选招法搜索执行完毕	【42->31->22->33->24】【42->31->22->33->42】【42->33->22->31->42】	空

综上，通过对棋子12、18、41、42的候选招法分析，可知当前白方可选合法招法为按照招法【41->32->23->34】移动41子，或按照招法【42->31->22->33->24】【42->31->22->33->42】【42->33->22->31->42】中的任何一个移动42子，共有四种合法招法。

例2：如图所示为一含王的对弈局面，此时轮到白棋行棋，根据前述搜索思路，具体过程如下：从上自下，从左至右，依次对8、18、29、37、41五枚白色棋子分别统计候选招法，其中白棋8为王。兵的搜索候选招方法通过例1中已经进行了详细解释，因此在本例中不再赘述18、39、37、41的候选招，显然它们吃子最多不超过2。下面主要分析8号棋位上王的候选招法。由于在王的招法搜索中重复路线过多，因此用王可能落棋的各节点将路径分成短线段连接。

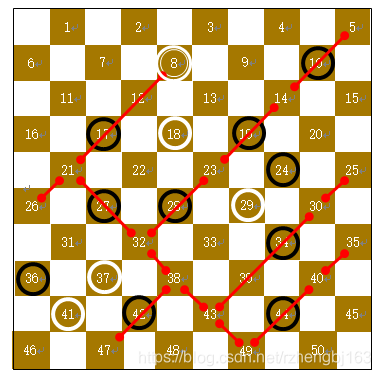
详细步骤

步骤序号	当前步骤执行内容	候选招法	已吃子标记
1	8位王的可行走法是跳吃17至21或26两种走法，首先选择跳吃17至21	8->21	17
2	在21处的可行走法是跳27吃至32,38,43,49首先选择跳吃至32	8->21->32	17,27
3	在32处的可行走法是跳吃28至23	8->21->32->23	17,27,28
4	在23处的可行走法是跳吃19至14	8->21->32->23->14	17,27,28,19
5	在14处的可行走法是跳吃10至5	8->21->32->23->14->5	17,27,28,19,10
6	在5处无可行走法，完成了一个可行招法，候选招法为空，因此保存至候选招法	【8->21->32->23->14->5】 8->21->32->23->14->5	17,27,28,19,10
7	在5处无可行走法，回溯至14，取消吃子标记	【8->21->32->23->14->5】 8->21->32->23->14	17,27,28,19
8	在14处无可行走法，回溯至23，取消吃子标记	【8->21->32->23->14->5】 8->21->32->23	17,27,28
9	在23处无可行走法，回溯至32，取消吃子标记	【8->21->32->23->14->5】 8->21->32	17,27
10	在32处无可行走法，回溯至21，取消吃子标记	【8->21->32->23->14->5】 8->21	17
11	在21处选择未走过的38，同样是跳吃27	【8->21->32->23->14->5】 8->21->38	17,27
12	在38处的可行走法是跳吃42至47	【8->21->32->23->14->5】 8->21->38->47	17,27,42
13	在47处无可行走法，完成一个可行招法，与候选招法比较，步数小于候选招法，因此不修改候选招法	【8->21->32->23->14->5】 8->21->38->47	17,27,42
14	在47处无可行走法，回溯至38，取消吃子标记	【8->21->32->23->14->5】 8->21->38	17,27
15	在38处无可行走法，回溯至21，取消吃子标记	【8->21->32->23->14->5】 8->21	17
16	在21处选择未走过的43，同样是跳吃27	【8->21->32->23->14->5】 8->21->43	17,27
17	在43处的可行走法是跳吃34至30或25，先选择吃至30	【8->21->32->23->14->5】 8->21->43->30	17,27,34
18	在30处无可行走法，完成一个可行招法，与候选招法比较，步数小于候选招法，因此不修改候选招法	【8->21->32->23->14->5】 8->21->43->30	17,27,34
19	在30处无可行走法，回溯至43，取消吃子标记	【8->21->32->23->14->5】 8->21->43	17,27
20	在43处的选择另一可行走法是跳吃34至25	【8->21->32->23->14->5】 8->21->43->25	17,27,34
21	在25处无可行走法，完成一个可行招法，与候选招法比较，步数小于候选招法，因此不修改候选招法	【8->21->32->23->14->5】 8->21->43->25	17,27,34
22	在25处无可行走法，回溯至43，取消吃子标记	【8->21->32->23->14->5】 8->21->43	17,27
23	在43处无可行走法，回溯至21，取消吃子标记	【8->21->32->23->14->5】 8->21	17
24	在21处选择未走过的49，同样是跳吃27	【8->21->32->23->14->5】 8->21->49	17,27
25	在49处的可行走法是跳吃44至40或35，先选择吃至40	【8->21->32->23->14->5】 8->21->49->40	17,27,44
26	在40处无可行走法，完成一个可行招法，与候选招法比较，步数小于候选招法，因此不修改候选招法	【8->21->32->23->14->5】 8->21->49->40	17,27,44
27	在40处无可行走法，回溯至49，取消吃子标记	【8->21->32->23->14->5】 8->21->49	17,27
28	在49处的选择另一可行走法跳吃44至35	【8->21->32->23->14->5】 8->21->49->35	17,27,44
29	在35处无可行走法，完成一个可行招法，与候选招法比较，步数小于候选招法，因此不修改候选招法	【8->21->32->23->14->5】 8->21->49->35	17,27,44
30	在35处无可行走法，回溯至49，取消吃子标记	【8->21->32->23->14->5】 8->21->49	17,27
31	在49处无可行走法，回溯至21，取消吃子标记	【8->21->32->23->14->5】 8->21	17
32	在21处无可行走法，回溯至8，取消吃子标记	【8->21->32->23->14->5】 8	空
33	在8处还有跳吃17至26可走	【8->21->32->23->14->5】 8->26	17
34	在26处无可行走法，完成一个可行招法，与候选招法比较，步数小于候选招法，因此不修改候选招法	【8->21->32->23->14->5】 8->26	17
35	在35处无可行走法，回溯至8，取消吃子标记	【8->21->32->23->14->5】 8-	空
36	在8处没有已记录的走法未被执行，亦已不可以回溯，对王棋8的候选招法搜索执行完毕	【8->21->32->23->14->5】	空

三、程序实现（伪代码+C/C++代码）

从具体实例的分析我们能够看出，实际上王棋和兵棋的走法在结构上是可以统一的，只是在统计每个节点的可行走法上，王棋比兵棋复杂。另外要实现回溯，最合理的方法就是采用数据结构中的栈来实现，需要申请栈变量存储可行走法。另外我们需要单独申请一个用于保存候选招法的变量，可以用队列来实现，队列的每个元素又是一个节点编号的队列用以表示招法。最后为了对已吃子进行标记，我们还需要申请一个变量，显然用一个和棋盘格大小一致的二维数组就可以实现这一点。在明确了上述任务之后，我们用伪代码来实现可行招搜索的功能，具体如下，代码采用了C/C++风格。

//假设当前己方棋子为白棋，为白棋搜索可行代码
//定义数据类型
Node //节点用坐标定义
{
   x; //横坐标
   y; //纵坐标
}

//走法数据类型，由起始点和终止点两个节点构成
//ndeat是要吃掉的子
//对于兵，要吃掉的子一定是起始点和终止点的中点
//对于王，要吃掉的子再起始点和终止点的连线上
NodeStep
{
   Node ndstt; //起点
   Node ndend; //终点
   Node ndeat; //吃子
}

Stack<NodeStep>  StepStack;   //走法栈
queue<NodeStep>  StepQueue;   //走法队列
queue<StepQueue> QStepQueue;  //走法队列的队列，用于保存候选招法或是移动走法

//这里的分析只针对吃子，nd为要分析的节点
bool AnalyseNode(Node nd，StepStack stacktmp)
{
   //hasfound为二值变量，为真表示找到了对于当前节点的吃子走法
   bool hasfound=假；

   //这两个数组可用于标示方位
   xd={-1,1,-1,1};
   yd={-1,-1,1,1};

   NodeStep ndstep;

   if(ChessArray[x][y]等于白兵)
    {
      //分别对左上，右上，左下，右下判断，如果可吃子，压入节点栈
      for(i=0;i<4;i++)
      {
         if((x+2*xd[i])>-1 并且 (x+2*xd[i])<10 并且 (y+2*yd[i])>-1 并且 (y+2*yd[i])<10) 
         {
            if(ChessArray[x+2*xd[i]][y+2*yd[i]]为空 并且 ChessArray[x+xd[i]][y+yd[i]]为黑兵或黑王 并且 HoldArray[x+xd[i]][y+yd[i]]为假)
            {
               ndstep.ndstt.x=x;
               ndstep.ndstt.y=y;

               ndstep.ndend.x=x+2*xd[i];
               ndstep.ndend.y=y+2*yd[i];

               ndstep.ndeat.x=x+xd[i];
               ndstep.ndeat.y=y+yd[i];

               stacktmp.push(ndstep);
               hasfound=真；
            }
         }      
      }
   }
   else if(ChessArray[x][y]等于白王)
   {
      Node ndtmp; 
      //分别对左上，右上，左下，右下判断，如果可吃子，压入走法栈
      for(i=0;i<4;i++)
      {
         ndtmp.x=x;
         ndtmp.y=y;

         定义二值状态变量 canloc表示是否可以落子；
         canloc初始化为假；

         ndstep.ndstt.x=x;
         ndstep.ndstt.y=y;

         //先跳过空格
         while(ndtmp.x>-1 并且 ndtmp.x<10 并且 ndtmp.y>-1 并且 nttmp.y<10)
         {
            ndtmp.x += xd[i];
            nttmp.y += yd[i];

            if ChessArray[ndtmp.x][ndtmp.y]为空
               继续循环;
            if ChessArray[ndtmp.x][ndtmp.y]为白兵或白王
               退出循环；
            if ChessArray[ndtmp.x][ndtmp.y]为黑兵或黑王,并且HoldArray[ndtmp.x][ndtmp.y]为假，执行如下操作：
                  ndstep.ndeat.x = ndtmp.x;
                  ndstep.ndeat.y = ndtmp.y;
                  canloc=真；
                  ndtmp.x+=xd[i],ndtmp.y+=yd[i];
               退出循环；
         }

         if(canloc)
         {
            //在跳过对方一个棋子后，所有空格都是可行步，如果其后的棋子不为空或者
            //超出边界，不会将该走法压入走法栈
            while(ndtmp.x>-1 并且 ndtmp.x<10 并且 ndtmp.y>-1 并且 nttmp.y<10)
            {
               if ChessArray[ndtmp.x][ndtmp.y]为空，执行如下操作
                  ndstep.ndend.x = ndtmp.x;
                  ndstep.ndend.y = ndtmp.y;

                  stacktmp.push(ndstep);
                  hasfound=真；

                  ndtmp.x += xd[i];
                  nttmp.y += yd[i];
               else
                  退出循环
            }
         }
      }
   }

   返回 hasfound
}

//主函数
int main()
{
   QNodeQueue ways_move, ways_eat; //保存候选招法和移动走法的变量

   NOArray[10][10];             //常量二维数组, 其中和棋盘格对应坐标存储的是编号1到50
   ChessArray[10][10];          //棋子数据，其中保存五种类型的值：白兵、白王、黑兵、黑王、空
   HoldArray[10][10];           //吃子状态二维数组，二值数组，只能有真和假两个状态

   StepStack  stepwait;         //未完成走法栈
   StepQueue  stepfinish;       //已完成走法队列

   HoldArray[10][10] = {0}；    //将吃子状态置为全FALSE

   Node  nodecur;               //定义当前节点变量

   NodeStep stepcur;            //定义当前走法

   For(x=0; x<10; x++)
   {
      For(y=0; y<10; y++)
      {
         if(ChessArray[x][y]等于白兵或白王)
         {
            //为根节点赋值
            nodecur.x = x;
            nodecur.y = y;
            //清空栈
            stepwait.empty();
            stepfinish.empty();

            //分析可行走法，如果存在吃子走法，将当前可行吃子走法压入stepwait
            //首先判断吃子走法，因为如果候选招法不为空的话，根据有吃必吃，没有必要搜索移动的走法
            while(true)
            {
               if(AnalyseNode(nodecur, stepwait)为真)
               {
                  //从未走走法栈中选择一个执行，并将走到的节点处走法压入未走走法栈
                  stepcur = stepwait.pop();
                  //已被执行的走法，相应吃子位置为真，存入已完成走法队列
                  HoldArray[stepcur.ndeat.x][stepcur.ndeat.y]=真；
                  stepfinish.push_back(stepcur);
                  //节点更新为走法的终点位置
                  nodecur = stepcur.ndend;
               }
               else
               {
                  //如果当前节点不存在可行走法，首先判定当前的已完成走法队列长度
                  //是否超过候选招法
                  如果ways_eat中的走法队列长度小于stepfinish，清空ways_eat中的
                  走法队列，将stepfinish存入，如果ways_eat中的走法队列长度等于
                  stepfinish，将stepfinish加入ways_eat
                  
                  //回溯至stepwait中的可行走法
                  while(stepfinish.IsNotEmpty())
                  {
                     stepcur =  stepfinish.pop_back();
                     HoldArray[stepcur.ndeat.x][stepcur.ndeat.y]=假；
                     //找到分支走法
                     如果stepwait不为空 并且 stepcur的ndstt与stepwait顶部step的ndstt相等
                     执行如下代码
                        stepcur = stepwait.pop();
                        HoldArray[stepcur.ndeat.x][stepcur.ndeat.y]=真；
                        stepfinish.push_back(stepcur);
                        nodecur = stepcur.ndend;
                  } 

                  if(spstackwait.IsEmpty()并且spstackfinish.IsEmpty())
                     退出循环；
               }
            }
         }
      }
   }

   if(ways_eat为空)
   {
       对棋盘上己方可移动子进行遍历，由于移动的步法不存在比较，因此检索到的结果全部存入ways_move 
   }
}