算法笔记（十六）—— 有序表（红黑树，AVL树，Size-balance树，跳表），一文搞定！

有序表所有的操作都是O(logN)级别（红黑树，AVL树，Size-balance树，跳表）。

 红黑树，AVL树，Size-balance树都属于平衡搜索二叉树（BST）。

搜索二叉书（不保证平衡性）：

添：小的加在左边，大的加在右边

删除：在寻找结点时，记录其父结点

        1.  如果删除节点是叶子节点，直接删除

        2. 若有一个孩子，将孩子替代它的位子即可

        3. 如果左右孩子双全，拿左树上最右结点来替换，或者右树上的最左孩子来替换

AVL树（通过左旋右旋完成自平衡操作）

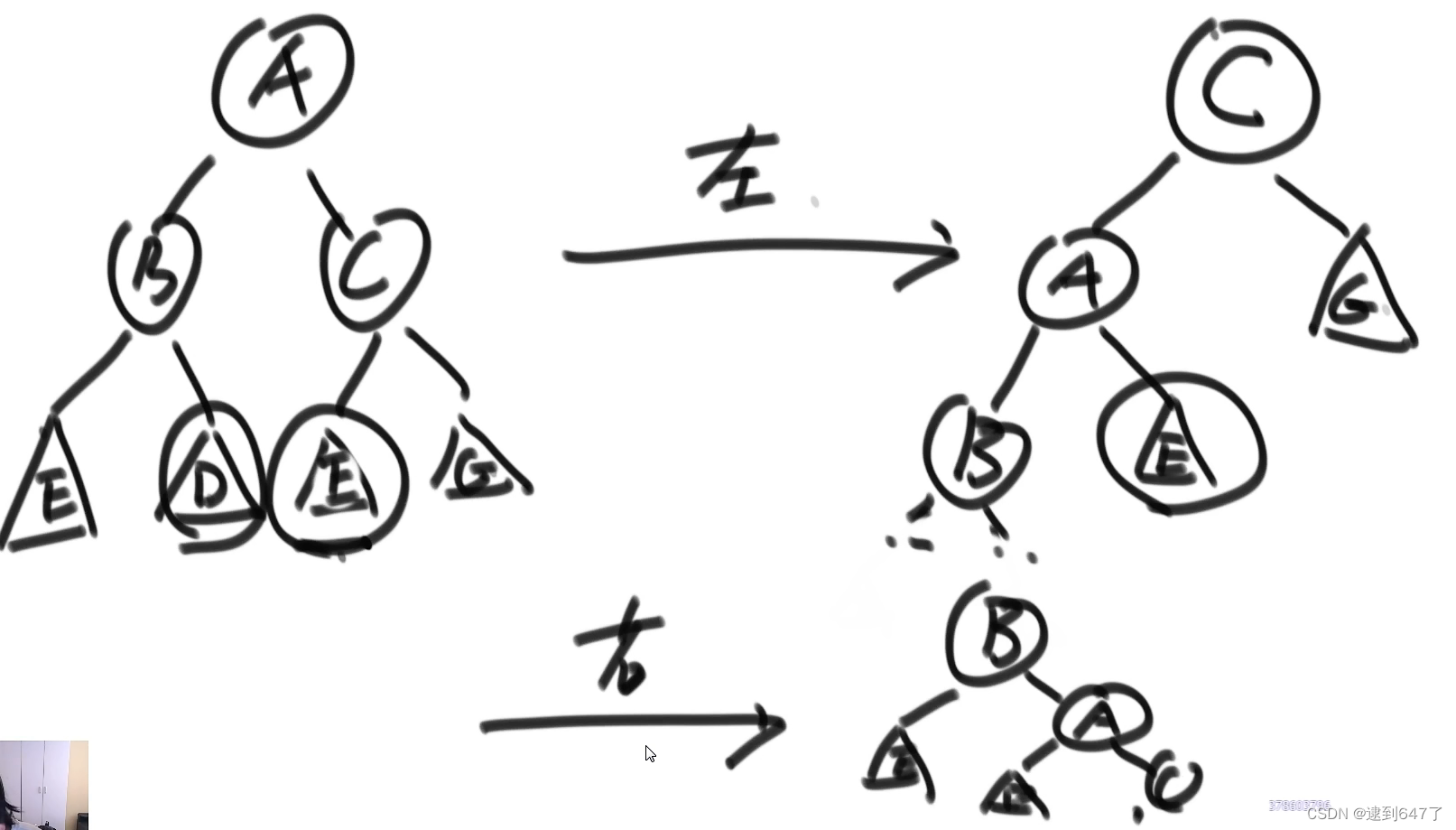
 检查不平衡的时机：

在添加节点，会沿着父节点路径检查节点有无平衡性

删除节点后，沿着被删除节点或替代节点的父结点路径检查

LL型：右旋即可

RR型：左旋即可

LR型（左子树的右子树过长）：左旋加右旋让左树的右树根节点成为整棵树的右节点

RL型：右旋加左旋

如何确定类型：右节点高度和左结点高度（nullptr当做-1），高度差不超过1

红黑树和size-balance树与AVL树在平衡性的判断不同，但调整操纵完全相同。

SB树（每棵叔叔树的大小不能小于侄子树的大小）

LL型（左孩子的左子树大小比右子树大）：右旋，然后对孩子节点变化的节点继续进行操作。

LR型（左孩子的右子树大小比右子树大）：将左孩子右子树根节点左旋右旋到达整棵树的根节点，对孩子节点变化的节点继续进行操作。

红黑树

1. 每个节点不是红就是黑

2. 头节点和叶子节点（最底层的空节点） 必须为黑

3. 任何两个红节点不能相邻

4. 任何一棵子树，从头部出发，到结束要求路径上的黑结点一样（最长的路和最短的路不会超过两倍）

跳表（最底层上，所有节点都存在）

1. 存在一个默认节点，拥有最小的key

2. 用户给我数据，封装成节点，我进行随机选择来决定该节点有几条往外指的指针（层数）

3. 根据新节点的层数来对默认节点进行扩充

4. 从高层开始，在本层内找到刚刚小于该数据的节点

        4.1 找到了，但该数据没有这么高的层数，降层

        4.2 找到了，并且该数据有这么高的层数，加在所找节点之前       

        4.3 若没找直接指向数据。

查找：从高层出发，不能往右走了过后往下走

删除：找到点，将其前节点和后节点连起来即可