贝叶斯理论-优快云博客

文章介绍了贝叶斯定理的基本概念，包括先验概率和后验概率，以及它们在概率和似然之间的区别。通过实例解释了如何利用贝叶斯定理更新知识，特别是在分类问题中的应用。朴素贝叶斯算法被提及，强调其在处理独立特征的分类任务中的使用，同时指出了该方法的优缺点。

参考：(6条消息) 贝叶斯、先验概率后验概率_贝叶斯先验概率和后验概率_王蒟蒻的博客-优快云博客

区分概率和似然：

概率直接描述随机事件,可以从数据频率估计：事先已经知道了所有样本的分布情况，在此基础上进行概率的计算

M个,白球N个，随手抓起一个球，求是黑球的概率

似然是给定参数下数据的概率,通过优化似然可以估计参数：不知道所有样本的信息，只能基于给定的信息

一个袋子中装着若干小球，里面有黑色跟白色，我们随机取出一些小球，然后根据小球的情况去计算袋中小球实际的分布情况

两者在机器学习中扮演不同的角色,概率表示数据分布,似然用于学习模型参数

运用场景：用于特征相互独立的分类问题

优缺点：

优点：

1. 算法逻辑简单,易于实现
2. 分类过程中时空开销小
缺点：

1. 特征间的相互独立难以保证，导致分类效果不好
2. 只适用于特征较少的情况

n维特征 $_{_{_{}}}$ $_{x_1,x_2,...x_n}$ 相互独立的，y有k个类别

1 根据条件概率公式

$P(A|B) = \frac{P(B|A) * P(A)}{P(B)}$

$P({y_k}|x) = \frac{{P(x|{y_k}) \times P({y_k})}}{{\sum\limits_k {P(x|{y_k}) \times P({y_k})} }}$

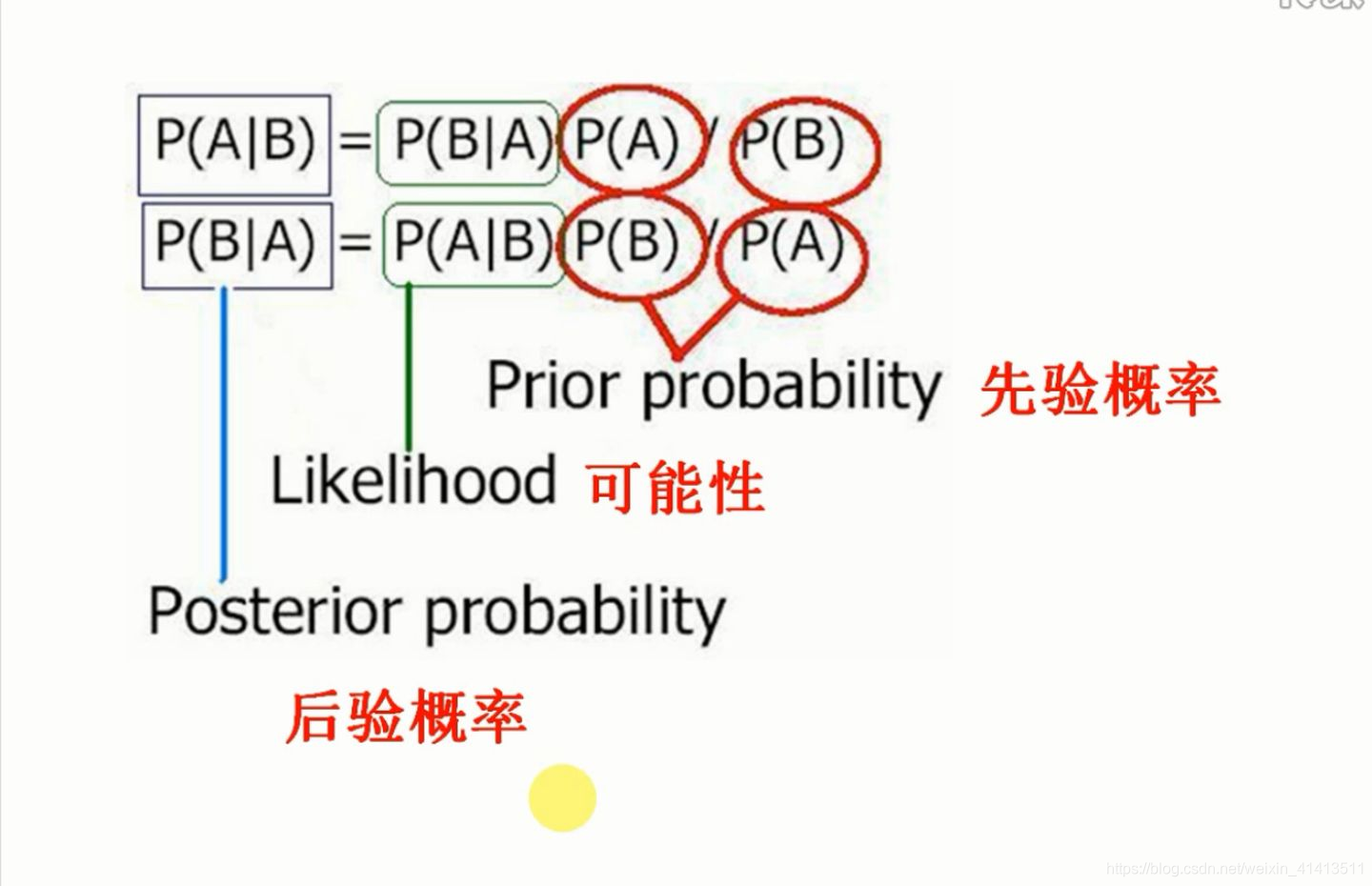
在这里插入图片描述

2 解释性

由先验概率Prior probability 和可能性 Likelihood 推出后验概率 Posterior probability，本质上是：

例：在全局事件中，遇到十字路口的概率仅仅为5%，但当看见前面的车打右转灯后，遇到十字路口的概率应该更新为95%。

通俗来讲，我想知道A事件的发生，如果没有任何的先验知识，我只能做出它发生与不发生的概率各占50%的判断。但是，幸运的是我知道B事件发生了，根据两者的关联经验，我知道它对A事件的发生起到促进作用，所以我可以更加准确的判断A事件是大概率发生的（如80%），而不是起初的非零即一的50%。如果我有更多A的关联事件，那么我可以做出更加准确的判断，这就是贝叶斯推断

先验概率 $P(y_k)$ : 样本为k类别的概率,根据以往经验和分析得到的概率

后验概率 $P(y_k|x) = P(y_k|x_1,x_2...x_n)$ : 当事件发生时，样本为k类别的概率

$\mathop {\arg \max }\limits_{{y_k}} P({y_k}|x)$ 后验概率最大的类别

3 推导公式【多变量】

$P(y_k|x_1,x_2...x_n) = \frac{P(x_1,x_2...x_n|y_k) * P(y_k)}{P(x_1,x_2,...x_n)}$

变量间相互独立时：

$P(x_1,x_2...x_n|y_k) = P(x_1|y_k) * P(x_2|y_k) * ...P(x_n|y_k) = \prod_{i=1}^{n}P(x_i|y_k)$

全概率公式

$P(x_1,x_2...x_n) =\sum^{k}_{1} P(x_1,x_2...x_n|y_k) * P(y_k)$

替换

$P({y_k}|x) = \frac{{P({y_k}) \times \prod\limits_{i = 1}^n {P({x_i}|{y_k})} }}{{\sum\limits_k {P({y_k}) \times \prod\limits_{i = 1}^n {P({x_i}|{y_k})} } }}$

$f(x) = \mathop {\arg \max }\limits_{{y_k}} P({y_k}|x) = \mathop {\arg \max }\limits_{{y_k}} \frac{{P({y_k}) \times \prod\limits_{i = 1}^n {P({x_i}|{y_k})} }}{{\sum\limits_k {P({y_k}) \times \prod\limits_{i = 1}^n {P({x_i}|{y_k})} } }}$