排序章总结-优快云博客

本文链接：https://blog.youkuaiyun.com/ruyuemoliang/article/details/143425144

这里插入一张常见排序算法的思维导图：

一.插入排序

⑴直接插入排序

时间复杂度 O（N^2）

根据动图我们可以很好的理解插入排序，就是往一个有序的排列中插入一个数。在数组中就是已排序序的后一个与前面的排列进行比较，排列中比它大的就往后挪，剩下的空位就填入该值。

代码实现如下：

//直接插入
void InsertSort(int* a, int n) {
	//[0，end]中插入end+1
	for (int i = 0; i < n-1; i++) {
		int end = i;
		int tem = a[end + 1];
		while (end >= 0) {
			if (tem <a[end]) {
				a[end + 1] = a[end];
			}
			else {
				break;
			}
			end--;
		}
		a[end + 1] = tem;

	}
}

⑵希尔排序（预排序＋直接插入排序）

时间复杂度 O（N^1.3）

希尔排序是一个时间复杂度大约在O（N^1.3）的排序算法，它的本质就是运用直接插入排序，所以在分类的时候将它划分在插入排序中。

它的排序可以分成2步

1.预排序分为gap组进行排序

2.当gap=1是就是采用了直接插入排序

希尔排序是直接插入排序的升级版，我们都知道直接插入排序的步长是1，即数据是一步一步移动的，这样的效率十分缓慢，尤其是在数据量很大的时候，这里对直接插入排序进行优化，将步长设置为gap，这样设计后数据移动的步长变大，大的数以更快的速度移到后面。

代码实现：

void ShellSort(int* a, int n) {
	int gap = n;

	while (gap > 1) {
		gap = gap / 3 + 1;
		for (int i = 0; i < gap; i++) {//一个gap的全过程
			for (int j = i; j < n - gap; j += gap) {//一个指定的gap的单趟
				int end = j;
				int tem = a[end + gap];
				while (end >= 0) {
					if (tem < a[end]) {
						a[end + gap] = a[end];
					}
					else {
						break;
					}
					end -= gap;
				}
				a[end + gap] = tem;



			}

		}
	}
}

//希尔
void ShellSort2(int* a, int n) {
	int gap = n;
	while (gap > 1) {
		gap = gap / 3 + 1;
		//一个gap的全过程
			for (int j = 0; j < n - gap; j++) {
				int end = j;
				int tem = a[end + gap];
				while (end >= 0) {
					if (tem < a[end]) {
						a[end + gap] = a[end];
					}
					else {
						break;
					}
					end -= gap;
				}
				a[end + gap] = tem;

			}
		}
	}

这两种是等价的，区别只是使用3个和2个循环，效率并没有提高。

二.选择排序

⑴选择排序

时间复杂度 O（N^2）

在一个排序中，一次遍历找出最大和最小分别排在头和尾，，再遍历一次找出次大和次小的排在相应的位置，重复几次，直到排序结束。

代码实现：

//选择排序
void selectSort(int* a, int n) {//一次性选出最大值和最小值，要注意特殊情况
	int max, min;
	int begin = 0;
	int end = n - 1;
	while (begin < end) {
		max = min = begin;
		for (int i = begin+1; i <= end; i++) {
			
			if (a[i] > a[max]) {
				max = i;
			}
			if (a[i] < a[min]) {
				min = i;
			}
		}
		Swap(&a[min], &a[begin]);
		if (max == begin) {
			max = min;
		}
		Swap(&a[max], &a[end]);
		begin++;
		end--;

	}
}

在进行选择排序的时候要注意一种特殊情况要变换下标，有时最大值刚好在排序起点的位置，或者最小值刚好在排序终点的位置，具体如何要看排序如何实现。

⑵堆排序

时间复杂度 O（N^logN）

在进行堆排序时，我们第一步要做的事情就是建堆，堆分为大堆和小堆，当我们要排升序时我们要建大堆，当我们排降序时我们要建小堆。建完堆后我们要进行排序，以降序为例，当我们建立了大堆后，根节点上的值就是最大值，此时我们将根节点与最后一个叶子结点进行交换，抛出开已经排好序的那个叶子结点，将堆重新调整为大堆，往复操作。

向下调整建堆的时间复杂度是O（N），而向上调整建堆的时间复杂度为O（N*logN）这里以向下调整建堆代码实现如下：


//堆排（向下调整）（调整一次O（logN））
void AdjustDown(int* a, int n, int parent) {
	int child = parent * 2 + 1;
	
	while (child<n) {
		if (child + 1 < n && a[child + 1] > a[child]) {
			child++;
		}
		if (a[child] > a[parent]) {
			Swap(&a[child], &a[parent]);
		}
		else {
			break;
		}
		parent = child;
		child = child * 2 + 1;
		
	}

}
void StackSort(int* a, int n) {

	int parent = (n-1 - 1) / 2;
	while (parent>=0) {
		AdjustDown(a, n, parent);//向下调整建堆（时间复杂度O（N））
		parent--;
	}
	int count = n-1;
	while (count>0) {
		Swap(&a[0], &a[count]);//时间复杂度O（N*log(N)）
		AdjustDown(a, count, 0);
		count--;

	}
	

}

三.交换排序

⑴冒泡排序

时间复杂度 O（N^2）

从头开始比较大小，将大的值交换到后面。

代码如下：

//冒泡
void BubbleSort(int* a, int n) {
	int fag = 0;
	for (int i = 1; i < n; i++) {
		
		for (int j = 0; j < n - i ; j++) {
			if (a[j] > a[j + 1]) {
				Swap(&a[j], &a[j + 1]);
				fag = 1;
			}
		}
		if (fag == 0) {
			break;
		}
	}

}

⑵快速排序

时间复杂度 O（N^logN）[快排最好的情况下为O（N*logN）,快排最坏的情况下为O（N*N），平均下来为O（N*logN）]

①快排单趟排序

要了解一个排序，就要了解这个排序的单趟。单趟排序的内核是一样的，选出一个数作为key将比它小的数甩到前面，将比它大的数甩在后面，这样key这个数就排好序了。快排单趟有3个版本实现，分别为hoare版本，挖坑法，前后指针法，本质都是为key排好序。

ⅰ霍尔版本（单趟）

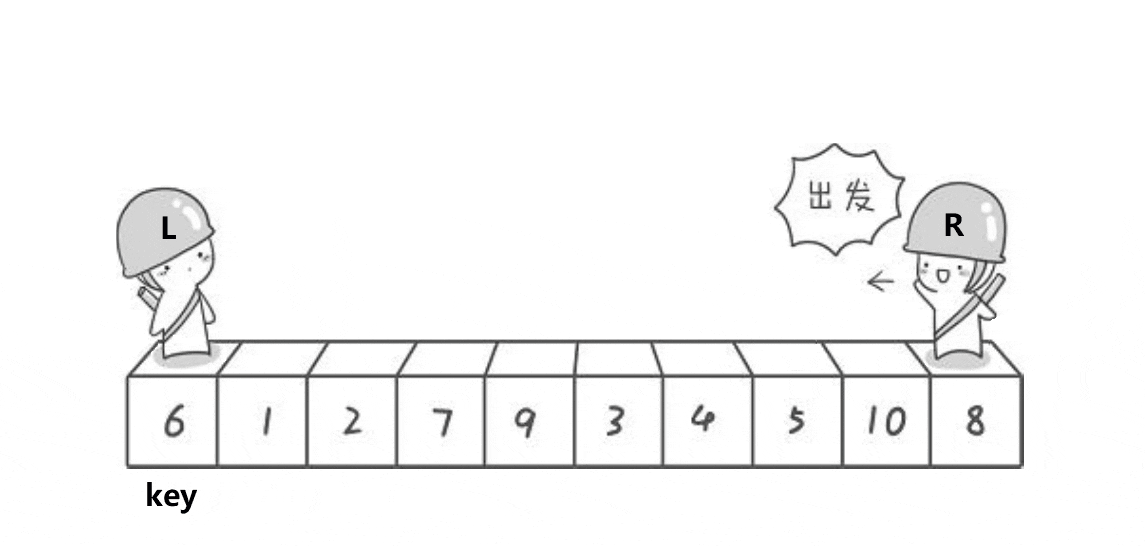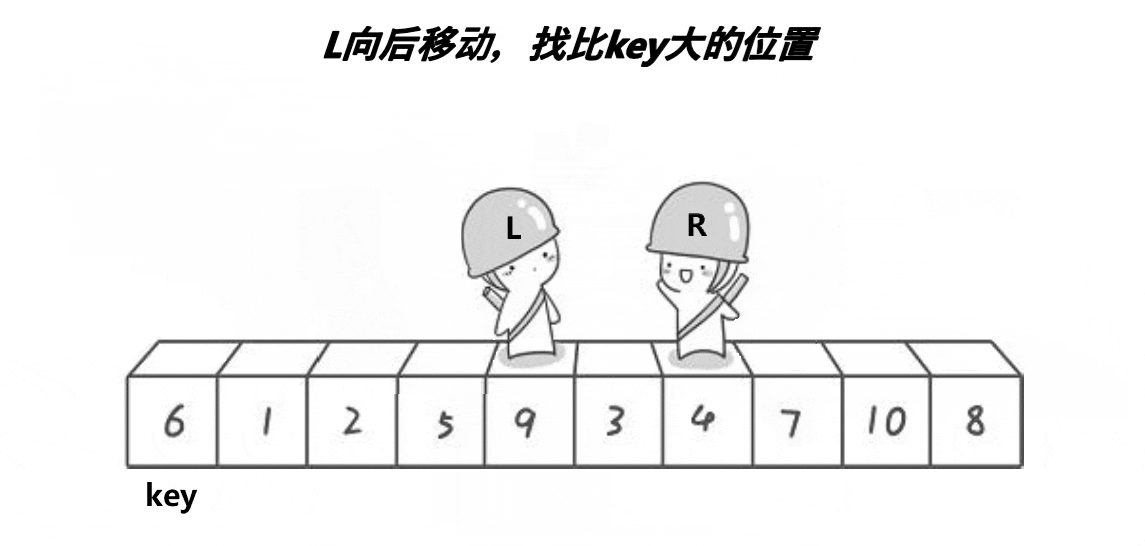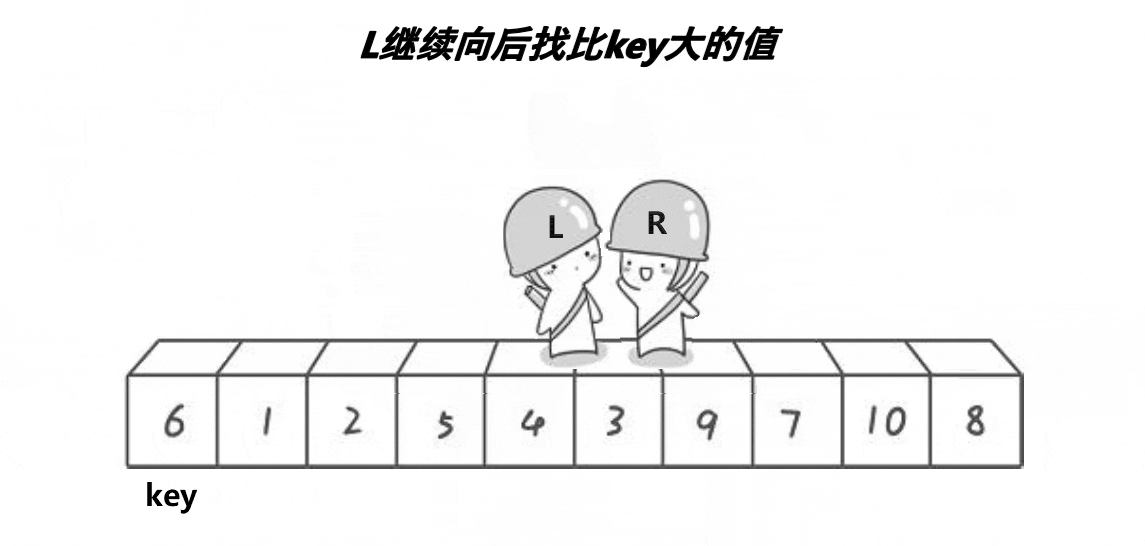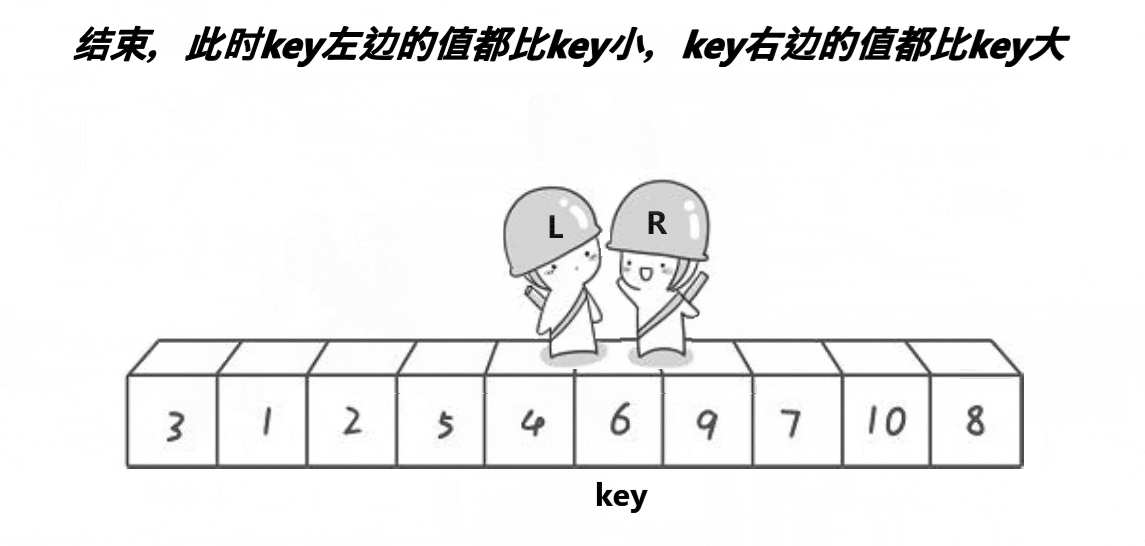
代码实现如下：

//快排单趟排序(霍尔)
int qsort1(int* a, int left, int right) {
	int begin = left;
	int end = right;
	
	//右边找小，左边找大
	
		while (begin < end) {
			while (begin < end && a[end] >= a[keyi]) {
				end--;
			}
			while (begin < end && a[begin] <= a[keyi]) {
				begin++;
			}

			Swap(&a[begin], &a[end]);
		}
		Swap(&a[begin], &a[keyi]);
		return begin;
	}

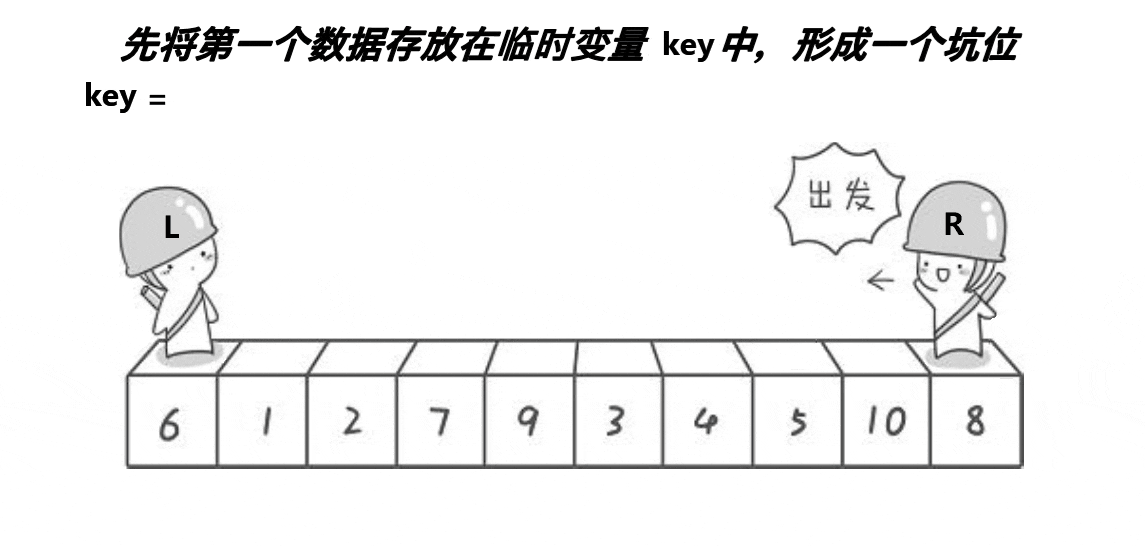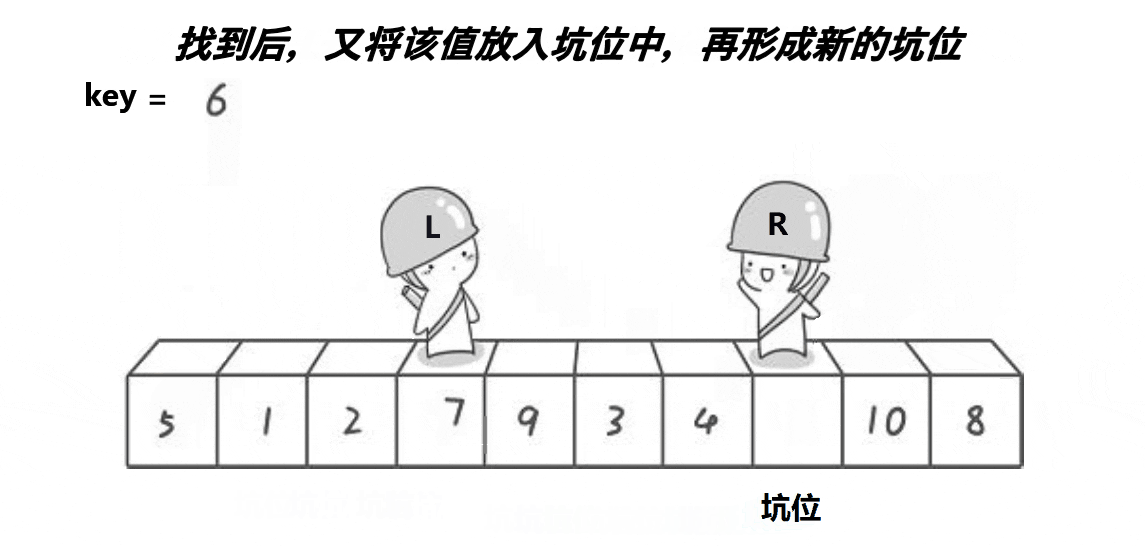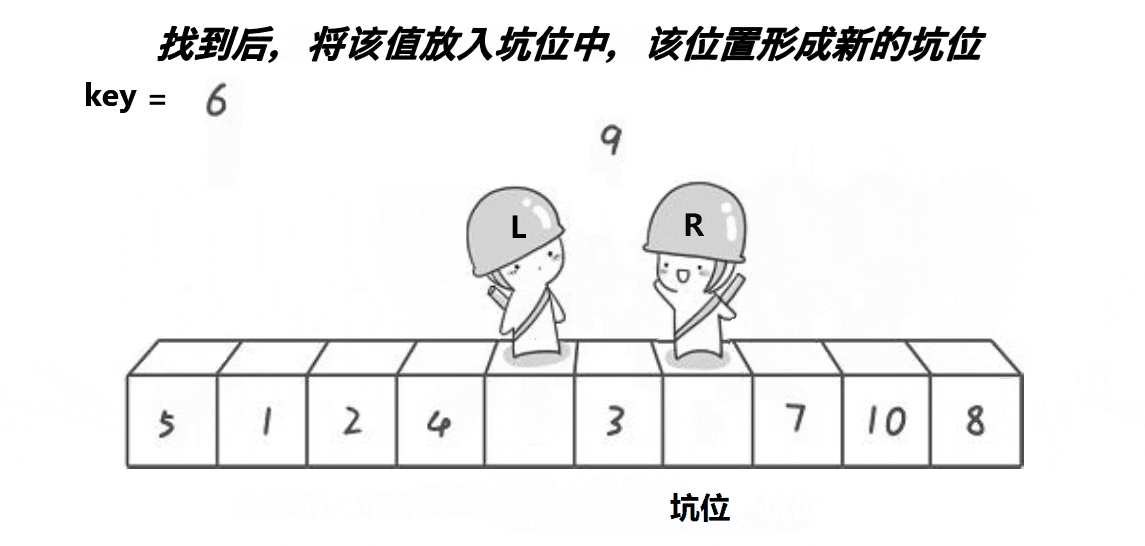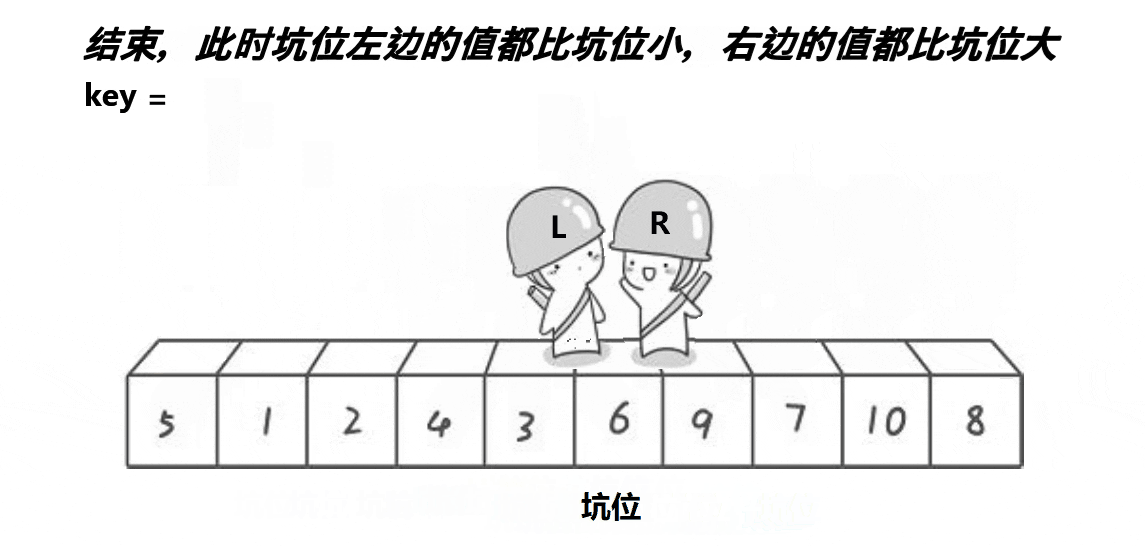
ⅱ挖坑法版本（单趟）

代码实现如下：


//快排单趟排序（挖坑法）
int qsort2(int* a, int left, int right) {
	std::cout << "left : " << left << " right : " << right << std::endl;
	int begin = left;
	int end = right;
	int keyi = begin;
	int tem = a[keyi];
	while (begin < end) {
		while (begin < end && a[end] >= tem) {
			end--;
		}		
		if (begin < end) {
			a[keyi] = a[end];
			keyi = end;
		}
		while (begin < end && a[begin] < tem) {
			begin++;
		}
		if (begin < end) {
			a[keyi] = a[begin];
			keyi = begin;
		}
	}
	a[begin] = tem;
	return keyi;
}

ⅲ前后指针法（单趟）

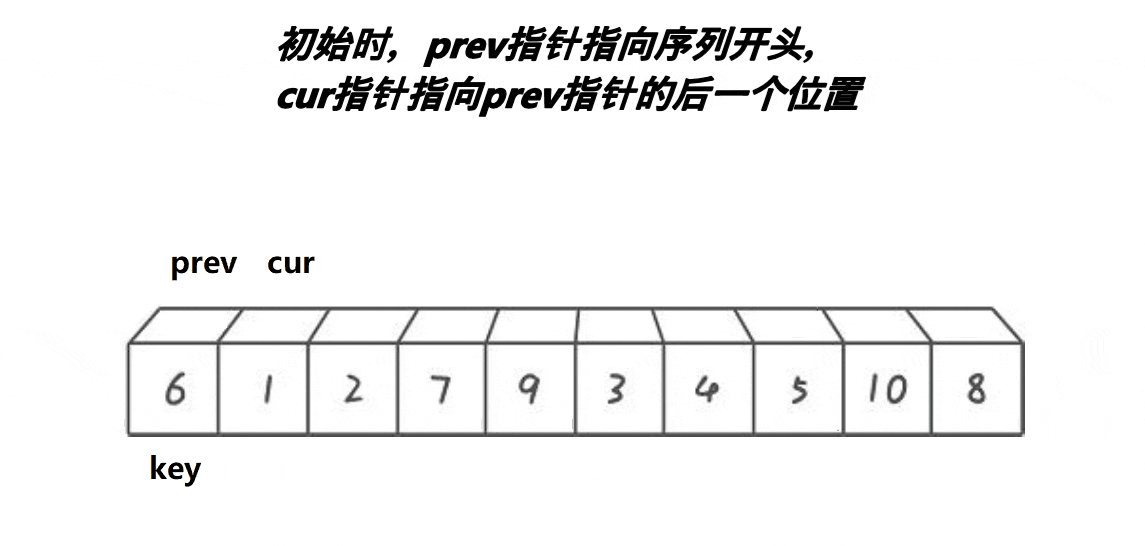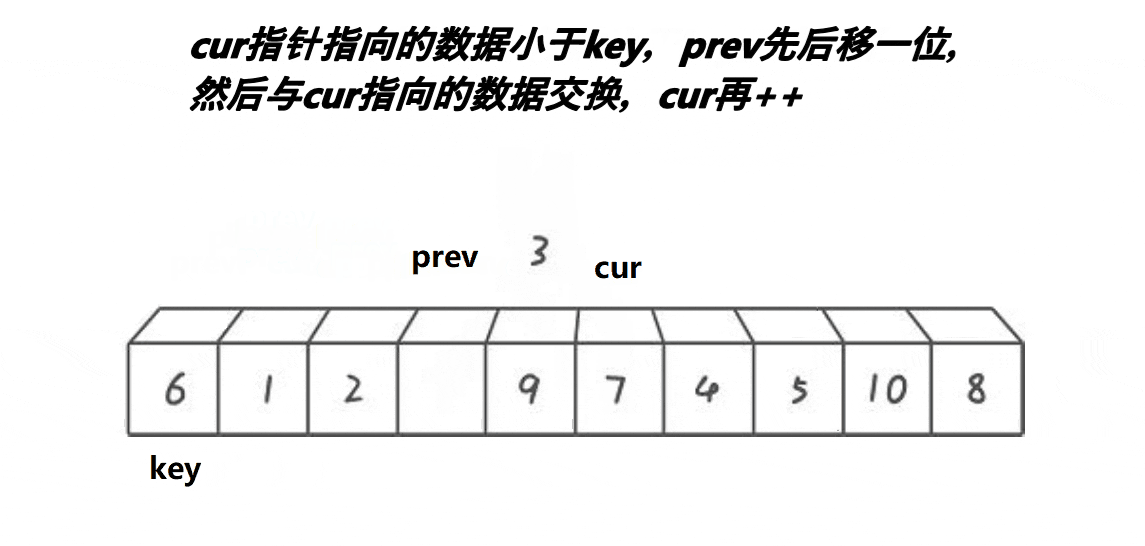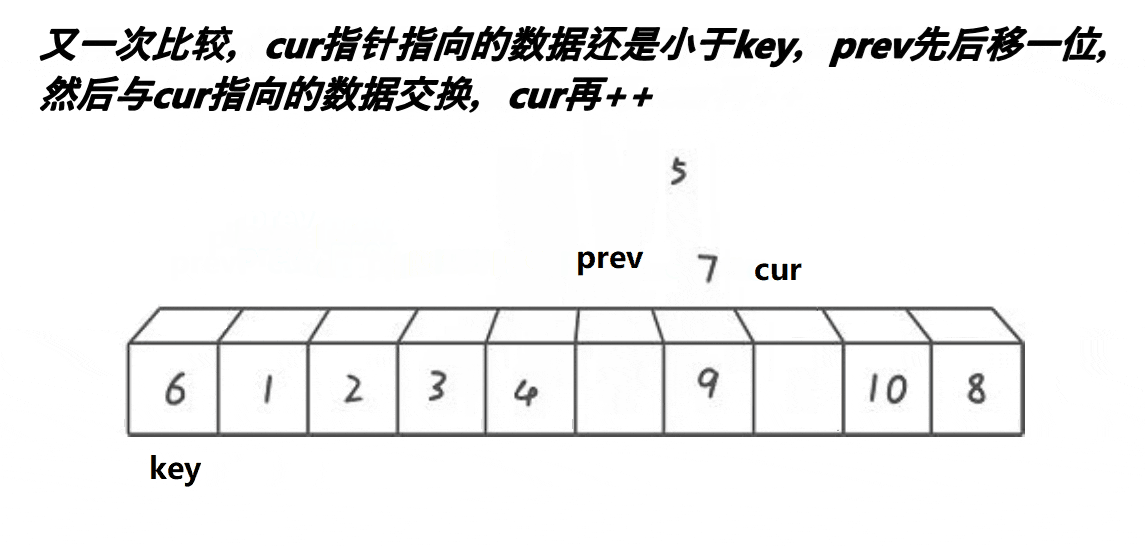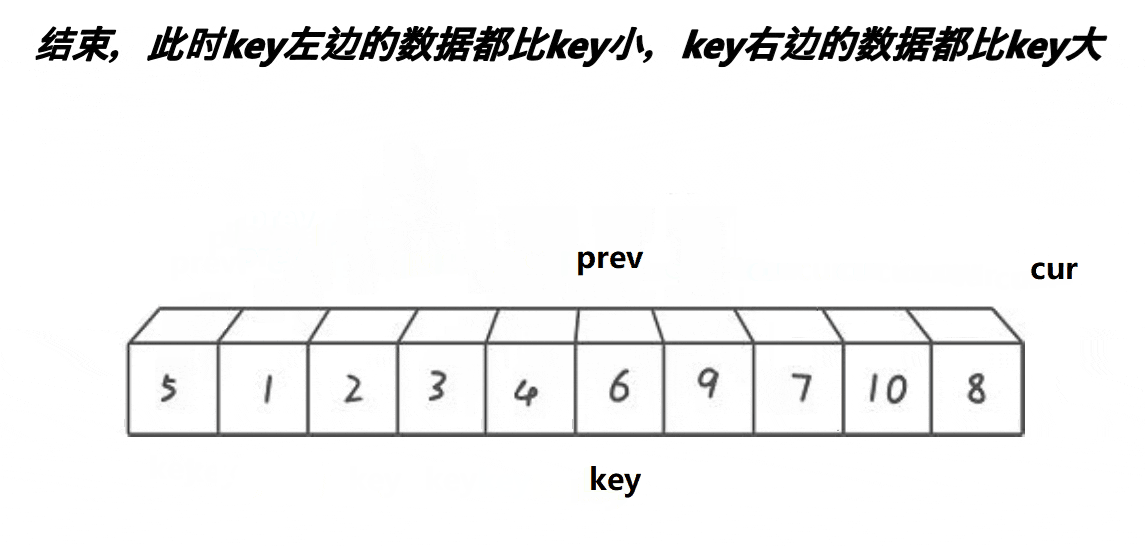
代码实现如下：

//快排单趟排序（前后指针法）
int qsort3(int* a, int left, int right) {
    int cur = left;
    int prev = cur;
    int keyi = left;
    while (cur <= right) {
        if (a[cur] <a[keyi]&&prev++!=cur) {
            Swap(&a[prev], &a[cur]);
        }
        cur++;
    }
    Swap(&a[keyi], &a[prev]);
    keyi = prev;
    return keyi;
}

②快排递归实现

//快排
void quickSort(int* a, int left,int right) {
	if (left >= right) {
		return;
	}
	int keyi=qsort1(a, left, right);
	quickSort(a, left, keyi - 1);
	quickSort(a, keyi + 1, right);

}

③快排非递归

使用栈或者队列来实现与递归相同的效果，可以看到，如果key取的位置接近二分的位置时，递归的过程就相当于二叉树中的前序遍历，我们将讲述用栈来模拟与前序遍历类似的效果。

代码实现如下：

//快排非递归
void QuickSort2(int* a, int left, int right) {
	int begin = left;
	int end = right;
	ST st;
	STInit(&st);
	STPush(&st, end);
	STPush(&st, begin);
	while (!isEmpty(&st)) {
		begin = STTop(&st);
		STPop(&st);
		end = STTop(&st);
		STPop(&st);
		int keyi = qsort2(a, begin, end);
		if (keyi + 1 < end) {
			STPush(&st, end);
			STPush(&st, keyi + 1);
		}
		if (begin < keyi - 1) {
			STPush(&st, keyi - 1);
			STPush(&st, begin);
		}
	}
	STDestroy(&st);    
	

}

这里采用的单趟排序是挖坑法，篇幅有限，栈的实现并没有给出。

④快排优化

我们可以对快排进行一些优化来提高快排的效率

ⅰ三数取中

我们都知道当key将序列进行二分时，栈的深度接近logN,但是在序列为有序排列选择left当成key时会使得栈的深度接近N，当数据量很大的时候会有爆栈的风险。

这时我们进行三数取中改变key值，就是为了避免这种有序情况的出现。因为选key固定key的位值，我们只需要找到中间的那个数进行固定区间递归的高度将会变为 $\log n$ 从而解决了爆栈的风险。

这里以hoare单趟排序为例，代码如下:

//快排单趟排序(霍尔)
int qsort1(int* a, int left, int right) {
	int begin = left;
	int end = right;
	//三数取中优化
	int mid = Getmid(a, left, right);
	Swap(&a[begin], &a[mid]);
	int keyi = begin;
	//右边找小，左边找大
	
		while (begin < end) {
			while (begin < end && a[end] >= a[keyi]) {
				end--;
			}
			while (begin < end && a[begin] <= a[keyi]) {
				begin++;
			}

			Swap(&a[begin], &a[end]);
		}
		Swap(&a[begin], &a[keyi]);
		return begin;
	}

ⅱ小区间优化

当区间被划分的很小时，这时用快排单趟排序来开辟栈帧效率并不高，这是我们会选择其他排序算法。这里以直接插入排序来代替，当区间小于10时，采用插入排序进行。

void quickSort(int* a, int left,int right) {
	if (left >= right) {
		return;
	}
	if (right - left + 1 < 10) {
		InsertSort(a, right - left + 1);
		return;
		//当快排到最后的排序数量小于一定值的时候可以考虑插入排序
	}
	int keyi=qsort1(a, left, right);
	quickSort(a, left, keyi - 1);
	quickSort(a, keyi + 1, right);

}

四.归并排序

时间复杂度 O（N^logN）

归并排序的思想就是分治法(分而治之)，将序列分成若干区间进行排序之后在合并，归并的实现有两种递归与非递归，接下来我将进行讲述：

i 归并递归实现

代码如下：

//归并
//归并的递归排法
void mergeSort(int* a,int *tem,int left,int right) {
	if (left >= right) {
		return;
	}
	int mid = (left + right) / 2;
	int begin1 = left;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = right;
	int j = begin1;
	mergeSort(a, tem,begin1, end1);
	mergeSort(a,tem, begin2, end2);//左边归并排好序右边归并排好序，直接合并来
	
	while (begin1 <=end1 && begin2 <=end2) {
		if (a[begin1] < a[begin2])
			tem[j++] = a[begin1++];
		else
			tem[j++] = a[begin2++];
	
	}
	while (begin1 <= end1) {
		tem[j++] = a[begin1++];
	}
	while (begin2 <= end2) {
		tem[j++] = a[begin2++];
	}
	memcpy(a+left, tem+left, sizeof(int)*(right-left + 1));

	
}

ii 归并的非递归版本

代码如下：

//非递归版本的归并
void MergeSortNonR(int* a, int n) {
	int* tem = (int*)malloc(sizeof(int) * n);
	mergeSort2(a, tem, n);

}
void mergeSort2(int* a, int* tem, int n) {

	int gap = 1;
	while (gap <n) {
		for (int i = 0; i < n; i += 2*gap) {
			int begin1 = i;
			int end1 = i + gap - 1;//要考虑其他值大于n的情况
			int begin2 = i + gap;
			int end2= i + 2 * gap - 1;//接着要进行排序；

			int j = begin1;
			if (begin2 >= n) 
				break;
			
			if (end2 >= n ) 
				end2 = n-1;
			

			while (begin1 <= end1 && begin2 <= end2) {
				if (a[begin1] < a[begin2])
					tem[j++] = a[begin1++];
				else
					tem[j++] = a[begin2++];

			}
			while (begin1 <= end1) {
				tem[j++] = a[begin1++];
			}
			while (begin2 <= end2) {
				tem[j++] = a[begin2++];
			}
			memcpy(a + i, tem + i, sizeof(int) * (end2-i+1));
		}

		gap *= 2;

	}




}

五.拓展

非比较排序(计数排序)

时间复杂度 O（N+range），空间复杂度 O（range）

计数排序不需要进行比较排序，是一种牺牲空间换取时间的做法，当range>>n时，其效率反而不如基于比较的排序算法，其代码实现如下：

//计数
void coutSort(int* a, int n) {
	int max, min;
	max = min = a[0];
	for (int i = 1; i < n; i++) {
		if (a[i] >max) {
			max = a[i];
		}
		if (a[i] < min) {
			min = a[i];
		}
	}
	int range = max - min + 1;
	int* count = (int*)calloc(range,sizeof(int) );
	for (int i = 0; i <n; i++) {
		count[a[i] - min]++;
	}
	int m = 0;
	for (int j = 0; j < range;j++) {
		while (count[j]) {
			a[m++] = j + min;
			count[j]--;
		}
	}

}

排序算法总结到此。