DATAWHALE-李宏毅机器学习-3

回归误差

Errors与Bias

• 假设$\hat{f}$是最佳的model(function)，我们从training data中所找出的$f^{\ast }$实际上是$\hat{f}$的估测值(estimator)。$f^{\ast }$与$\hat{f}$间的差距可以类比与靶心和落靶位置之间的距离。这个差距来源于Bias(瞄准的位置和$\hat{f}$间的差距)和Variance(落点和瞄准的位置)。
  (from李宏毅老师课程中的slides）
  
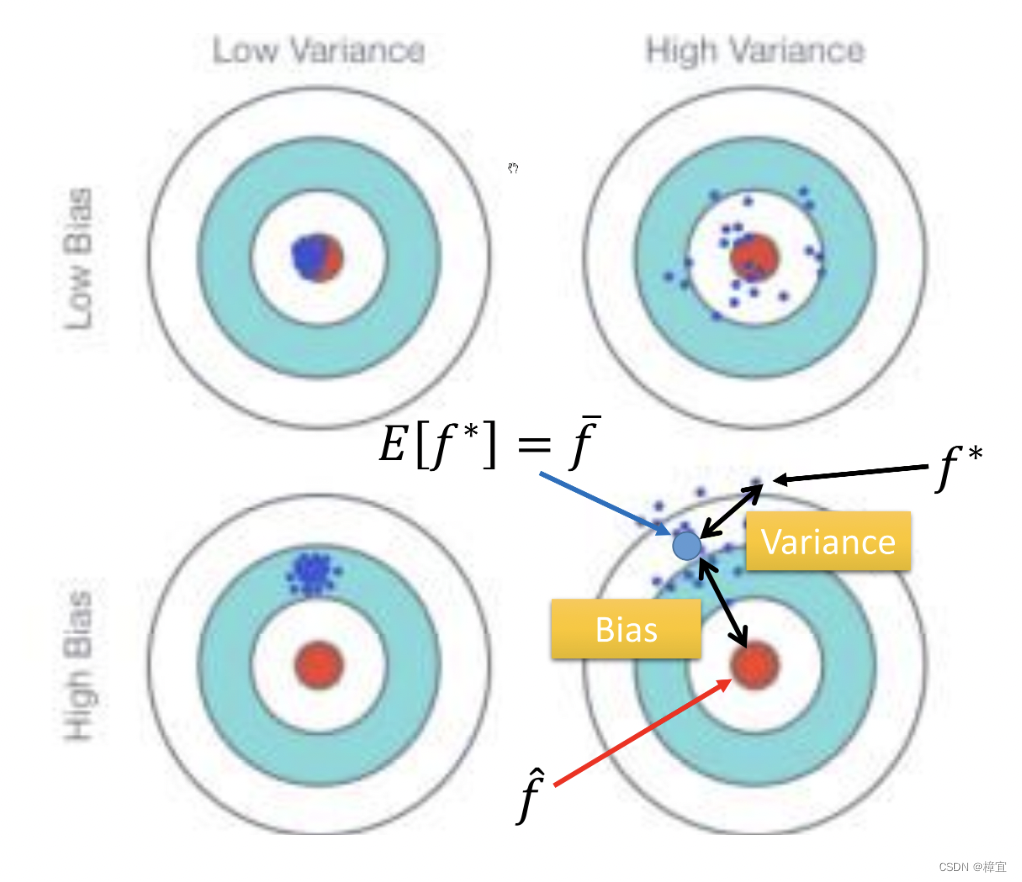
• 复杂的模型：small bias and large variance overfitting
• 简单的模型：large bias and small variance under fitting
• 想要improve model的时候要诊断是 bias还是variance大。对于bias来说，redesign your model，比如添加更多的features或者改变次幂项做更复杂的模型。对于large variance，更多的data(一般不具有实际性，但是或许可以根据经验或者知识自己造数据)或者正则化(Regularization)
• 在bias和variance之间做出trade-off。
  Training set选择出的error最小的model，在Testing set上的效果不一定是最好的。

Gradient Descent

梯度下降法的核心是寻找参数使得L(Loss function)到最小值。
${\theta }^{\ast }=\arg \underset{\theta }{\min }L(\theta )$ 其中$\theta$是一族参数(parameters)。
对$\theta$进行迭代计算。如下：
$$\nabla L(\theta )=\left[\begin{array}{c}\frac{\partial L({\theta }_1)}{\partial L({\theta }_1}\\ \frac{\partial L({\theta }_2)}{\partial L({\theta }_2}\end{array}\right]$$
迭代式：
$${\theta }^1={\theta }^0-\eta \nabla L({\theta }^0)$$
$\eta$被称为学习率(Learning rate)

调整学习率至关重要

• 一些相关算法的出现的出现
  简单的思想，例如随着次数的增加，通过一些因子来减少学习率，学习率依照不同情形情况设置，没有通用的值
• Adagrad 算法 (每个参数的学习率都除以之前微分的均方根)
  $$w^{t+1}\leftarrow w^t-\frac{\eta }{{\sum }_{i=0}^t(g^i{)}^2}{g}^t$$
  单参数函数（想一下二次函数求极值的例子）中，梯度越大，就跟最低点的距离越远。但是在多参数下，这个结论不一定成立。与最低点间的距离（即梯度下降移动的步伐）不止和一次微分成正比，还和二次微分成反比。于是应：$\frac{｜一次微分｜}{二次微分}$使用${\sum }_{i=0}^t(g^i{)}^2$来近似二次微分（省时省力）。
• 随机梯度下降法（Stochastic Gradient Descent）
  喂一组数据就更新一次梯度，不需要像梯度下降法每次更新梯度使用所有的数据。
  -特征缩放（make different features have the same scaling）
  使多个参数在更新梯度时学习率尽量一致。
  $${x_i^r}^{\prime }\leftarrow \frac{x_i^r-m_i}{{\sigma }_i}$$ 使每一组特征的平均值为0，方差为1（标准化）。

梯度下降的数学理论

每次更新参数，不一定使得损失函数更小。
泰勒展开的前提即h(x)在$x=x_0$点的某个领域内有无限阶导数(即无限可微分，infinite differentiable)，在$x_0$的邻域内有
$$\begin{array}{rl}h(x)& =\sum _{k=0}^{\infty }\frac{h(x_0^k)}{k!}(x-x_0{)}^k\\ & =h(x_0)+h^{\prime }(x_0)(x-x_0)+\frac{h^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2\end{array}$$
当$x$接近$x_0$时，有$$h(x)\approx h(x_0)+h^{\prime }(x_0)(x-x_0)$

梯度下降的限制

• 容易陷入局部极值
• 微分是0，但不是极值
• 还有可能微分值趋近于0或者小于某一个数（例如$10^{-6}$）比较平缓，但并不是极值点