神经网络：全连接神经网络（单层结构）

本文链接：https://blog.youkuaiyun.com/rusi__/article/details/104216514

介绍

首先，要先了解一下逻辑回归。
在逻辑回归中，其实是通过sigmoid函数将线性回归输出值转换成0~1之间的概率值，从而通过阈值（常为0.5）比较实现二分类问题求解。
而在神经网络解决多分类问题时，便是通过softmax函数，将每个样本的输出值转换为一个概率值，比较概率值的大小，实现多分类问题的求解。
softmax函数：
- 公式：
- 公式介绍：我们假设存在一组数据：样本为三个特征的三分类问题。那么一个样本的在神经网络的计算过程会呈现下图状态。
  
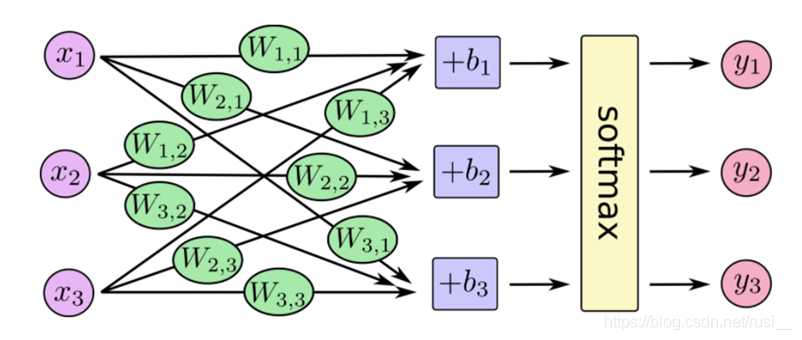
  1、第一步，我们假设全连接层的神经元输出为40,50,60。
  2、第二步，那么softmax函数的计算规则为：y1 = e ^40 /(e ^40+e ^50+e ^60)。
损失函数：交叉熵损失函数。
- 公式：
- 公式参数介绍：1、𝑦𝑖 为真实结果的概率值（此处为1）,𝑦𝑖’ 为神经网络预测结果的概率值，。2、每个样本都有一个损失值，所以最后需要求平均损失为衡量标准。
- 公式详细介绍：
  1、需要提前知道的是，在神经网络多分类问题中，目标值必须为ont-hot编码（这是为了方便损失函数计算）。
  2、对于对数函数特性而言（此时a=2>1），yi的值越大 - log(yi)的值越小。
  3、我们假设存在一组数据：样本为三个特征的三分类问题。假设其中某一个样本的在某一次优化权重的时候，预测结果的概率为：[0.2,0.3,0.5]，对应着的预测值为[0,0,1]，而真实值为[1,0,0]。则此时该样本损失值为：Hy’(y) = - ( 1log(0.2) + 0log(0.3) +0log(0.5)) = - log(0.2)。
  4、关于上面一个计算做个小总结：由于该次预测值偏离真实值，所以损失函数的损失值必然大，根据对数函数特性，-log(0.2)>-log(0.5)，符合损失函数特性。
  5、假设预测的结果完全正确，概率体现为：[1,0,0]，对应着预测值为[1,0,0]，而真实值为[1,0,0]，此时该样本的损失值为 Hy’(y) = - 1log(1)+0+0 = 0。
优化函数：交叉熵损失函数反向传播算法求解（其实就是梯度下降~~）。
- 命名为反向传播的原因是：在神经网络中隐层可能存在多层神经元（感知机- - -其实就是一个函数），类似一个正向传播的过程，那么通过梯度下降就要反向的更新权重，找寻最优解。

案例

需求：手写数字识别
数据集：tensorflow自带数据集（下载四个.gz并解压）
流程：1、准备数据；2、数据占位符；3、建立模型，随机初始化权重和偏置；4、计算平均损失值；5、梯度下降优化。

code：

#!/usr/local/bin/python3
# -*- coding: utf-8 -*-
# Author  : rusi_
import os

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
from tensorflow.contrib.slim.python.slim.nets.inception_v3 import inception_v3_base

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'


def minst_test():
    """
    单层网络，手写数字预测
    :return:
    """
    # 获取数据
    mnist = input_data.read_data_sets(r"E:\mac_obj_file\mnist", one_hot=True)
    # 建立数据占位符
    with tf.variable_scope("data"):
        x = tf.placeholder(tf.float32, [None, 784])
        y_true = tf.placeholder(tf.float32, [None, 10])
    # 建立一个简单的全连接层神经网络模型
    with tf.variable_scope("model"):
        w = tf.Variable(tf.random_normal([784, 10], mean=0, stddev=1.0), name="w")
        b = tf.Variable(tf.constant(0.0, shape=[10]))
        y_predict = tf.matmul(x, w) + b
    # 损失函数
    with tf.variable_scope("loss"):
        loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_true, logits=y_predict))
    # 优化：梯度下降
    with tf.variable_scope("optimizer"):
        train_op = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
    # 计算准确率
    with tf.variable_scope("accuracy"):
        # one-hot
        equal_list = tf.equal(tf.argmax(y_true, 1), tf.argmax(y_predict, 1))
        accuracy = tf.reduce_mean(tf.cast(equal_list, tf.float32))

    # 事件可视化
    # 收集变量
    tf.summary.scalar("losses", loss)
    tf.summary.scalar("acc", accuracy)
    tf.summary.histogram("weightes", w)
    tf.summary.histogram("biases", b)
    # 合并变量的op
    merged = tf.summary.merge_all()
    
    # 保存模型的实例
    saver = tf.train.Saver()
    
    # 定义一个初始化变量的op
    init_op = tf.global_variables_initializer()
    
    # run
    with tf.Session() as sess:
        sess.run(init_op)
        
        # 写手
        file_writer = tf.summary.FileWriter("./obj_file/minst_test/", graph=sess.graph)
        
        # 打开保存了的模型
        if os.path.exists("./ckpt/minst_test/checkpoint"):
            saver.restore(sess, "./ckpt/minst_test/model")

        for i in range(2000):
            mnist_x, mnist_y = mnist.train.next_batch(50)
            sess.run(train_op, feed_dict={x: mnist_x, y_true: mnist_y})
            # 写入
            summary_ = sess.run(merged, feed_dict={x: mnist_x, y_true: mnist_y})
            file_writer.add_summary(summary_, i)
            
            print(f"训练第：{i}步，准确率：{sess.run(accuracy, feed_dict={x: mnist_x, y_true: mnist_y})}")
            
        # 保存模型
        saver.save(sess, "./ckpt/minst_test/model")


if __name__ == '__main__':
    minst_test()

# tensorboard --logdir="./obj_file/minst_test/" 查看优化状况

补充：

从抽象的角度上讲，其实神经网络是由多个线性回归组成，而每个线性回归就是一个感知机。如果拿全连接层做例来看：
- 线性回归（单个感知机）：如果要处理分类问题，那么输出（sum）会由sigmoid函数处理得到一个概率，概率大小与阈值（多为0.5）比较从而处理二分类问题。
- 神经网络（多个感知机）：如果要处理分类问题，输出（sum）会由softmax函数处理得到多个概率，概率最大的为真实的预测的目标值，从而处理多分类问题。