【算法集训专题攻克篇】第二十五篇之树状数组

最新推荐文章于 2025-12-19 15:31:04 发布

原创最新推荐文章于 2025-12-19 15:31:04 发布 · 188 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #深度优先 #leetcode

算法集训专栏收录该内容

57 篇文章

订阅专栏

本文介绍了如何利用树状数组解决LeetCode题目327——区间和的个数问题，涉及离散化前缀和、更新查询操作。通过实例演示了算法的魅力，引导读者提升算法能力。

《算法集训传送门》

👉引言

在这里插入图片描述

	铭记于心
	🎉✨🎉我唯一知道的，便是我一无所知🎉✨🎉

💖 ❄️我们的算法之路❄️💖

众所周知，作为一名合格的程序员，算法能力是不可获缺的，并且在算法学习的过程中我们总是能感受到算法的✨魅力✨。
☀️🌟短短几行代码，凝聚无数前人智慧；一个普通循环，即是解题之眼🌟☀️
💝二分，💝贪心，💝并查集，💝二叉树，💝图论，💝深度优先搜索(dfs)，💝宽度优先搜索（bfs），💝数论，💝动态规划等等， 路漫漫其修远兮，吾将上下而求索！希望在此集训中与大家共同进步，有所收获！！！🎉🎉🎉

今日主题：树状数组

👉⭐️第一题💎

✨题目

327. 区间和的个数 - 力扣（LeetCode）

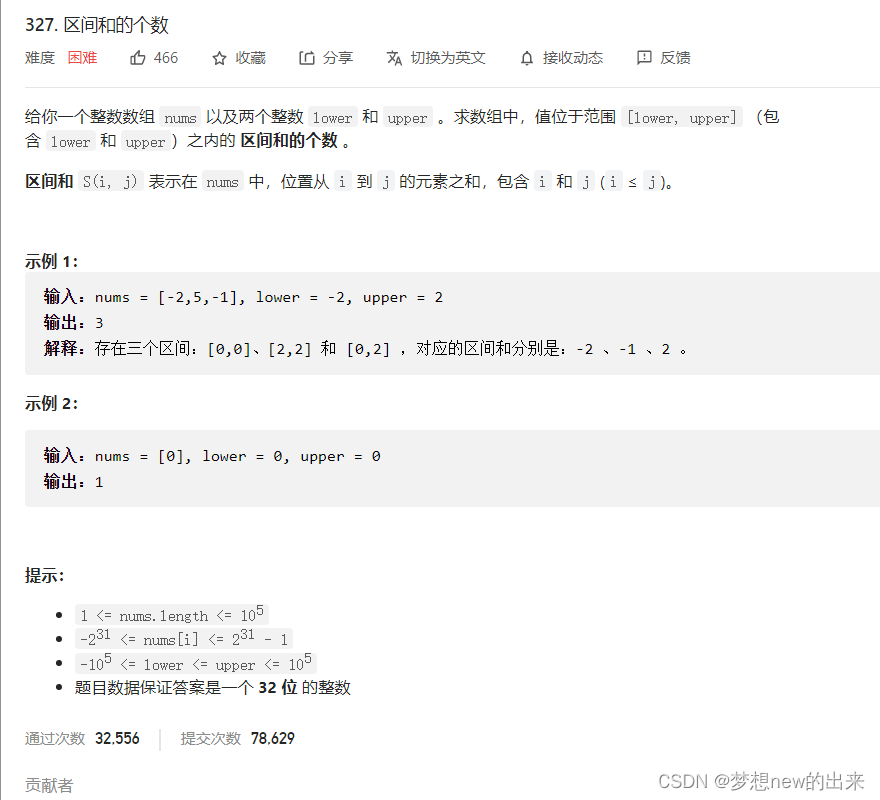
在这里插入图片描述

1、离散化前缀和
2、更新查询前缀和

✨代码：

class Solution:

    def countRangeSum(self, nums: List[int], lower: int, upper: int) -> int:
        if not nums:
            return 0
        # 离散化
        sums = [0]
        for num in nums:
            sums.append(sums[-1] + num)
        vals = set()
        for num in sums:
            vals |= {num, num + lower, num + upper}
        vals = sorted(vals)
        index = {}
        for i, num in enumerate(vals):
            index[num] = i
        n = len(vals)
        c = [0] * n

        # 定义树状数组函数
        def lowbit(x):
            return x & -x

        def update(i):
            i += 1
            while i <= n:
                c[i - 1] += 1
                i += lowbit(i)

        def getsum(i):
            res = 0
            i += 1
            while i >= 1:
                res += c[i - 1]
                i -= lowbit(i)
            return res

        # 更新查询树
        ans = 0
        for num in sums[::-1]:
            left, right = index[num + lower], index[num + upper]
            ans += getsum(right)
            if left > 0:
                ans -= getsum(left - 1)
            update(index[num])
        return ans
。