寻找数组的中心索引
给定一个整数类型的数组 nums,请编写一个能够返回数组“中心索引”的方法。
我们是这样定义数组中心索引的:数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。
如果数组不存在中心索引,那么我们应该返回 -1。如果数组有多个中心索引,那么我们应该返回最靠近左边的那一个。
//c++
class Solution {
public:
int pivotIndex(vector<int>& nums) {
auto begin = nums.begin();
auto end = nums.end();
int cnt = 0;
int subsum = 0;
int sum = 0;
if (begin != end)
{
//第一次遍历先求和
for (auto p = begin; p != end; p++)
{
sum = *p + sum;
}
//第二次遍历找中心索引(通过索引两边的和一样来判断)
for (auto p = begin; p != end; p++)
{
subsum = *p + subsum;
cnt++;
if ((sum - subsum + *p)==subsum)
{
return cnt-1;
}
}
return -1;
}
else
return -1;
}
};
至少是其他数字两倍的最大数
在一个给定的数组nums中,总是存在一个最大元素 。
查找数组中的最大元素是否至少是数组中每个其他数字的两倍。
如果是,则返回最大元素的索引,否则返回-1。
class Solution {
public:
int dominantIndex(vector<int>& nums) {
int index_max = -1;
int flag = 0;
int max = 0;
//先找最大值和最值对应的索引
for (auto i = 0; i < nums.size(); i++)
{
if (nums[i] > max)
{
max = nums[i];
index_max = i;
}
}
//遍历数组
for (auto i = 0; i < nums.size() ; i++)
{
if (i == index_max)
{
continue;
}
if (2 * nums[i] > max)
{
flag = 1;
}
}
if (flag == 1)
{
return -1;
}
else
{
return index_max;
}
}
};
加一
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储一个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
class Solution {
public:
vector<int> plusOne(vector<int>& digits) {
auto begin = digits.begin();
auto end = digits.end();
int flag=0; //进位标记
*(end - 1)=*(end - 1)+1; //最后一位+1
for (auto p = end-1; p != begin; p--)
{
if (flag==0 && *p == 10)
{
*p = 0;
flag = 1;
}
else if(flag==1)
{
(*p)++;
if (*p == 10)
{
*p = 0;
flag = 1;
}
else
{
flag = 0;
}
}
}
if (flag == 1)
{
*begin = *begin + 1;
}
//遍历到最后,如果第一位是10的情况下,使其变为[1,0]
if (*begin == 10)
{
*begin = 0;
digits.insert(begin, 1);
}
return digits;
}
};
对角线遍历
给定一个含有 M x N 个元素的矩阵(M 行,N 列),请以对角线遍历的顺序返回这个矩阵中的所有元素,对角线遍历如下图所示。

解题关键在于:
1.每一趟的坐标(x,y),x+y总是相等的,且随着每一趟加1
2.每一趟的x,y的取值范围需要考虑,不能超过矩阵的边界
class Solution {
public:
vector<int> findDiagonalOrder(vector<vector<int>>& matrix) {
vector<int> result;
//空容器直接返回结果
if(matrix.size() == 0)
{
return result;
}
if((matrix[0].size()==0))
{
return result;
}
int row = matrix.size()-1;
int column = (*(matrix.begin())).size()-1;
int i = 0, j = 0;
int sum = row + column;
int temp = 0;//循环每一趟的条件
int flag = 0;//作为每一趟正反向的标致,和边界条件
while (temp <= sum)
{
if (flag % 2 == 0) //正向
{
i = flag; //边界条件的设置
if (i > row) //正向,i都在递减,j都在递增
{
i = row;
}
j = temp - i;
if (j<0)
{
j = 0;
}
while (i >= 0 && j <= column)
{
result.push_back(matrix[i][j]);
i--;
j++;
}
flag++;
}
else if (flag % 2 == 1) //反向
{
j = flag;
if (j > column)
{
j = column;
}
i = temp-j;
if (i< 0)
{
i = 0;
}
while (i <= row && j >= 0)
{
result.push_back(matrix[i][j]);
i++;
j--;
}
flag++;
}
temp++;
}
return result;
}
};
螺旋矩阵
给定一个包含 m x n 个元素的矩阵(m 行, n 列),请按照顺时针螺旋顺序,返回矩阵中的所有元素。
解题思路:按层遍历(分上,右,下,左依次)

class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> result;
if(matrix.size()==0)
{
return result;
}
if(matrix[0].size()==0)
{
return result;
}
int row = matrix.size(); //行
int column = matrix[0].size(); //列
//右下角坐标必定是(row-1,column-1)
row = row - 1;
column = column - 1;
//左上角坐标必定是(0,0)
int i = 0, j = 0; //左上角初始坐标
int x = 0, y = 0; //遍历时的坐标
while (i < row && j < column)
{
//top
for (y=j;y <= column; y++)
{
result.push_back(matrix[i][y]);
}
//right
for (x=i+1; x <= row; x++)
{
result.push_back(matrix[x][column]);
}
//bottom
for (y = column-1; y > j; y--)
{
result.push_back(matrix[row][y]);
}
//left
for (x = row; x > i; x--)
{
result.push_back(matrix[x][j]);
}
//进入里一层
i++;
j++;
row--;
column--;
}
//针对[[2],[3]]等类似的情况
if ((i <= row && j <= column))
{
for (x = i; x <= row; x++)
{
for (y = j; y <= column; y++)
{
result.push_back(matrix[x][y]);
}
}
}
return result;
}
};
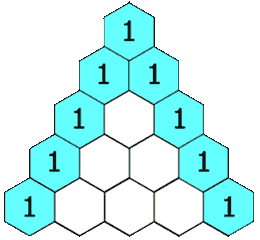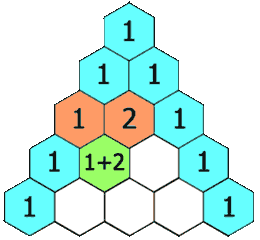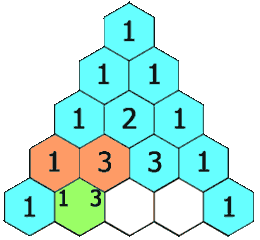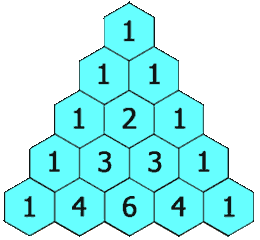
杨辉三角
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> generate;
if(numRows==0)
{
return generate;
}
else
{
for (int i = 1; i <= numRows; i++)
{
vector<int> temp;
if (i == 1)
{
temp.push_back(1);
generate.push_back(temp);
}
else if(i == 2)
{
temp.push_back(1);
temp.push_back(1);
generate.push_back(temp);
}
else //从第三层开始6
{
temp.push_back(1);
temp.push_back(1);
for (int x = 0; x < i - 2; x++) //每一层等于上一层的2值之和
{
auto p = temp.begin();
int sum = generate[i - 2][x] + generate[i - 2][x + 1];
temp.insert(p+1, sum);
}
generate.push_back(temp);
}
}
}
return generate;
}
};
二进制求和
给定两个二进制字符串,返回他们的和(用二进制表示)。
输入为非空字符串且只包含数字 1 和 0。
class Solution {
public:
string addBinary(string a, string b) {
string result;
int flag = 0; //初始进位标志为0
//交换a,b,保证a的长度大于等于b
if (a.length() < b.length())
{
result = a;
a = b;
b = result;
}
//结果保存在多出一位的字符串中,并默认所有字符串位为0
result.resize(a.length() + 1, '0');
//将b的前几位补0
int length = a.length() - b.length();
if(a.length()>b.length())
{
for (int i = 0; i <length; i++)
{
auto p = b.begin();
b.insert(p, '0');
}
}
//执行两数相加
for (int i = a.length() - 1; i >= 0; i--)
{
if (a[i] == '0' && b[i] == '0')
{
if (flag == 0)
{
result[i + 1] = '0';
flag = 0;
}
else if (flag == 1)
{
result[i + 1] = '1';
flag = 0;
}
}
else if ((a[i] == '0' && b[i] == '1') || (a[i] == '1' && b[i] == '0'))
{
if (flag == 0)
{
result[i + 1] = '1';
flag = 0;
}
else if(flag == 1)
{
result[i + 1] = '0';
flag = 1;
}
}
else if (a[i] == '1' && b[i] == '1')
{
if (flag == 0)
{
result[i + 1] = '0';
flag = 1;
}
else if(flag == 1)
{
result[i + 1] = '1';
flag = 1;
}
}
}
//最后如果进位标志为1则置1,为0则删除首位
if (flag == 1)
{
result[0] = '1';
}
else
{
result.erase(0, 1);
}
return result;
}
};
最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 “”。
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
string result={};
if(strs.size()==0)
{
return result;
}
int nums = strs.size();
int minlen = 0;
int flag = -1; //标志位记字符串的异同//同时也用来记字符串存在不同时的位置
//得到最短的字符串长度
minlen = strs[0].size();
for (int i = 0; i < nums; i++)
{
if (strs[i].size() <= minlen)
{
minlen = strs[i].size();
}
}
//查找最长公共前缀
for (int i = 0; i < minlen; i++)
{
if (flag == -1)
{
for (int j = 0; j < nums - 1; j++)
{
if (strs[j][i] == strs[j + 1][i])
{
flag = -1;
}
else
{
flag = i;
break;
}
}
}
else
{
break;
}
}
if (flag == 0) //字符串第一个位置便存在差异,所以直接返回
{
return result;
}
else if (flag == -1) //字符串按照最短长度遍历完,则最长公共前缀就是最短的那个字符串
{
result.append(strs[0], 0, minlen);
return result;
}
else //其他情况根据不同的字符串位置
{
cout << flag << endl;
result.append(strs[0], 0, flag);
return result;
}
}
};
反转字符串
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
class Solution {
public:
void reverseString(vector<char>& s) {
if(s.size()==0)
{
s={};
}
else
{
char temp;
for (auto begin = s.begin(),end = s.end() - 1; begin <= end; begin++, end--)
{
temp = *begin;
*begin = *end;
*end = temp;
}
}
}
};
两数之和 II - 输入有序数组
给定一个已按照升序排列 的有序数组,找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2,其中 index1 必须小于 index2。
说明:
返回的下标值(index1 和 index2)不是从零开始的。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
vector<int> twoSum;
int len = numbers.size(); //有序数组的长度
for (int i = 0; i <= len - 1; i++)
{
for (int j = i + 1; j <= len - 1; j++)
{
if (target - numbers[i] == numbers[j])
{
twoSum.push_back(i + 1);
twoSum.push_back(j + 1);
}
//考虑到[0,0,0,.....9,9,9,9,9]等输入情况,设置一个跳出循环
if (numbers[i] == numbers[i + 1])
{
break;
}
}
}
return twoSum;
}
};
官方解答有更优质的思路
我们使用两个指针,初始分别位于第一个元素和最后一个元素位置,比较这两个元素之和与目标值的大小。如果和等于目标值,我们发现了这个唯一解。如果比目标值小,我们将较小元素指针增加一。如果比目标值大,我们将较大指针减小一。移动指针后重复上述比较知道找到答案。
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int low = 0, high = numbers.size() - 1;
while (low < high) {
int sum = numbers[low] + numbers[high];
if (sum == target)
return {low + 1, high + 1};
else if (sum < target)
++low;
else
--high;
}
return {-1, -1};
}
};
//作者:LeetCode
移除元素
给定一个数组 nums 和一个值 val,你需要原地移除所有数值等于 val 的元素,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
解题的方式在于快慢指针
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int k = 0; //k为慢指针
if(nums.size()==0)
{
return k;
}
int len = nums.size()-1;
for (int i = 0; i <=len ; i++) //i为快指针
{
if (nums[i] != val)
{
nums[k] = nums[i];
k++;
}
}
return k;
}
};
最大连续1的个数
给定一个二进制数组, 计算其中最大连续1的个数。
class Solution {
public:
int findMaxConsecutiveOnes(vector<int>& nums) {
int maxn=0;
int n=0;
for(int i=0;i<nums.size();i++)
{
if(nums[i]){
n++;
maxn=max(n,maxn);
}
else n=0;
}
return maxn;
}
};
长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组,返回 0。
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
if(nums.size()==0)
{
return 0;
}
int len = nums.size()-1;
int n = 0, sum = 0, minn =99999;
for (int i = 0; i <= len; i++)
{
sum = 0;
n = 0;
for (int j = i; j <= len; j++)
{
sum = sum + nums[j];
n++;
if (sum >= s)
{
minn = min(n, minn);
break;
}
}
}
if(minn==99999)
{
return 0;
}
else
{
return minn;
}
}
};
官方提供思路,使用双指针
我们用 2 个指针,一个指向数组开始的位置,一个指向数组最后的位置,并维护区间内的和 sum 大于等于 s 同时数组长度最小。
int minSubArrayLen(int s, vector<int>& nums)
{
int n = nums.size();
int ans = INT_MAX;
int left = 0;
int sum = 0;
for (int i = 0; i < n; i++) {
sum += nums[i];
while (sum >= s) {
ans = min(ans, i + 1 - left); //i+1-left 是当前子数组的长度
sum -= nums[left++]; //sum-nums[left]然后增加left //i是子数组结尾,left是子数组头
}
}
return (ans != INT_MAX) ? ans : 0;
}
//作者:LeetCode
旋转数组
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
1.解题思路 暴力
2.使用反转
class Solution {
public:
void rotate(vector<int>& nums, int k) {
int len=nums.size();
k=k%len;
auto start = nums.begin();
auto end = nums.end();
reverse(start, end); //第一次反转
auto start1 = nums.begin();
for (int i = 1; i <= k; i++)
{
start1++;
}
start = nums.begin();
reverse(start, start1); //前k个元素反转
start = nums.begin();
for (int i = 1; i <= k; i++)
{
start++;
}
end = nums.end(); //后面n-k个元素反转
reverse(start, end);
}
};
杨辉三角 II
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> getRow(rowIndex+1);
getRow[0] = 1;
for (int i = 1; i <= rowIndex; i++) //i代表行
{
for (int j = i; j >= 1; j--) //j是每一行的元素位置,从右向左求和赋值
getRow[j] = getRow[j]+getRow[j - 1];
}
return getRow;
}
};
翻转字符串里的单词
给定一个字符串,逐个翻转字符串中的每个单词。
·无空格字符构成一个单词。
·输入字符串可以在前面或者后面包含多余的空格,但是反转后的字符不能包括。
·如果两个单词间有多余的空格,将反转后单词间的空格减少到只含一个。
class Solution {
public:
string reverseWords(string s) {
string res;
int flag=0;
if(s.length()==0)
{
return s;
}
else if(s==" ")
{
return "";
}
vector<string::iterator> index; //用于存储每个单词的迭代器位置
auto start = s.begin();
auto end = s.end()-1;
//去除首尾空格
while(*start == ' ' && start!=end)
{
start++;
if (start == end && *start==' ')
{
return "";
break;
}
}
while (*end== ' ' && start != end)
{
end--;
}
s.assign(start, end+1);
//去除字符串中的多余空格
for (int i = 0; i <= s.length()-1; i++)
{
if (s[i] !=' ' && s[i+1]==' ')
{
res.push_back(s[i]);
res.push_back(' ');
}
else if (s[i] == ' ' && s[i + 1] == ' ')
{
continue;
}
else if(s[i] != ' ')
{
res.push_back(s[i]);
}
}
//反转字符串
reverse(res.begin(), res.end());
//单个字符串反转
for (auto p= res.begin();p< res.end();p++)
{
if (*p == ' ')
{
index.push_back(p);
}
}
if (index.size() == 0)
{
reverse(res.begin(), res.end());
}
else if (index.size() == 1)
{
reverse(res.begin(), index[0]);
reverse(index[0]+1, res.end());
}
else
{
reverse(res.begin(), index[0]);
for (int i = 0; i <= index.size()-2; i++)
{
reverse(index[i], index[i+1] + 1);
}
reverse(index[index.size()-1]+1, res.end());
}
return res;
}
};
其他的解法参考使用栈
使用stack存储每一个单词
pos指向第一个不是’ '的位置,即单词的首字母
将pos所指的单词保存到stack中
最后将stack中的单词保存到字符串中
class Solution {
public:
string reverseWords(string s) {
stack<string> st;
int pos = 0;
while (true) {
pos = s.find_first_not_of(' ', pos); // 指向单词首字母
if (pos == string::npos)
break;
st.push(s.substr(pos, s.find(' ', pos) - pos)); // 储存单词
pos = s.find(' ', pos); // 找到单词后的位置
}
string out;
while (!st.empty()) {
out += st.top() + " ";
st.pop();
}
out.pop_back(); //删除多余空格
return out;
}
};
//作者:da-ge-he-cha
反转字符串中的单词 III
给定一个字符串,你需要反转字符串中每个单词的字符顺序,同时仍保留空格和单词的初始顺序。
注意:在字符串中,每个单词由单个空格分隔,并且字符串中不会有任何额外的空格。
class Solution {
public:
string reverseWords(string s) {
s.append(" ");
for(int i = 0, begin = 0, end = 0; i < s.length(); i++) {
if(s[i] == ' ') {
end = i - 1;
while(begin < end)
swap(s[begin++], s[end--]);
begin = i + 1;
}
}
s.pop_back();
return s;
}
};
//作者:yoniga


























 785
785

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








