打卡信奥刷题（2518）用C++实现信奥 P1966 [NOIP 2013 提高组] 火柴排队

P1966 [NOIP 2013 提高组] 火柴排队

题目背景

NOIP2013 提高组 D1T2

题目描述

涵涵有两盒火柴，每盒装有 $n$ 根火柴，每根火柴都有一个高度。 现在将每盒中的火柴各自排成一列， 同一列火柴的高度互不相同， 两列火柴之间的距离定义为：$ \sum (a_i-b_i)^2$。

其中 $a_i$ 表示第一列火柴中第 $i$ 个火柴的高度，$b_i$ 表示第二列火柴中第 $i$ 个火柴的高度。

每列火柴中相邻两根火柴的位置都可以交换，请你通过交换使得两列火柴之间的距离最小。请问得到这个最小的距离，最少需要交换多少次？如果这个数字太大，请输出这个最小交换次数对 $10^8-3$ 取模的结果。

输入格式

共三行，第一行包含一个整数 $n$，表示每盒中火柴的数目。

第二行有 $n$ 个整数，每两个整数之间用一个空格隔开，表示第一列火柴的高度。

第三行有 $n$ 个整数，每两个整数之间用一个空格隔开，表示第二列火柴的高度。

输出格式

一个整数，表示最少交换次数对 $10^8-3$ 取模的结果。

输入输出样例 #1

输入 #1

4
2 3 1 4
3 2 1 4

输出 #1

1

输入输出样例 #2

输入 #2

4
1 3 4 2
1 7 2 4

输出 #2

2

说明/提示

输入输出样例说明一

最小距离是 $ 0$，最少需要交换 $1$ 次，比如：交换第 $1 $ 列的前 $ 2$ 根火柴或者交换第 $2$ 列的前 $2 $ 根火柴。

输入输出样例说明二

最小距离是 $10$，最少需要交换 $2$ 次，比如：交换第 $1$ 列的中间 $2$ 根火柴的位置，再交换第 $2$ 列中后 $2$ 根火柴的位置。

数据范围

对于 $10\%$ 的数据， $1\le n\le 10$；

对于 $30\%$ 的数据，$1\le n\le 100$；

对于 $60\%$ 的数据，$1\le n\le 10^3$；

对于 $100\%$ 的数据，$1\le n\le 10^5$，$0\le a_i,b_i<2^{31}$ 且对于任意 $1\le i<j\le n$，$a_i\ne a_j$，$b_i\ne b_j$。

C++实现

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100005,mod=99999997;

int A[N],B[N],a[N],b[N],l[N],c[5*N];
ll ans;
int n;

void add(int x,int y){
	for(;x<=n;x+=x&-x) c[x]+=y;
}

int ask(int x){
	ll ans=0;
	for(;x;x-=x&-x) ans+=c[x];
	return ans;
}

bool cmp1(int i,int j){
	return A[i]<A[j];
}

bool cmp2(int i,int j){
	return B[i]<B[j];
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i) scanf("%d",&A[i]),a[i]=i;
	for(int i=1;i<=n;++i) scanf("%d",&B[i]),b[i]=i;
	sort(a+1,a+1+n),sort(b+1,b+1+n);//离散化
	sort(a+1,a+1+n,cmp1),sort(b+1,b+1+n,cmp2);
	for(int i=1;i<=n;++i) l[a[i]]=b[i];
	for(int i=n;i;i--){//树状数组求逆序对
		ans=(ans+ask(l[i]-1))%mod;
		add(l[i],1);	
	}
	printf("%lld",ans%mod);
	return 0;
}

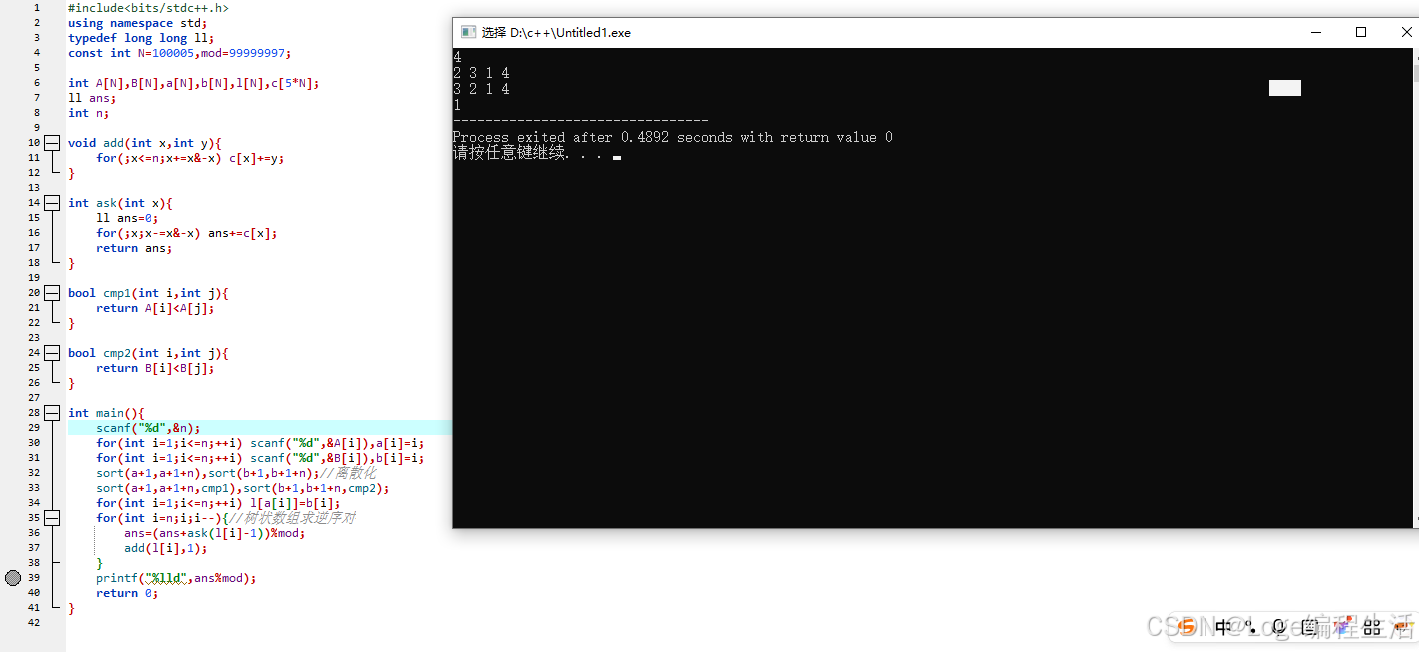
后续

接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现，记录日常的编程生活、比赛心得，感兴趣的请关注，我后续将继续分享相关内容